Rambler's Top100Astronet    
  po tekstam   po klyuchevym slovam   v glossarii   po saitam   perevod   po katalogu 		 

Mehanika tverdogo tela. Lekcii.

V.A.Aleshkevich, L.G.Dedenko, V.A.Karavaev (Fizicheskii fakul'tet MGU)
Izdatel'stvo Fizicheskogo fakul'teta MGU, 1997 g. Soderzhanie

Primer 2. Pri kilevoi kachke korablya (s nosa na kormu i obratno) rotor bystrohodnoi turbiny uchastvuet v dvuh dvizheniyah: vo vrashenii vokrug svoei osi s uglovoi skorost'yu $\omega$ i v povorote vokrug gorizontal'noi osi, perpendikulyarnoi valu turbiny, s uglovoi skorost'yu $\Omega$ (ris. 4.13). Pri etom val turbiny budet davit' na podshipniki s silami ${\displaystyle \bf F}\div {\displaystyle \bf F'},$ lezhashimi v gorizontal'noi ploskosti. Pri kachke eti sily, kak i giroskopicheskii moment, periodicheski menyayut svoe napravlenie na protivopolozhnoe i mogut vyzvat' "ryskanie" korablya, esli on ne slishkom velik (naprimer, buksira).

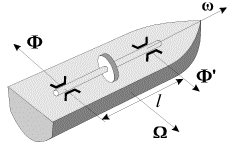Ris. 4.13.

Dopustim, chto massa turbiny $m = 3000 kg,$ ee radius inercii $R_{in} = 0,5 m,$ skorost' vrasheniya turbiny $n = 3000 ob/min,$ maksimal'naya uglovaya skorost' korpusa sudna pri kilevoi kachke $\Omega = 5 grad/s,$ rasstoyanie mezhdu podshipnikami $\ell = 2 m.$ Maksimal'noe znachenie giroskopicheskoi sily, deistvuyushei na kazhdyi iz podshipnikov, sostavlyaet

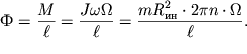$ F = {\displaystyle \frac{\displaystyle {\displaystyle M}}{\displaystyle {\displaystyle \ell }}} = {\displaystyle \frac{\displaystyle {\displaystyle J\omega \Omega }}{\displaystyle {\displaystyle \ell }}} = {\displaystyle \frac{\displaystyle {\displaystyle mR_{in}^{2} \cdot 2\pi n \cdot \Omega }}{\displaystyle {\displaystyle \ell }}}. $(4.19)

Posle podstanovki chislovyh dannyh poluchim $F \approx 10^{4} H,$ to est' okolo 1 tonny.

Primer 3. Giroskopicheskie sily mogut vyzvat' tak nazyvaemye kolebaniya "shimmi" koles avtomobilya (ris. 4.14) [V.A. Pavlov, 1985]. Kolesu, vrashayushemusya vokrug osi AA' s uglovoi skorost'yu $\omega ,$ v moment naezda na prepyatstvie soobshaetsya dopolnitel'naya skorost' vynuzhdennogo povorota vokrug osi, perpendikulyarnoi ploskosti risunka. Pri etom voznikaet moment giroskopicheskih sil, i koleso nachnet povorachivat'sya vokrug osi BB'. Priobretaya uglovuyu skorost' povorota vokrug osi BB', koleso snova nachnet povorachivat'sya vokrug osi, perpendikulyarnoi ploskosti risunka, deformiruya uprugie elementy podveski i vyzyvaya sily, stremyashiesya vernut' koleso v prezhnee vertikal'noe polozhenie. Dalee situaciya povtoryaetsya. Esli v konstrukcii avtomobilya ne prinyat' special'nyh mer, voznikshie kolebaniya "shimmi" mogut privesti k sryvu pokryshki s oboda kolesa i k polomke detalei ego krepleniya.

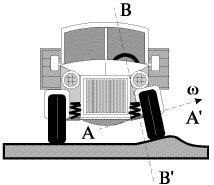Ris. 4.14.

Primer 4. S giroskopicheskim effektom my stalkivaemsya i pri ezde na velosipede (ris. 4.15). Sovershaya, naprimer, povorot napravo, velosipedist instinktivno smeshaet centr tyazhesti svoego tela vpravo, kak by zavalivaya velosiped. Voznikshee prinuditel'noe vrashenie velosipeda s uglovoi skorost'yu $\Omega$ privodit k poyavleniyu giroskopicheskih sil s momentom ${\displaystyle \bf {\displaystyle M}'}$ Na zadnem kolese etot moment budet pogashen v podshipnikah, zhestko svyazannyh s ramoi. Perednee zhe koleso, imeyushee po otnosheniyu k rame svobodu vrasheniya v rulevoi kolonke, pod deistviem giroskopicheskogo momenta nachnet povorachivat'sya kak raz v tom napravlenii, kotoroe bylo neobhodimo dlya pravogo povorota velosipeda. Opytnye velosipedisty sovershayut podobnye povoroty, chto nazyvaetsya, "bez ruk".

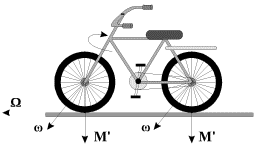Ris. 4.15.

Vopros o vozniknovenii giroskopicheskih sil mozhno rassmatrivat' i s drugoi tochki zreniya. Mozhno schitat', chto giroskop, izobrazhennyi na ris. 4.10, uchastvuet v dvuh odnovremennyh dvizheniyah: otnositel'nom vrashenii vokrug sobstvennoi osi s uglovoi skorost'yu $\omega$ i perenosnom, vynuzhdennom povorote vokrug vertikal'noi osi s uglovoi skorost'yu $\Omega .$ Takim obrazom, elementarnye massy $\Delta m_{i} ,$ na kotorye mozhno razbit' disk giroskopa (malen'kie kruzhki na ris. 4.16), dolzhny ispytyvat' koriolisovy uskoreniya

$ {\displaystyle \bf a}_{i kor} = 2 \Omega\times {\displaystyle \bf v}_{i otn} . $(4.20)

Eti uskoreniya budut maksimal'ny dlya mass, nahodyashihsya v dannyi moment vremeni na vertikal'nom diametre diska, i ravny nulyu dlya mass, kotorye nahodyatsya na gorizontal'nom diametre (ris. 4.16).

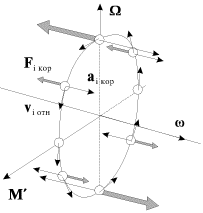Ris. 4.16.

V sisteme otscheta, vrashayusheisya s uglovoi skorost'yu $\Omega$ (v etoi sisteme otscheta os' giroskopa nepodvizhna), na massy $\Delta m_{i}$ budut deistvovat' koriolisovy sily inercii

$ F_{i kor} = 2\Delta m_{i} {\displaystyle \bf v}_{otn} \times \Omega $(4.21)

Eti sily sozdayut moment ${\displaystyle \bf {\displaystyle M}'},$ kotoryi stremitsya povernut' os' giroskopa takim obrazom, chtoby vektor \omega sovmestilsya s $\omega.$ Moment ${\displaystyle \bf {\displaystyle M}'}$ dolzhen byt' uravnoveshen momentom sil reakcii ${\displaystyle \bf F}\div {\displaystyle \bf {\displaystyle F}'},$ deistvuyushih na os' giroskopa so storony podshipnikov. Po tret'emu zakonu N'yutona, os' budet deistvovat' na podshipniki, a cherez nih i na ramu, v kotoroi eta os' zakreplena, s giroskopicheskimi silami ${\displaystyle \bf F}\div {\displaystyle \bf F'}.$ Poetomu i govoryat, chto giroskopicheskie sily obuslovleny silami Koriolisa.

Vozniknovenie koriolisovyh sil mozhno legko prodemonstrirovat', esli vmesto zhestkogo diska (ris. 4.16) vzyat' gibkii rezinovyi lepestok (ris. 4.17). Pri povorote vala s raskruchennym lepestkom vokrug vertikal'noi osi lepestok izgibaetsya pri prohozhdenii cherez vertikal'noe polozhenie tak, kak izobrazheno na ris. 4.17.

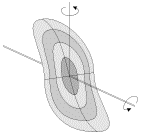Ris. 4.17.

Volchki.

Volchki kardinal'no otlichayutsya ot giroskopov tem, chto v obshem sluchae oni ne imeyut ni odnoi nepodvizhnoi tochki. Proizvol'noe dvizhenie volchkov imeet ves'ma slozhnyi harakter: buduchi raskrucheny vokrug osi simmetrii i postavleny na ploskost', oni precessiruyut, "begayut" po ploskosti, vypisyvaya zamyslovatye figury, a inogda dazhe perevorachivayutsya s odnogo konca na drugoi. Ne vdavayas' v detali takogo neobychnogo povedeniya volchkov, otmetim lish', chto nemalovazhnuyu rol' zdes' igraet sila treniya, voznikayushaya v tochke soprikosnoveniya volchka i ploskosti.

Kratko ostanovimsya na voprose ob ustoichivosti vrasheniya simmetrichnogo volchka proizvol'noi formy. Opyt pokazyvaet, chto esli simmetrichnyi volchok privesti vo vrashenie vokrug osi simmetrii i ustanovit' na ploskost' v vertikal'nom polozhenii, to eto vrashenie v zavisimosti ot formy volchka i uglovoi skorosti vrasheniya budet libo ustoichivym, libo neustoichivym.

Pust' imeetsya simmetrichnyi volchok, izobrazhennyi na ris. 4.18. Vvedem sleduyushie oboznacheniya: O - centr mass volchka, $h$ - rasstoyanie ot centra mass do tochki opory; K - centr krivizny volchka v tochke opory, $r$ - radius krivizny; $J_{z}$ - moment inercii otnositel'no osi simmetrii, $J_{x}$ - moment inercii otnositel'no glavnoi central'noi osi, perpendikulyarnoi osi simmetrii.

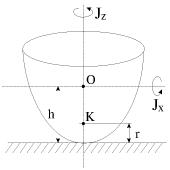Ris. 4.18.

Analiz ustoichivosti vrasheniya volchka privodit k diagramme, izobrazhennoi na ris. 4.19. Zdes' po osi absciss otlozheno otnoshenie ${\displaystyle \frac{\displaystyle {\displaystyle J_{z} }}{\displaystyle {\displaystyle J_{x} }}},$ a po osi ordinat - otnoshenie ${\displaystyle \frac{\displaystyle {\displaystyle h}}{\displaystyle {\displaystyle r}}}.$

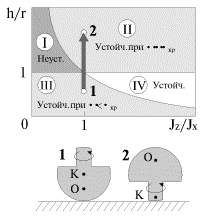Ris. 4.19.

Provedem giperbolu ${\displaystyle \frac{\displaystyle {\displaystyle h}}{\displaystyle {\displaystyle r}}} = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle J_{z} / J_{x} }}}$ i pryamuyu ${\displaystyle \frac{\displaystyle {\displaystyle h}}{\displaystyle {\displaystyle r}}} = 1.$ Eti linii delyat oblast' polozhitel'nyh znachenii ${\displaystyle \frac{\displaystyle {\displaystyle h}}{\displaystyle {\displaystyle r}}}, {\displaystyle \frac{\displaystyle {\displaystyle J_{z} }}{\displaystyle {\displaystyle J_{x} }}}$ na 4 chasti.

Oblast' I sootvetstvuet neustoichivomu vrasheniyu volchka pri vseh uglovyh skorostyah, oblast' II - ustoichivomu vrasheniyu pri dostatochno bol'shih uglovyh skorostyah $\omega \gt \omega _{kr} .$ Oblast' III sootvetstvuet ustoichivomu vrasheniyu pri malyh uglovyh skorostyah $\omega \lt \omega _{kr} ,$ oblast' IV - ustoichivomu vrasheniyu pri proizvol'nyh $\omega .$Kriticheskaya uglovaya skorost' $\omega_{kr}$zavisit ot momentov inercii $J_z, J_y,$ rasstoyanii $r, h$ i vesa tela $P=mg$[K. Magnus, 1974]:

$ \omega_{kr}^2=\frac{\displaystyle (h-r)\cdot P}{\displaystyle J_x (r/h)\cdot (J_z /J_x - r/h)} $(4.22)

Rassmotrim, naprimer, kitaiskii volchok, raskruchennyi do $\omega \gt \omega _{kr} ,$ i postavlennyi na ploskost' vertikal'no, kak pokazano na ris. 4.20a. Pust' $J_{z} = J_{x} .$ Poskol'ku $h \lt r,$ to etoi situacii sootvetstvuet tochka 1 v oblasti III na ris. 4.19, to est' oblast' ustoichivogo vrasheniya lish' pri malyh $\omega .$ Takim obrazom, v nashem sluchae $\left( {\displaystyle \omega \gt \omega _{kr} } \right)$ vrashenie budet neustoichivym, i volchok perevernetsya na nozhku (tochka 2 v oblasti II na ris. 4.19).

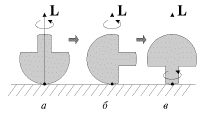Ris. 4.20.

Sleduet obratit' vnimanie, chto v processe perevorachivaniya volchka rezul'tiruyushii moment impul'sa sohranyaet svoe pervonachal'noe napravlenie, to est' vektor L, vse vremya napravlen vertikal'no vverh. Eto oznachaet, chto v situacii, izobrazhennoi na ris. 4.20b, kogda os' volchka gorizontal'na, vrashenie vokrug osi simmetrii volchka otsutstvuet! Dalee, pri oprokidyvanii na nozhku, vrashenie vokrug osi simmetrii budet protivopolozhno ishodnomu (esli smotret' vse vremya so storony nozhki, ris. 4.20v).

V sluchae yaiceobraznogo volchka poverhnost' tela v okrestnosti tochki opory ne yavlyaetsya sferoi, no sushestvuyut dva vzaimno perpendikulyarnyh napravleniya, dlya kotoryh radius krivizny v tochke opory prinimaet ekstremal'nye (minimal'noe i maksimal'noe) znacheniya. Opyty pokazyvayut, chto v sluchae, izobrazhennom na ris. 4.21a, vrashenie budet neustoichivym, i volchok prinimaet vertikal'noe polozhenie, raskruchivayas' vokrug osi simmetrii i prodolzhaya ustoichivoe vrashenie na bolee ostrom konce. Eto vrashenie budet prodolzhat'sya do teh por, poka sily treniya ne pogasyat v dostatochnoi mere kineticheskuyu energiyu volchka, uglovaya skorost' umen'shitsya (stanet men'she $\omega _{0}$ ), i volchok upadet.

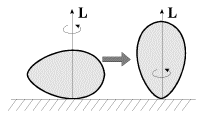Ris. 4.21.

Literatura

  1. A.N. Matveev. Mehanika i teoriya otnositel'nosti. M.: Vysshaya shkola, 1986.
  2. S.P. Strelkov. Mehanika. M.: Nauka, 1975.
  3. S.E. Haikin. Fizicheskie osnovy mehaniki. M.: Nauka, 1971.
  4. D.V. Sivuhin. Obshii kurs fiziki. T.1. Mehanika. M.: Nauka, 1989.
  5. R.V. Pol'. Mehanika, akustika i uchenie o teplote. M.: Nauka, 1971.
  6. R. Feinman i dr. Feinmanovskie lekcii po fizike. M.: Mir, 1977.
  7. Ch. Kittel', U. Nait, M. Ruderman. Mehanika. M.: Nauka, 1983.
  8. K. Magnus. Giroskop. Teoriya i primenenie. M., 1974.
  9. V.A. Pavlov. Giroskopicheskii effekt, ego proyavleniya i ispol'zovanie. L., 1985.

Nazad

Publikacii s klyuchevymi slovami: mehanika - tverdoe telo - ugly Eilera
Publikacii so slovami: mehanika - tverdoe telo - ugly Eilera
Sm. takzhe:

Mneniya chitatelei [2]
Ocenka: 3.2 [golosov: 188]
 
O reitinge
Versiya dlya pechati Raspechatat'

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

Astronet | Nauchnaya set' | GAISh MGU | Poisk po MGU | O proekte | Avtoram

Kommentarii, voprosy? Pishite: info@astronet.ru ili syuda

Rambler's Top100 Yandeks citirovaniya