Astronet > Mehanika tverdogo tela. Lekcii.

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Mehanika tverdogo tela. Lekcii.

V.A.Aleshkevich, L.G.Dedenko, V.A.Karavaev (Fizicheskii fakul'tet MGU)
Izdatel'stvo Fizicheskogo fakul'teta MGU, 1997 g. Soderzhanie

Ploskoe dvizhenie.

Ploskoe dvizhenie - eto takoe dvizhenie tverdogo tela, pri kotorom traektorii vseh ego tochek lezhat v parallel'nyh ploskostyah. Esli v tele provesti nekotoruyu pryamuyu O₁O₂, perpendikulyarnuyu etim ploskostyam (ris. 1.9), to vse tochki etoi pryamoi budut dvigat'sya po odinakovym traektoriyam s odinakovymi skorostyami i uskoreniyami; sama pryamaya budet, estestvenno, sohranyat' svoyu orientaciyu v prostranstve. Takim obrazom, pri ploskom, ili, kak ego inogda nazyvayut, plosko-parallel'nom, dvizhenii tverdogo tela dostatochno rassmotret' dvizhenie odnogo iz sechenii tela.

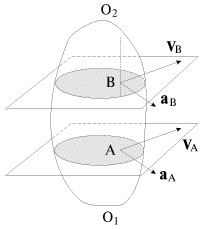Ris. 1.9.

Obratimsya k klassicheskomu prostomu primeru ploskogo dvizheniya - kacheniyu cilindra po ploskosti bez proskal'zyvaniya. Rassmatrivaya odno iz sechenii cilindra ploskost'yu, perpendikulyarnoi ego osi, my pridem k izvestnoe zadache o katyashemsya kolese (ris. 1.10). Centr kolesa dvizhetsya pryamolineino, traektorii drugih tochek predstavlyayut soboi krivye, nazyvaemye cikloidami.

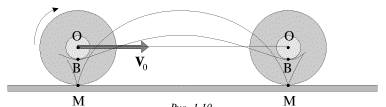Ris. 1.10.

Pri otsutstvii proskal'zyvaniya mgnovennaya skorost' samoi nizhnei tochki kolesa (tochki M) ravna nulyu. Eto pozvolyaet rassmatrivat' kachenie kolesa kak superpoziciyu dvuh dvizhenii: postupatel'nogo so skorost'yu osi $v_{0}$ i vrashatel'nogo s uglovoi skorost'yu $\omega = {\displaystyle \frac{\displaystyle {\displaystyle v_{0} }}{\displaystyle {\displaystyle R}}},$ gde $R$ - radius kolesa. Yasno, chto v etom sluchae $v_{M} = v_{0} - \omega R = 0.$

Poprobuem obobshit' etot priem na proizvol'noe ploskoe dvizhenie.

Vydelim otrezok AB v rassmatrivaemom sechenii tverdogo tela (ris. 1.11). Perevod secheniya iz polozheniya 1 v polozhenie 2 mozhno rassmatrivat' kak superpoziciyu dvuh dvizhenii: postupatel'nogo iz 1 v 1' i vrashatel'nogo iz 1' v 2 vokrug tochki A', nazyvaemoi obychno polyusom (ris. 1.11a). Sushestvenno, chto v kachestve polyusa mozhno vybrat' lyubuyu tochku, prinadlezhashuyu secheniyu ili dazhe lezhashuyu v ploskosti sechenie vne ego. Na ris. 1.11b, k primeru, v kachestve polyusa vybrana tochka V. Obratite vnimanie: dlina puti pri postupatel'nom peremeshenii izmenilas' (v dannom sluchae uvelichilas'), no ugol povorota ostalsya prezhnim!

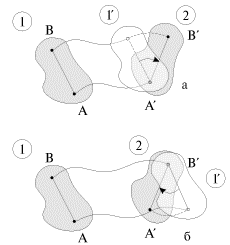Ris. 1.11.

Priblizhaya konechnoe polozhenie tela k nachal'nomu (sokrashaya rassmatrivaemyi promezhutok vremeni), prihodim k vyvodu: ploskoe dvizhenie tverdogo tela v lyuboi moment vremeni mozhno predstavit' kak superpoziciyu postupatel'nogo dvizheniya so skorost'yu nekotoroi tochki, vybrannoi v kachestve polyusa, i vrasheniya vokrug osi, prohodyashei cherez polyus. V real'noi situacii oba eti dvizheniya, estestvenno, proishodyat odnovremenno. Sushestvenno, chto razlozhenie na postupatel'noe i vrashatel'noe dvizheniya okazyvaetsya neodnoznachnym, prichem v zavisimosti ot vybora polyusa skorost' postupatel'nogo dvizheniya budet izmenyat'sya, a uglovaya skorost' vrasheniya ostanetsya neizmennoi.

V sootvetstvii so skazannym skorost' lyuboi tochki A tela (ris. 1.12) geometricheski skladyvaetsya iz skorosti kakoi-libo drugoi tochki O, prinyatoi za polyus, i skorosti vrashatel'nogo dvizheniya vokrug etogo polyusa. Napomnim, chto sistema koordinat XYZ na ris. 1.12 - nepodvizhnaya (laboratornaya); nachalo sistemy x₀y₀z₀ pomesheno v nekotoruyu tochku O tela (polyus), a sama sistema x₀y₀z₀ dvizhetsya otnositel'no XYZ postupatel'no, prichem tak, chto osi Oy₀ i Oz₀ ostayutsya v ploskosti risunka. Rassmatrivaemaya tochka A tela takzhe dvizhetsya v ploskosti risunka (ploskoe dvizhenie!).

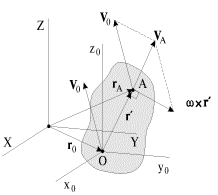Ris. 1.12.

Radius-vektor tochki A

${\displaystyle \bf r}_{A} = {\displaystyle \bf r}_{0} + {\displaystyle {\displaystyle \bf r}}'$

(1.15)

Skorost' tochki A

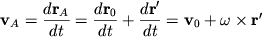${\displaystyle \bf v}_{A} = {\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle \bf r}_{A} }}{\displaystyle {\displaystyle dt}}} = {\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle \bf r}_{0} }}{\displaystyle {\displaystyle dt}}} + {\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle {\displaystyle \bf r}}'}}{\displaystyle {\displaystyle dt}}} = {\displaystyle \bf v}_{0} + \omega\times {\displaystyle {\displaystyle \bf r}}'$

(1.16)

Iz (1.16) mozhno sdelat' vyvod, chto v lyuboi moment vremeni dolzhna sushestvovat' takaya tochka M, skorost' kotoroi v laboratornoi sisteme XYZ ravna nulyu - dlya etoi tochki

${\displaystyle \bf v}_{0} = - \omega\times {\displaystyle {\displaystyle \bf r}}'$

(1.17)

(ris. 1.13). Zametim, chto eta tochka ne obyazatel'no dolzhna prinadlezhat' telu, to est' mozhet nahodit'sya i vne ego. Takim obrazom, ploskoe dvizhenie tverdogo tela v dannyi moment vremeni mozhno predstavit' kak chistoe vrashenie vokrug osi, prohodyashei cherez tochku M - takaya os' nazyvaetsya obychno mgnovennoi os'yu vrasheniya. V chastnosti, dlya kolesa, katyashegosya po ploskosti bez proskal'zyvaniya (ris. 1.10), mgnovennaya os' vrasheniya prohodit cherez tochku M soprikosnoveniya kolesa s ploskost'yu.

Ris. 1.13.

Sushestvenno, chto v raznye momenty vremeni mgnovennaya os' vrasheniya prohodit cherez raznye tochki tverdogo tela i cherez raznye tochki laboratornoi sistemy XYZ, sohranyaya, konechno, svoyu orientaciyu v prostranstve.

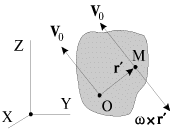
Dlya togo, chtoby opredelit' polozhenie mgnovennoi osi vrasheniya, neobhodimo znat' skorosti kakih-libo dvuh tochek tverdogo tela. Tak, na ris. 1.14 pokazano polozhenie mgnovennoi osi vrasheniya (tochka M) dlya cilindra, zazhatogo mezhdu dvumya parallel'nymi reikami, kotorye dvizhutsya v odnu i tu zhe storonu s raznymi skorostyami $\bf v}_{1$ i ${\displaystyle \bf v}_{2}.$

Ris. 1.14.

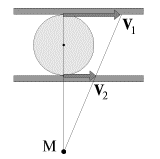
V situacii, izobrazhennoi na ris. 1.15, sterzhen' AB opiraetsya na tochku S i dvizhetsya v ploskosti chertezha tak, chto ego konec B vse vremya nahoditsya na poluokruzhnosti CBD Pri etom mgnovennaya os' vrasheniya sterzhnya (tochka M) nahoditsya na verhnei poluokruzhnosti CMD i pri dvizhenii tochki B vpravo peremeshaetsya po duge etoi poluokruzhnosti vlevo.

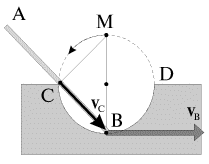Ris. 1.15.

V sluchae, pokazannom na ris. 1.16, sterzhen', opirayushiisya odnim iz svoih koncov na gladkuyu gorizontal'nuyu ploskost', nachinaet padat' iz vertikal'nogo polozheniya. Pri etom centr mass sterzhnya opuskaetsya, ostavayas' na odnoi i toi zhe vertikali. Mgnovennaya os' vrasheniya (tochka M) peremeshaetsya po duge okruzhnosti radiusa $\frac{\displaystyle {\displaystyle \ell }}{\displaystyle {\displaystyle 2}}$ ( $\ell$ - dlina sterzhnya).

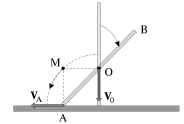Ris. 1.16.

Znaya uglovuyu skorost' $\omega$ i polozhenie mgnovennoi osi vrasheniya, mozhno legko opredelit' skorost' lyuboi tochki tela pri ego ploskom dvizhenii. Tak, v sluchae kolesa, katyashegosya po ploskosti so skorost'yu $v_{0}$ bez proskal'zyvaniya (ris. 1.17), skorost' tochki V

$v_{B} = \omega \cdot MB = {\displaystyle \frac{\displaystyle {\displaystyle v_{0} }}{\displaystyle {\displaystyle R}}} \cdot MB;$

(1.18)

vektor $\bf v}_{B$ perpendikulyaren otrezku v MV, soedinyayushemu tochku V s tochkoi M, cherez kotoruyu prohodit mgnovennaya os' vrasheniya. Estestvenno, $\bf v}_{B$ mozhno predstavit' i kak geometricheskuyu summu dvuh skorostei: $\bf v}_{0$ - skorosti postupatel'nogo dvizheniya osi kolesa i ${\displaystyle \bf v}}'_{0$ - skorosti vrashatel'nogo dvizheniya vokrug etoi osi, prichem ${\displaystyle \left| {\displaystyle {\displaystyle \bf v}_{0} } \right|} = {\displaystyle \left| {\displaystyle {\displaystyle {\displaystyle \bf v}}'_{0} } \right|}.$ (ris. 1.17).

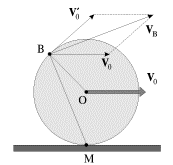Ris. 1.17.

Ris. 1.18 illyustriruet raspredelenie skorostei na vertikal'nom diametre kolesa zheleznodorozhnogo vagona. Mgnovennaya os' vrasheniya prohodit cherez tochku M soprikosnoveniya kolesa s rel'som. Horosho vidno, chto lineinaya skorost' tochki na krayu rebordy napravlena v storonu, protivopolozhnuyu dvizheniyu vagona.

Ris. 1.18.

Opredelim teper' uskoreniya tochek tela pri ploskom dvizhenii. Differenciruya vyrazheniem (1.16) po vremeni, poluchim dlya uskoreniya tochki A

$\bf a}_{A} = {\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle \bf v}_{A} }}{\displaystyle {\displaystyle dt}}} = {\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle \bf v}_{0} }}{\displaystyle {\displaystyle dt}}} + {\displaystyle \frac{\displaystyle {\displaystyle d\omega}}{\displaystyle {\displaystyle dt}}}\times {\displaystyle {\displaystyle \bf r}}' + \omega\times {\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle {\displaystyle \bf r}}'}}{\displaystyle {\displaystyle dt}}} = {\displaystyle \bf a}_{0} + {\displaystyle \bf a}_{\tau } + {\displaystyle \bf a}_{n$

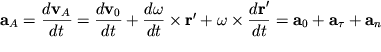(1.19)

Eto uskorenie skladyvaetsya iz treh chastot (ris. 1.19): uskoreniya $\bf a}_{0$ tochki O, prinyatoi za polyus, tangencial'nogo uskoreniya

${\displaystyle \bf a}_{\tau} = {\displaystyle \frac{\displaystyle {\displaystyle d\omega}}{\displaystyle {\displaystyle dt}}}\times {\displaystyle {\displaystyle \bf r}}' = \varepsilon\times {\displaystyle {\displaystyle \bf r}}'$

(1.20)

i normal'nogo uskoreniya

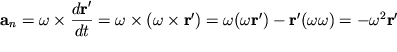${\displaystyle \bf a}_{n} = \omega\times {\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle {\displaystyle \bf r}}'}}{\displaystyle {\displaystyle dt}}} = \omega\times (\omega\times {\displaystyle {\displaystyle \bf r}}') = \omega (\omega {\displaystyle {\displaystyle \bf r}}') - {\displaystyle {\displaystyle \bf r}}'(\omega \omega) = - \omega ^{2}{\displaystyle {\displaystyle \bf r}}'$

(1.21)

(skalyarnoe proizvedenie $(\omega {\displaystyle r}')$ ravno nulyu, tak kak $\omega \bot {\displaystyle {\displaystyle \bf r}}'$ ).

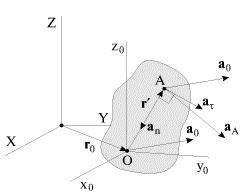Ris. 1.19.

Takim obrazom, uskorenie lyuboi tochki A tela pri ploskom dvizhenii ravno geometricheskoi summe uskoreniya tochki, prinyatoi za polyus, i uskoreniya tochk, prinyatoi za polyus, i uskoreniya tochki A za schet ee vrasheniya vokrug etogo polyusa. Otsyuda, v chastnosti, sleduet, chto uskorenie lyuboi tochki kolesa, katyashegosya bez proskal'zyvaniya po ploskosti s postoyannoi skorost'yu $v_{0}$ , napravleno k centru kolesa i ravno ${\displaystyle \frac{\displaystyle {\displaystyle v_{0} ^{2}}}{\displaystyle {\displaystyle r}}},$ gde $r$ - rasstoyanie rassmatrivaemoi tochki do centra kolesa. 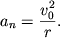V etom primere v kachestve polyusa udobno vybrat' centr kolesa O, togda $a_{0} = a_{\tau } = 0,$ i ostaetsya tol'ko $a_{n} = {\displaystyle \frac{\displaystyle {\displaystyle v_{0} ^{2}}}{\displaystyle {\displaystyle r}}}.$

Zamechanie. Po analogii s mgnovennoi os'yu vrasheniya mozhno vvesti mgnovennuyu os', uskoreniya vseh tochek kotoroi v dannyi moment vremeni ravny nulyu. Pri etom sleduet imet' v vidu, chto eta os', voobshe govorya, ne sovpadaet s mgnovennoi os'yu vrasheniya. Tak, v primere s kolesom, katyashimsya po ploskosti s postoyannoi skorost'yu, ona prohodit cherez centr kolesa.

Nazad| Vpered

Publikacii s klyuchevymi slovami: mehanika - tverdoe telo - ugly Eilera Publikacii so slovami: mehanika - tverdoe telo - ugly Eilera
Sm. takzhe: Mehanika sploshnyh sred Variacionnye principy mehaniki Anizotropiya

Mneniya chitatelei [2]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce