Astronet > Mehanika tverdogo tela. Lekcii.

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Mehanika tverdogo tela. Lekcii.

V.A.Aleshkevich, L.G.Dedenko, V.A.Karavaev (Fizicheskii fakul'tet MGU)
Izdatel'stvo Fizicheskogo fakul'teta MGU, 1997 g. Soderzhanie

Dvizhenie tverdogo tela s odnoi nepodvizhnoi tochkoi.

Primery takih tel pokazany na ris. 1.20: volchok s sharnirno zakreplennym ostriem (a), konus, katayushiisya po ploskosti bez proskal'zyvaniya (b). V etom sluchae telo imeet tri stepeni svobody - nachala sistem XYZ i x₀y₀z₀, vvedennyh v nachale lekcii, mozhno sovmestit' s tochkoi zakrepleniya, a dlya opisaniya dvizheniya tela ispol'zovat' tri ugla Eilera:

$\varphi = \varphi (t); \psi = \psi (t); \theta = \theta (t).$

(1.22)

Dlya tverdogo uela s odnoi nepodvizhnoi tochkoi spravedliva teorema Eilera: tverdoe telo, zakreplennoe v odnoi tochke, mozhet byt' perevedeno iz odnogo polozheniya v lyuboe drugoe odnim povorotom na nekotoryi ugol vokrug nepodvizhnoi osi, prohodyashei cherez tochku zakrepleniya. Dokazatel'stvo etoi teoremy mozhno naiti v uchebnikah. Dlya nas vazhno sledstvie iz etoi teoremy: dvizhenie zakreplennogo v tochke tverdogo tela v kazhdyi moment vremeni mozhno rassmatrivat' kak vrashenie vokrug mgnovennoi osi, prohodyashei cherez tochku zakrepleniya. Estestvenno, chto polozhenie etoi osi kak v prostranstve, tak i otnositel'no samogo tela s techeniem vremeni v obshem sluchae menyaetsya.

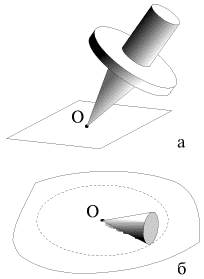Ris. 1.20.

Geometricheskoe mesto polozhenii mgnovennoi osi vrasheniya otnositel'no nepodvizhnoe sistemy XYZ (ili x₀y₀z₀) - eto slozhnaya konicheskaya poverhnost' s vershinoi v tochke zakrepleniya. V teoreticheskoi mehanike ee nazyvayut nepodvizhnym aksoidom. Geometricheskoe mesto polozhenii mgnovennoi osi vrasheniya otnositel'no podvyazhis' sistemy xyz, zhestko svyazannoi s tverdym telom, - eto tozhe konicheskaya poverhnost' - podvizhnyi aksoid. Naprimer, v sluchae konusa AO₁, katyashegosya po poverhnosti drugogo konusa AO₂ bez proskal'zyvaniya (ris. 1.21; tochka A podvizhnogo konusa sharnirno zakreplena) nepodvizhnyi aksoid sovpadaet s poverhnost'yu nepodvizhnogo konusa AO₂, a podvizhnyi aksoid - s poverhnost'yu podvizhnogo konusa AO₁.

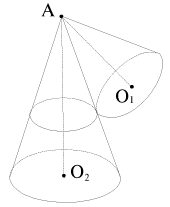Ris. 1.21.

Skorost' proizvol'noi tochki tverdogo tela mozhno rasschitat' kak lineinuyu skorost' vrashatel'nogo dvizheniya vokrug mgnovennoi osi:

${\displaystyle \bf v} = \omega\times {\displaystyle \bf r},$

(1.23)

gde r - radius-vektor tochki otnositel'no nachala sistemy XYZ ili x₀y₀z₀, sovmeshennogo s tochkoi zakrepleniya. Sleduet tol'ko imet' v vidu, chto, v otlichie ot vrasheniya vokrug nepodvizhnoi osi, "plecho" vektora v (rasstoyanie rassmatrivaemoi tochki do mgnovennoi osi vrasheniya) yavlyaetsya funkciei vremeni.

Uskorenie proizvol'noi tochki tverdogo tela

$\bf a} = {\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle \bf v}}}{\displaystyle {\displaystyle dt}}} = {\displaystyle \frac{\displaystyle {\displaystyle d\omega}}{\displaystyle {\displaystyle dt}}}\times {\displaystyle \bf r} + \omega\times {\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle \bf r}}}{\displaystyle {\displaystyle dt}}$

(1.24)

sostoit iz dvuh chastei: uskoreniya, svyazannogo s neravnomernost'yu vrasheniya (izmeneniem $\omega$ po velichine)

$a_{vr} = {\displaystyle \frac{\displaystyle {\displaystyle d\omega}}{\displaystyle {\displaystyle dt}}}\times r = \varepsilon\times {\displaystyle \bf r},$

(1.25)

i centrostremitel'nogo (normal'nogo) uskoreniya

${\displaystyle \bf a}_{n} = \omega\times {\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle \bf r}}}{\displaystyle {\displaystyle dt}}} = \omega\times \left( {\displaystyle \omega\times {\displaystyle \bf r}} \right) = - \omega^{2}\rho,$

(1.26)

gde $\rho = \rho\left( {\displaystyle t} \right)$ - radius-vektor, provedennyi ot mgnovennoi osi vrasheniya v rassmatrivaemuyu tochku. Zdes' sleduet pomnit', chto uglovoe uskorenie $\varepsilon = {\displaystyle \frac{\displaystyle {\displaystyle d\omega}}{\displaystyle {\displaystyle dt}}}$ svyazano s izmeneniem uglovoi skorosti ne tol'ko po velichine, no i po napravleniyu, tak chto $\bf a}_{vr$ i $\bf a}_{n$ ne perpendikulyarny drug drugu.

Proekcii vektora mgnovennoi uglovoi skorosti $\omega$ na osi sistemy xyz, zhestko svyazannoi s tverdym telom, mozhno vyrazit' cherez ugly Eilera $\varphi , \psi , \theta$ (sm. Ris. 1.3) i ih proizvodnye po vremeni $\dot {\displaystyle \varphi }, \dot {\displaystyle \psi }, \dot {\displaystyle \theta }.$ Deistvitel'no, vektor $\omega$ mozhno predstavit' v vide summy treh sostavlyayushih:

$\omega = \dot {\displaystyle \varphi } {\displaystyle \bf e}_{z} + \dot {\displaystyle \psi } {\displaystyle \bf e}_{z_{o}} + \dot {\displaystyle \theta } {\displaystyle \bf e}_{OA} .$

(1.27)

Zdes' $\bf e}_{z$ i $\bf e}_{z_{0}$ - edinichnye vektory vdol' osei Oz i Oz₀ sootvetstvenno, $\bf e}_{OA$ - edinichnyi vektor vdol' linii uzlov OA (na ris. 1.3 eti orty ne pokazany). Opredelim proekcii vektorov $\dot {\displaystyle \varphi } {\displaystyle \bf e}_{z} , \dot {\displaystyle \psi } {\displaystyle \bf e}_{z_{o}} , \dot {\displaystyle \theta } {\displaystyle \bf e}_{OA},$ vhodyashih v (1.27), na osi sistemy xyz (sm. ris. 1.3):

$\left( \dot {\displaystyle \varphi } {\displaystyle \bf e}_{z} \right)_{x} = 0; \quad \left( \dot {\displaystyle \varphi } {\displaystyle \bf e}_{z} \right)_{y} = 0; \quad \left( \dot {\displaystyle \varphi } {\displaystyle \bf e}_{z} \right)_{z} = \dot {\displaystyle \varphi };$

(1.28)

$\left( {\displaystyle \dot {\displaystyle \psi }{\displaystyle \bf e}_{z_{0} } } \right)_{x} = \dot {\displaystyle \psi } \sin \theta \cdot \sin \varphi ; \quad \left( {\displaystyle \dot {\displaystyle \psi }{\displaystyle \bf e}_{z_{0} } } \right)_{y} = \dot {\displaystyle \psi } \sin \theta \cdot \cos \varphi ; \quad \left( {\displaystyle \dot {\displaystyle \psi }{\displaystyle \bf e}_{z_{0} } } \right)_{z} = \dot {\displaystyle \psi } \cos \theta ;$

(1.29)

$\left( {\displaystyle \dot {\displaystyle \theta }{\displaystyle \bf e}_{OA} } \right)_{x} = \dot {\displaystyle \theta }\cos \varphi ; \quad \left( {\displaystyle \dot {\displaystyle \theta }{\displaystyle \bf e}_{OA} } \right)_{y} = - \dot {\displaystyle \theta }\sin \varphi ; \quad \left( {\displaystyle \dot {\displaystyle \theta }{\displaystyle \bf e}_{OA} } \right)_{z} = 0.$

(1.30)

Iz (1.27 - 1.30) poluchim:

$\omega _{x} = \dot {\displaystyle \psi }\sin \theta \sin \varphi + \dot {\displaystyle \theta }\cos\varphi ;$

(1.31)

$\omega _{y} = \dot {\displaystyle \psi }\sin \theta \cos \varphi - \dot {\displaystyle \theta }\sin\varphi ;$

(1.32)

$\omega _{z} = \dot {\displaystyle \varphi } + \dot {\displaystyle \psi }\cos \theta .$

(1.33)

Uravneniya (1.31-1.33) nazyvayutsya kinematicheskimi uravneniyami Eilera. Oni, v chastnosti, pozvolyayut opredelit' velichinu i napravlenie vektora mgnovennoi uglovoi skorosti $\omega,$ esli zakon dvizheniya tela zadan v vide (1.22).

V ryade sluchaev vrashenie tela s zakreplennoi tochkoi vokrug mgnovennoi osi udobno predstavit' kak superpoziciyu dvuh vrashenii vokrug peresekayushihsya osei. V sluchae, izobrazhennom na ris. 1.22, vershina konusa sharnirno zakreplena v tochke O; os' konusa gorizontal'na, a osnovanie konusa katitsya bez proskal'zyvaniya po gorizontal'noi ploskosti S. Vektor uglovoi skorosti $\omega$ napravlen vdol' mgnovennoi osi vrasheniya OM (skorost' tochek O i M ravna nulyu); pri dvizhenii konusa mgnovennaya os' vrasheniya izmenyaet svoe polozhenie, opisyvaya nekotoruyu konicheskuyu poverhnost' s vershinoi v tochke O. Absolyutnoe vrashenie konusa s uglovoi skorost'yu $\omega$ mozhno predstavit' v vide summy

$\omega = \omega_{1} + \omega_{2} ,$

(1.34)

gde $\omega_{1}$ - uglovaya skorost' otnositel'nogo vrasheniya konusa vokrug sobstvennoi osi simmetrii, $\omega_{2}$ - uglovaya skorost' perenosnogo vrasheniya samoi osi konusa vokrug vertikali. Esli zadana $\omega _{2} ,$ to

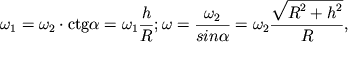$\omega _{1} = \omega _{2} \cdot {\displaystyle \rm ctg}\alpha = \omega _{1} {\displaystyle \frac{\displaystyle {\displaystyle h}}{\displaystyle {\displaystyle R}}}; \omega = {\displaystyle \frac{\displaystyle {\displaystyle \omega _{2} }}{\displaystyle {\displaystyle sin\alpha }}} = \omega _{2} {\displaystyle \frac{\displaystyle {\displaystyle \sqrt {\displaystyle R^{2} + h^{2}} }}{\displaystyle {\displaystyle R}}},$

gde $\alpha$ - ugol polurastvora konusa, $R$ - radius osnovaniya konusa, $h$ - ego vysota.

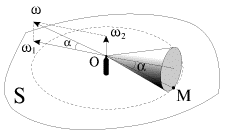Ris. 1.22.

Zamechanie. Dvizhenie tela, predstavlyayushee soboi odnovremennoe vrashenie vokrug neskol'kih osei s uglovymi skorostyami $\omega_{1} , \omega_{2} , \omega_{3} , \ldots$ mozhet byt' svedeno k vrasheniyu vokrug odnoi osi s uglovoi skorost'yu

$\omega = \omega_{1} + \omega_{2} + \omega_{3} + \ldots,$

(1.35)

Dvizhenie svobodnogo tverdogo tela.

Svobodnoe tverdoe telo mozhet sovershat' lyubye peremesheniya otnositel'no laboratornoi sistemy XYZ. V etom, samom obshem sluchae, ono imeet 6 stepenei svobody.

Opirayas' na teoremu Eilera (sm. vyshe), dvizhenie svobodnogo tverdogo tela mozhno predstavit' v vide superpozicii postupatel'nogo dvizheniya, pri kotorom vse tochki dvizhutsya kak proizvol'no vybrannyi polyus (nachalo sistemy x₀y₀z₀) i vrashatel'nogo dvizheniya vokrug mgnovennoi osi, prohodyashei cherez etot polyus. Etomu rassmotreniyu sootvetstvuyut 6 nezavisimyh koordinat: 3 dekartovy koordinaty X, Y, Z tochki, prinyatoi za polyus, i 3 ugla Eilera $\varphi , \psi , \theta$ (sm. ris. 1.3).

Polozhenie proizvol'noi tochki A tela v laboratornoi sisteme XYZ opredelyaetsya radius-vektorom $\bf r}_{A$ :

${\displaystyle \bf r}_{A} = {\displaystyle \bf r}_{O} + {\displaystyle \bf {\displaystyle r}'}_{A} ,$

(1.36)

gde $\bf r}_{O$ - radius-vektor tochki O, prinyatoi za polyus, ${\displaystyle \bf r}}'_{A$ - radius-vektor tochki A otnositel'no polyusa.

Skorost' tochki A

${\displaystyle \bf v}_{A} = {\displaystyle \bf v}_{O} + \omega\times {\displaystyle {\displaystyle \bf r}}'_{A} ,$

(1.37)

gde $\bf v}_{O$ - skorost' polyusa, a $\omega\times {\displaystyle {\displaystyle \bf r}}'_{A}$ - lineinaya skorost' vrashatel'nogo dvizheniya vokrug osi, prohodyashei cherez polyus. Uskorenie tochki A

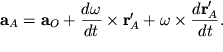${\displaystyle \bf a}_{A} = {\displaystyle \bf a}_{O} + {\displaystyle \frac{\displaystyle {\displaystyle d\omega}}{\displaystyle {\displaystyle dt}}}\times {\displaystyle {\displaystyle \bf r}}'_{A} + \omega\times {\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle {\displaystyle \bf r}}'_{A} }}{\displaystyle {\displaystyle dt}}}.$

(1.38)

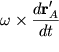Zdes' $\bf a}_{O$ - uskorenie polyusa, $\frac{\displaystyle {\displaystyle d\omega}}{\displaystyle {\displaystyle dt}}}\times {\displaystyle {\displaystyle \bf r}}'_{A$ - uskorenie, obuslovlennoe izmeneniem vektora mgnovennoi uglovoi skorosti $\omega$ po velichine i napravleniyu, $\omega\times {\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle {\displaystyle \bf r}}'_{A} }}{\displaystyle {\displaystyle dt}}}$ - centrostremitel'noe uskorenie (sm. formulu (1.26)).

Zamechanie 1. Prinimaya za polyus razlichnye tochki svobodnogo tverdogo tela (ili dazhe tochki vne ego), mozhno poluchit' beschislennoe mnozhestvo razlozhenii ego dvizheniya na postupatel'noe i vrashatel'noe Pri etom, kak i v sluchae ploskogo dvizheniya, kinematicheskie harakteristiki perenosnogo postupatel'nogo dvizheniya $\bf v}_{O}, {\displaystyle \bf a}_{O$ budut zaviset' ot vybora polyusa. Kinematicheskie zhe harakteristiki otnositel'nogo vrashatel'nogo dvizheniya $\omega, {\displaystyle \frac{\displaystyle {\displaystyle d\omega}}{\displaystyle {\displaystyle dt}}}$ ot vybora polyusa na zavisyat.

Zamechanie 2. Proizvol'noe (neploskoe) dvizhenie tverdogo tela nevozmozhno svesti k chistomu vrasheniyu vokrug mgnovennoi osi. Odnako mozhno pokazat', chto v etom sluchae sushestvuet mgnovennaya os' tak nazyvaemogo vintovogo peremesheniya tverdogo tela. Proizvol'noe dvizhenie tverdogo tela v XYZ v lyuboi moment vremeni mozhno predstavit' v vide superpozicii vrashatel'nogo dvizheniya vokrug nekotoroi osi i postupatel'nogo peremesheniya vdol' etoi zhe samoi osi. Estestvenno, s techeniem vremeni polozhenie mgnovennoi osi vintovogo peremesheniya v prostranstve i otnositel'no tela v obshem sluchae izmenyaetsya.

Nazad| Vpered

Publikacii s klyuchevymi slovami: mehanika - tverdoe telo - ugly Eilera Publikacii so slovami: mehanika - tverdoe telo - ugly Eilera
Sm. takzhe: Mehanika sploshnyh sred Variacionnye principy mehaniki Anizotropiya

Mneniya chitatelei [2]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce