Astronet > Mehanika tverdogo tela. Lekcii.

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Mehanika tverdogo tela. Lekcii.

V.A.Aleshkevich, L.G.Dedenko, V.A.Karavaev (Fizicheskii fakul'tet MGU)
Izdatel'stvo Fizicheskogo fakul'teta MGU, 1997 g. Soderzhanie

Lekciya 2.

Dinamika absolyutno tverdogo tela Moment impul'sa. Tenzor inercii. Moment impul'sa tela otnositel'no osi. Ellipsoid inercii. Vychislenie momentov inercii otnositel'no osi. Teorema Gyuigensa-Shteinera. Moment impul'sa otnositel'no dvizhushegosya centra mass.

Zadacha dinamiki absolyutno tverdogo tela - izuchit' dvizhenie tela v zavisimosti ot deistvuyushih na nego sil. Kak sleduet iz predydushego rassmotreniya, proizvol'noe dvizhenie tverdogo tela mozhno svesti k postupatel'nomu i vrashatel'nomu. Pri postupatel'nom dvizhenii traektorii vseh tochek tela odinakovy, i dlya opisaniya etogo dvizheniya ispol'zuyutsya takie ponyatiya, kak massa, impul's, sila. Pri izuchenii vrashatel'nogo dvizheniya tela etih ponyatii okazyvaetsya nedostatochno.

Rassmotrim dva cilindra odinakovoi massy i odinakovyh razmerov, prichem odin cilindr, izgotovlennyi iz bolei legkogo materiala, pust' budet sploshnym, a drugoi, izgotovlennyi iz bolee tyazhelogo materiala, - polym. Opyt pokazyvaet, chto pri soskal'zyvanii s dostatochno gladkoi naklonnoi ploskosti cilindry ne vrashayutsya i vedut sebya sovershenno odinakovo (ris. 2.1a) v chastnosti, oni odnovremenno dostigayut osnovaniya etoi naklonnoi ploskosti. Inoe delo, esli ploskost' sherohovataya, i cilindry skatyvayutsya, vrashayas' vokrug svoei osi (ris. 2.1b) - v etom sluchae bystree skatyvaetsya sploshnoi cilindr. Takim obrazom, pri vrashatel'nom dvizhenii sushestvenno raspredelenie massy otnositel'no osi vrasheniya.

Ris. 2.1.

Ob etom zhe svidetel'stvuyut i drugie opyty: chem dal'she ot osi vrasheniya sosredotochena massa tela, tem trudnee ego raskrutit' pri vozdeistvii postoyannoi siloi, imeyushei odno i to zhe plecho (ris. 2.2ab). Dlya raskruchivaniya sterzhnei s gruzami do uglovoi skorosti $\omega _{0}$ v sluchae ris. 2.2b trebuetsya bol'shee vremya, chem v sluchae ris. 2.2a. V etih zhe opytah mozhno pokazat', chto pri vrashatel'nom dvizhenii tela sushestvennuyu rol' igraet ne sama sila, a ee moment: esli perebrosit' nit' na shkiv bol'shego radiusa, to raskrutit' eti tela budet legche (ris. 2.2v). Takim obrazom, dlya opisaniya vrashatel'nogo dvizheniya tela neobhodimo vvesti novye ponyatiya: moment inercii, moment impul'sa, moment sily.

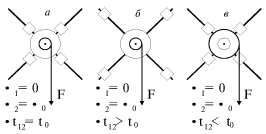Ris. 2.2.

Moment impul'sa. Tenzor inercii.

Moment impul'sa tela otnositel'no nepodvizhnoi tochki - vazhneishee ponyatie v dinamike vrashatel'nogo dvizheniya tverdogo tela. On opredelyaetsya tak zhe, kak i dlya sistemy material'nyh tochek:

${\displaystyle \bf L} = {\displaystyle \sum\limits_{i} {\displaystyle {\displaystyle \bf r}_{i}} }\times {\displaystyle \bf p}_{i} = {\displaystyle \sum\limits_{i} {\displaystyle \Delta m_{i} } }{\displaystyle \bf r}_{i} \times v_{i} .$

(2.1)

Zdes' $\Delta {\displaystyle \bf p}_{i} = \Delta m_{i} {\displaystyle \bf v}_{i}$ - impul's elementarnoi $\Delta m_{i}$ v laboratornoi sisteme XYZ, a $\bf r}_{i$ - radius-vektor massy $\Delta m_{i}$ s nachalom v toi nepodvizhnoi tochke, otnositel'no kotoroi vychislyaetsya moment impul'sa tela.

S uchetom postoyanstva rasstoyanii mezhdu tochkami absolyutno tverdogo tela vektor momenta impul'sa L udaetsya svyazat' s vektorom uglovoi skorosti $\omega.$

Rassmotrim, k primeru, dve odinakovye tochechnye massy $m,$ ukreplennye na koncah nevesomogo sterzhnya AV (ris. 2.V). Sterzhen' s massami vrashaetsya s uglovoi skorost'yu $\omega$ vokrug vertikal'noi osi, prohodyashei cherez seredinu sterzhnya i perpendikulyarnoi emu. V etom sluchae

${\displaystyle \bf L} = m{\displaystyle \bf r}_{1} \times {\displaystyle \bf v}_{1} + m{\displaystyle \bf r}_{2}\times {\displaystyle \bf v}_{2} = 2mr^{2}\omega$

(2.2)

Zdes' uchteno, chto $r_{1} = r_{2} = r,$ a $v_{1} = v_{2} = \omega r.$

Ris. 2.3.

Sushestvenno, chto v etom primere vektor L, napravlen tak zhe, kak i $\omega.$ K sozhaleniyu, tak byvaet ne vsegda. V etom mozhno ubedit'sya na primere, pokazannom na ris. 2.4. Zdes' nevesomyi sterzhen' AV s dvumya massami $m$ na koncah zhestko zakreplen na vertikal'noi osi (v tochke O) pod nekotorym uglom $\alpha$ k nei i lezhit v ploskosti Oyz. Pri vrashenii sterzhnya vokrug vertikal'noi osi s uglovoi skorost'yu $\omega$ vektor L, opredelennyi po (2.1), budet nahodit'sya v ploskosti Oyz i sostavit ugol ${\displaystyle \frac{\displaystyle {\displaystyle \pi }}{\displaystyle {\displaystyle 2}}} - \alpha$ s os'yu z. Sistema xyz, vvedennaya v nachale lekcii 1, zhestko svyazana so sterzhnem i povorachivaetsya vmeste s nim. Pri etom vektor L ostaetsya v ploskosti Oyz, a v laboratornoi sisteme dvizhetsya po konicheskoi poverhnosti s uglom polurastvora ${\displaystyle \frac{\displaystyle {\displaystyle \pi }}{\displaystyle {\displaystyle 2}}} - \alpha$

Ris. 2.4.

Poluchim vyrazhenie dlya L v sluchae tverdogo tela proizvol'noi formy, zakreplennogo v nekotoroi tochke O.

Pust' $\bf r}_{i$ - radius-vektor elementarnoi massy $\Delta m_{i}$ tverdogo tela, a $\omega$ - uglovaya skorost'. Togda

$\bf L} = {\displaystyle \sum\limits_{i} {\displaystyle \Delta m_{i} } }{\displaystyle \bf r}_{i} \times {\displaystyle \bf v}_{i} = {\displaystyle \sum\limits_{i} {\displaystyle \Delta m_{i} } }{\displaystyle \mathop {\displaystyle {\displaystyle \bf r}_{i} }\limits_{a} }\times {\displaystyle \mathop {\displaystyle (\omega}\limits_{b} }\times {\displaystyle \mathop {\displaystyle {\displaystyle \bf r}_{i} )}\limits_{c} } = {\displaystyle \sum\limits_{i} {\displaystyle \Delta m_{i} } }{\displaystyle \left\{\displaystyle {\displaystyle {\displaystyle \mathop {\displaystyle \omega}\limits_{b} }({\displaystyle \mathop {\displaystyle {\displaystyle \bf r}_{i} }\limits_{a} }{\displaystyle \mathop {\displaystyle {\displaystyle \bf r}_{i} }\limits_{c} }) - {\displaystyle \mathop {\displaystyle {\displaystyle \bf r}_{i} }\limits_{c} }({\displaystyle \mathop {\displaystyle {\displaystyle \bf r}_{i} }\limits_{a} }{\displaystyle \mathop {\displaystyle \omega}\limits_{b} })} \right\}} = {\displaystyle \sum\limits_{i} {\displaystyle \Delta m_{i} } }{\displaystyle \left\{\displaystyle {\displaystyle \omega r_{i}^{2} - r_{i} (r_{i} \omega)} \right\}$

(2.3)

Vektory $r_{i} , \omega$ i L mozhno proektirovat' kak na osi laboratornoi sistemy XYZ, tak i na osi sistemy xyz, zhestko svyazannoi s tverdym telom (poskol'ku tochka O nepodvizhna, nachala obeih sistem mozhno sovmestit'). Preimushestvo sistemy xyz zaklyuchaetsya v tom, chto v nei proekcii $\bf r}_{i$ yavlyayutsya postoyannymi velichinami (v sisteme XYZ oni zavisyat ot vremeni), i vyrazheniya dlya komponent L, okazyvayutsya proshe.

Itak, v sisteme xyz

${\displaystyle \bf r}_{i} = {\displaystyle \left\{\displaystyle {\displaystyle x_{i} ,y_{i} ,z_{i} } \right\}}, \quad \omega = {\displaystyle \left\{\displaystyle {\displaystyle \omega _{x} ,\omega _{y} ,\omega _{z} } \right\}}.$

(2.4)

Togda, prodolzhaya (2.3), mozhno zapisat':

$\bf L} = {\displaystyle \sum\limits_{i} {\displaystyle \Delta m_{i} } }{\displaystyle \left\{\displaystyle {\displaystyle \omega r_{i}^{2} - r_{i} (x_{i} \omega _{x} + y_{i} \omega _{y} + z_{i} \omega _{z} )} \right\}$

(2.5)

Vyrazheniya dlya proekcii momenta impul'sa na osi sistemy xyz zapishem v sleduyushem vide:

$L_{x} = {\displaystyle \sum\limits_{i} {\displaystyle \Delta m_{i} \left( {\displaystyle r_{i}^{2} - x_{i}^{2} } \right)} }\omega _{x} + {\displaystyle \sum\limits_{i} {\displaystyle \left( {\displaystyle - \Delta m_{i} x_{i} y_{i} } \right)} }\omega _{y} + {\displaystyle \sum\limits_{i} {\displaystyle \left( {\displaystyle - \Delta m_{i} x_{i} z{\displaystyle }_{i}} \right)} }\omega _{z} ;$

(2.6)

$L_{y} = {\displaystyle \sum\limits_{i} {\displaystyle \left( {\displaystyle - \Delta m_{i} y_{i} x_{i} } \right)} }\omega _{x} + {\displaystyle \sum\limits_{i} {\displaystyle \Delta m_{i} \left( {\displaystyle r_{i}^{2} - y_{i}^{2} } \right)} }\omega _{y} + {\displaystyle \sum\limits_{i} {\displaystyle \left( {\displaystyle - \Delta m_{i} y_{i} z{\displaystyle }_{i}} \right)} }\omega _{z} ;$

(2.7)

$L_{z} = {\displaystyle \sum\limits_{i} {\displaystyle \left( {\displaystyle - \Delta m_{i} z_{i} x_{i} } \right)} }\omega _{x} + {\displaystyle \sum\limits_{i} {\displaystyle \left( {\displaystyle - \Delta m_{i} z_{i} y{\displaystyle }_{i}} \right)} }\omega _{y} + {\displaystyle \sum\limits_{i} {\displaystyle \Delta m_{i} \left( {\displaystyle r_{i}^{2} - z_{i}^{2} } \right)} }\omega _{z} ,$

(2.8)

ili

$L_{x} = J_{xx} \omega _{x} + J_{xy} \omega _{y} + J_{xz} \omega _{z} ;$

(2.9)

$L_{y} = J_{yx} \omega _{x} + J_{yy} \omega _{y} + J_{xy} \omega _{z} ;$

(2.10)

$L_{z} = J_{zx} \omega _{x} + J_{zy} \omega _{y} + J_{zz} \omega _{z} ;$

(2.11)

gde $J_{kl}$ - 9 komponent tak nazyvaemogo tenzora inercii $\hat {\displaystyle J}$ tverdogo tela otnositel'no tochki O:

$\hat {\displaystyle J} = \left( {\displaystyle {\displaystyle \begin{array}{*{20}c} {\displaystyle J_{xx} } \hfill & {\displaystyle J_{xy} } \hfill & {\displaystyle J_{xz} } \hfill \\ {\displaystyle J_{yx} } \hfill & {\displaystyle J_{yy} } \hfill & {\displaystyle J_{yz} } \hfill \\ {\displaystyle J_{zx} } \hfill & {\displaystyle J_{zy} } \hfill & {\displaystyle J_{zz} } \hfill \\ \end{array} }} \right)$

(2.)

Diagonal'nye elementy tenzora $J_{xx} , J_{yy} , J_{zz}$ nazyvayutsya osevymi momentami inercii, nediagonal'nye elementy $J_{xy} , J_{yx} , J_{xz} , J_{zx} , J_{yz} , J_{zy}$ nazyvayutsya centrobezhnymi momentami inercii. Obratim vnimanie, chto $J_{xy} = J_{yx} , J_{xz} = J_{zx} , J_{yz} = J_{zy} .$ Takoi tenzor nazyvayut simmetrichnym.

Esli koordinatam x, y i z prisvoit' nomera 1, 2 i 3 sootvetstvenno, to (2.9-2.11) mozhno predstavit' v vide

$L_{k} = {\displaystyle \sum\limits_{\ell = 1}^{3} {\displaystyle J_{kl} } }\omega _{l} ;\quad k, \ell = 1, 2, 3.$

(2.13)

V simvolicheskom vide mozhno zapisat' tak:

$L = \hat {\displaystyle J}\omega$

(2.14)

Samoe glavnoe, chto stoit za privedennymi vyshe formulami, zaklyuchaetsya v sleduyushem. Devyat' velichin $J_{k\ell }$ (iz nih shest' nezavisimyh) opredelyayut odnoznachnuyu svyaz' mezhdu L i $\omega,$ prichem okazyvaetsya, chto L, voobshe govorya, ne sovpadaet po napravleniyu s $\omega$ (ris. 2.5)

Ris. 2.5.

Itak, my stolknulis' s novym tipom velichin, imeyushim vazhnoe znachenie v fizike - tenzorom. Esli dlya zadaniya skalyarnoi velichiny neobhodimo odno chislo (znachenie skalyarnoi velichiny), vektornoi - tri chisla (tri proekcii vektora na osi dekartovoi sistemy koordinat), to dlya zadaniya tenzora neobhodimy v obshem sluchae 9 chisel. Na yazyke matematiki tenzor - eto mnogokomponentnaya velichina, harakterizuyushayasya opredelennym povedeniem pri preobrazovaniyah sistemy koordinat (v dannom sluchae komponenty tenzora inercii preobrazuyutsya kak proizvedeniya sootvetstvuyushih koordinat).

Nazad| Vpered

Publikacii s klyuchevymi slovami: mehanika - tverdoe telo - ugly Eilera Publikacii so slovami: mehanika - tverdoe telo - ugly Eilera
Sm. takzhe: Mehanika sploshnyh sred Variacionnye principy mehaniki Anizotropiya

Mneniya chitatelei [2]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce