Astronet > Mehanika tverdogo tela. Lekcii.

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Mehanika tverdogo tela. Lekcii.

V.A.Aleshkevich, L.G.Dedenko, V.A.Karavaev (Fizicheskii fakul'tet MGU)
Izdatel'stvo Fizicheskogo fakul'teta MGU, 1997 g. Soderzhanie

Neobhodimost' vvedeniya tenzornyh velichin svyazana s razlichnogo roda anizotropiei svoistv fizicheskih makroskopicheskih ob'ektov. Tenzor svyazyvaet dve vektornye velichiny, kotorye proporcional'ny drug drugu po modulyu, no v silu anizotropii svoistv ob'ekta ne sovpadayut drug s drugom po napravleniyu. V sluchae L i $\omega$ reshayushuyu rol' igraet "anizotropiya" formy tela (otsutstvie opredelennoi simmetrii otnositel'no osei xyz). V drugih sluchayah eto mozhet byt' anizotropiya, naprimer, elektricheskih ili magnitnyh svoistv veshestva. Tak, vektory polyarizacii veshestva R i napryazhennosti elektricheskogo polya E svyazany tenzorom polyarizuemosti $\hat {\displaystyle \alpha }$ : $\bf P} = \varepsilon _{0} \hat {\displaystyle \alpha }{\displaystyle \bf E} (\varepsilon _{0$ - elektricheskaya postoyannaya). Eto oznachaet, chto v silu anizotropii elektricheskih svoistv veshestvo polyarizuetsya "ne po polyu", to est' "ne po polyu" smeshayutsya polozhitel'nye i otricatel'nye zaryady v molekulah veshestva. Primerami drugih, v obshem sluchae tenzornyh velichin yavlyayutsya dielektricheskaya pronicaemost' i magnitnaya pronicaemost' veshestva. Vazhnuyu rol' v mehanike igrayut tenzory deformacii i napryazhenii. S etimi i drugimi tenzornymi velichinami vy poznakomites' pri izuchenii sootvetstvuyushih razdelov kursa obshei fiziki.

Zamechanie. Esli ${\displaystyle \bf r}_{i} , \omega$ i L v vyrazhenii (2.3) proektirovat' na osi laboratornoi sistemy XYZ, to komponenty tenzora $J_{k\ell }$ okazalis' by zavisyashimi ot vremeni. Takoi podhod v principe vozmozhen; on, v chastnosti, ispol'zuetsya v Berkleevskom kurse fiziki [Ch. Kittel' i dr., 1983].

Glavnye osi inercii.

Voznikaet vopros: vozmozhen li dlya proizvol'nogo tverdogo tela sluchai, kogda vektory L i $\omega$ sovpadayut? Okazyvaetsya, chto dlya vsyakogo tela i lyuboi tochki O imeyutsya po krainei mere tri vzaimno perpendikulyarnyh napravleniya $\omega$ (ili, drugimi slovami, tri vzaimno perpendikulyarnyh osi vrasheniya), dlya kotoryh napravleniya L i $\omega$ sovpadayut. Takie osi nazyvayutsya glavnymi osyami inercii tela.

Esli osi Ox, Oy i Oz sovmestit' s glavnymi osyami inercii tela, to matrica $J_{k\ell }$ budet imet' diagonal'nyi vid:

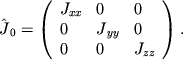$\hat {\displaystyle J}_{0} = \left( {\displaystyle {\displaystyle \begin{array}{*{20}c} {\displaystyle J_{xx} } \hfill & {\displaystyle 0} \hfill & {\displaystyle 0} \hfill \\ {\displaystyle 0} \hfill & {\displaystyle J{\displaystyle }_{yy}} \hfill & {\displaystyle 0} \hfill \\ {\displaystyle 0} \hfill & {\displaystyle 0} \hfill & {\displaystyle J_{zz} } \hfill \\ \end{array} }} \right).$

(2.15)

Velichiny $J_{xx} \equiv J_{x} , J_{yy} \equiv J_{y} , J_{zz} \equiv J_{z}$ v etom sluchae nazyvayutsya glavnymi momentami inercii tela. Pri etom

$L_{x} = J_{x} \omega _{x} ; L_{y} = J_{y} \omega _{y} ; L_{z} = J_{z} \omega _{z} ,$

(2.16)

to est', deistvitel'no, esli vektor $\omega$ napravlen vdol' odnoi iz glavnyh osei inercii tela, to vektor L budet napravlen tochno tak zhe (ris. 2.6).

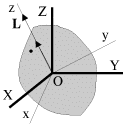Ris. 2.6.

Raspolozhenie glavnyh osei inercii v tele i znacheniya sootvetstvuyushih glavnyh momentov inercii zavisyat ot vybora tochki O. Esli O sovpadaet s centrom mass, to glavnye osi nazyvayutsya glavnymi central'nymi osyami tela. Esli glavnye osi inercii tela izvestny, to znacheniya glavnyh momentov inercii vychislyayutsya iz geometrii mass. Naprimer:

$J_{x} = {\displaystyle \sum\limits_{i} {\displaystyle \Delta m_{i} } }\left( {\displaystyle r_{i}^{2} - x_{i}^{2} } \right) = {\displaystyle \sum\limits_{i} {\displaystyle \Delta m_{i} } }\left( {\displaystyle y_{i}^{2} + z_{i}^{2} } \right) = {\displaystyle \sum\limits_{i} {\displaystyle \Delta m_{i} } }\rho _{i}^{2} .$

(2.17)

Zdes' $\rho _{i}$ - rasstoyanie elementarnoi massy $\Delta m_{i}$ ot glavnoi osi Ox.

Kak zhe opredelit' glavnye osi inercii dlya vybrannoi tochki O tverdogo tela? Esli osi Ox, Oy i Oz provedeny v tele proizvol'no, to v obshem sluchae oni ne sovpadayut s glavnymi osyami inercii. Takogo sovpadeniya mozhno dobit'sya putem nekotorogo povorota ishodnoi sistemy koordinat otnositel'no tverdogo tela. V novyh koordinatah matrica $J_{k\ell }$ stanovitsya diagonal'noi.

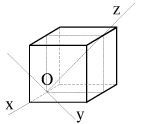
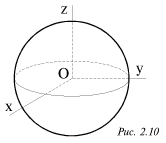
Vo mnogih sluchayah glavnye osi inercii udaetsya legko opredelit' iz soobrazhenii simmetrii. Na ris. 2.7-2.10 izobrazheny glavnye osi inercii dlya razlichnyh tochek tel, obladayushih opredelennoi simmetriei: cilindra (ris. 2.7), pryamougol'nogo parallelepipeda (ris. 2.8), kuba (ris. 2.9) i shara (ris. 2.10). Legko soobrazit', chto vo vseh etih sluchayah $J_{xy} = J_{xz} = J_{yx} = J_{yz} = J_{zx} = J_{zy} = 0.$ Naprimer, v sluchae pryamougol'nogo parallelepipeda (ris. 2.8) $J_{xy} = - {\displaystyle \sum\limits_{i} {\displaystyle \Delta m_{i} } }x_{i} y_{i} = 0,$ tak kak dlya vsyakoi massy $\Delta m_{i}$ s dannymi znacheniyami $x_{i} , y_{i} , z_{i}$ naidetsya simmetrichno raspolozhennaya massa $\Delta {\displaystyle m}'_{i}$ s temi zhe znacheniyami $x_{i}$ i $z_{i}$ , no s protivopolozhnym znacheniem $y_{i}.$


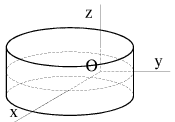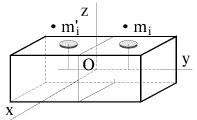Ris. 2.7.	Ris. 2.8.

Ris. 2.9.	Ris. 2.10.

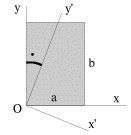
V zaklyuchenie etogo razdela rassmotrim primer nahozhdeniya glavnyh osei inercii dlya ploskoi pryamougol'noi plastinki so storonami $a$ i $b,$ massa kotoroi $m$ (ris. 2.11).

Ris. 2.11.

Yasno, chto odna iz glavnyh osei inercii dlya tochki O (os' Oz) perpendikulyarna ploskosti plastinki; na ris. 2.11 ona ne pokazana. Osi Ox i Oy, napravlennye vdol' storon plastinki, ne yavlyayutsya glavnymi. Deistvitel'no, v etom sluchae

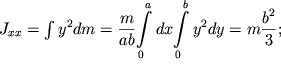$J_{xx} = \int {\displaystyle y^{2}} dm = {\displaystyle \frac{\displaystyle {\displaystyle m}}{\displaystyle {\displaystyle ab}}}{\displaystyle \int\limits_{0}^{a} {\displaystyle dx{\displaystyle \int\limits_{0}^{b} {\displaystyle y^{2}} }} }dy = m{\displaystyle \frac{\displaystyle {\displaystyle b^{2}}}{\displaystyle {\displaystyle 3}}};$

(2.18)

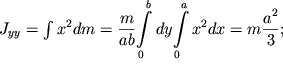$J_{yy} = \int {\displaystyle x^{2}} dm = {\displaystyle \frac{\displaystyle {\displaystyle m}}{\displaystyle {\displaystyle ab}}}{\displaystyle \int\limits_{0}^{b} {\displaystyle dy{\displaystyle \int\limits_{0}^{a} {\displaystyle x^{2}} }} }dx = m{\displaystyle \frac{\displaystyle {\displaystyle a^{2}}}{\displaystyle {\displaystyle 3}}};$

(2.19)

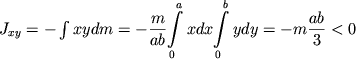$J_{xy} = - \int {\displaystyle xy} dm = - {\displaystyle \frac{\displaystyle {\displaystyle m}}{\displaystyle {\displaystyle ab}}}{\displaystyle \int\limits_{0}^{a} {\displaystyle xdx{\displaystyle \int\limits_{0}^{b} {\displaystyle y} }} }dy = - m{\displaystyle \frac{\displaystyle {\displaystyle ab}}{\displaystyle {\displaystyle 3}}} \lt 0$

(2.20)

Dopustim, chto osi Ox' i Oy', povernutye na ugol $\alpha$ otnositel'no osei Ox i Oy - glavnye osi inercii dlya tochki O. Sootvetstvuyushee preobrazovanie koordinat imeet vid:

$\left\{\displaystyle {\displaystyle \begin{array}{l} {\displaystyle x = {\displaystyle x}'\cos \alpha + {\displaystyle y}'\sin \alpha ;} \\ {\displaystyle y = - {\displaystyle x}'\sin \alpha + {\displaystyle y}'\cos \alpha } \\ \end{array}} \right.}. \quad \begin{array}{l} (1.21) \\ (1.22) \\ \end{array$

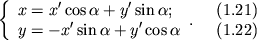Togda budem imet'

$J_{xx} = \int {\displaystyle y^{2}} dm = \int {\displaystyle \left( {\displaystyle - {\displaystyle x}'\sin \alpha + {\displaystyle y}'\cos \alpha } \right)} ^{2}dm = J_{{\displaystyle y}'} \sin ^{2}\alpha + J_{{\displaystyle x}'} \cos ^{2}\alpha .$

(2.23)

Zdes' uchteno, chto dlya glavnyh osei Ox' i Oy' $\int {\displaystyle {\displaystyle x}'{\displaystyle y}'dm = 0.}$

Analogichno

$J_{yy} = \int {\displaystyle x^{2}} dm = \int {\displaystyle \left( {\displaystyle {\displaystyle x}'\cos \alpha + {\displaystyle y}'\sin \alpha } \right)} ^{2}dm = J_{{\displaystyle y}'} \cos ^{2}\alpha + J_{{\displaystyle x}'} \sin ^{2}\alpha .$

(2.24)

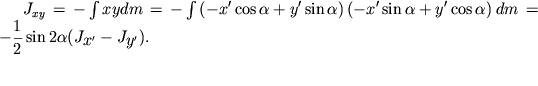$J_{xy} = - \int {\displaystyle xy} dm = - \int {\displaystyle \left( {\displaystyle - {\displaystyle x}'\cos \alpha + {\displaystyle y}'\sin \alpha } \right)\left( {\displaystyle - {\displaystyle x}'\sin \alpha + {\displaystyle y}'\cos \alpha } \right){\displaystyle \kern 1pt} } dm = - {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}\sin 2\alpha (J_{{\displaystyle x}'} - J_{{\displaystyle y}'} ).$

(2.25)

Podstavlyaya v (2.23 - 2.25) znacheniya $J_{xx} , J_{yy}$ i $J_{xy}$ iz (2.18 - 2.20), poluchim sistemu treh uravnenii dlya nahozhdeniya $J_{{\displaystyle x}'} , J_{{\displaystyle y}'}$ i $\alpha$ :

$\left\{\displaystyle {\displaystyle \begin{array}{l} {\displaystyle J_{{\displaystyle y}'} \sin ^{2}\alpha + J_{{\displaystyle x}'} \cos ^{2}\alpha = m{\displaystyle \frac{\displaystyle {\displaystyle b^{2}}}{\displaystyle {\displaystyle 3}}};} \\ {\displaystyle J_{{\displaystyle y}'} \cos ^{2}\alpha + J_{{\displaystyle x}'} \sin ^{2}\alpha = m{\displaystyle \frac{\displaystyle {\displaystyle a^{2}}}{\displaystyle {\displaystyle 3}}};} \\ {\displaystyle \left( {\displaystyle J_{{\displaystyle x}'} - J_{{\displaystyle y}'} } \right)\sin 2\alpha = m{\displaystyle \frac{\displaystyle {\displaystyle ab}}{\displaystyle {\displaystyle 3}}};} \\ \end{array}} \right.} \quad \begin{array}{l} (2.26) \\ (2.27) \\ (2.28) \\ \end{array$

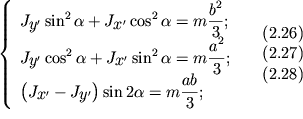Iz etoi sistemy, v chastnosti, legko poluchit', chto

${\displaystyle \rm tg}2\alpha = {\displaystyle \frac{\displaystyle {\displaystyle 3}}{\displaystyle {\displaystyle 2}}} \cdot {\displaystyle \frac{\displaystyle {\displaystyle ab}}{\displaystyle {\displaystyle \left( {\displaystyle b^{2} - a^{2}} \right)}}}.$

(2.29)

Dlya sravneniya: esli $\alpha _{0}$ - ugol mezhdu os'yu Oy i diagonal'yu pryamougol'noi plastinki, to

${\displaystyle \rm tg}2\alpha _{0} = {\displaystyle \frac{\displaystyle {\displaystyle 2ab}}{\displaystyle {\displaystyle b^{2} - a^{2}}}},$

(2.30)

to est' $\alpha \lt \alpha _{0} .$ Eto oznachaet, chto glavnaya os' inercii Oy' ne prohodit cherez centr plastinki. I tol'ko v sluchae kvadrata, kogda $a = b, \alpha = {\displaystyle \frac{\displaystyle {\displaystyle \pi }}{\displaystyle {\displaystyle 4}}},$ glavnaya os' inercii Oy' budet napravlena po diagonali kvadrata. Etot primer naglyadno pokazyvaet, chto esli glavnye osi inercii - necentral'nye, to ni odna iz nih v principe mozhet i ne prohodit' cherez centr mass tela.

Nazad| Vpered

Publikacii s klyuchevymi slovami: mehanika - tverdoe telo - ugly Eilera Publikacii so slovami: mehanika - tverdoe telo - ugly Eilera
Sm. takzhe: Mehanika sploshnyh sred Variacionnye principy mehaniki Anizotropiya

Mneniya chitatelei [2]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce