Astronet > Mehanika tverdogo tela. Lekcii.

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Mehanika tverdogo tela. Lekcii.

V.A.Aleshkevich, L.G.Dedenko, V.A.Karavaev (Fizicheskii fakul'tet MGU)
Izdatel'stvo Fizicheskogo fakul'teta MGU, 1997 g. Soderzhanie

Moment impul'sa tverdogo tela otnositel'no osi. Moment inercii otnositel'no osi.

V teh sluchayah, kogda tverdoe telo vrashaetsya vokrug nepodvizhnoi osi, obychno operiruyut s ponyatiyami momenta impul'sa i momenta inercii otnositel'no osi. Moment impul'sa $L_{\parallel}$ otnositel'no osi - eto proekciya na dannuyu os' momenta impul'sa L, opredelennogo otnositel'no nekotoroi tochki O, prinadlezhashei osi, prichem, kak okazyvaetsya, vybor tochki O na osi znacheniya ne imeet.

Deistvitel'no, pri vychislenii $L_{\parallel}$ sushestvenno lish' plecho impul'sa $\Delta {\displaystyle \bf p}_{i} = \Delta m_{i} {\displaystyle \bf v}_{i}$ otnositel'no osi vrasheniya O'O'' (ris. 2.12), to est' kratchaishee rasstoyanie $\rho _{i}$ massy $\Delta m_{i}$ do osi:

$\left( {\displaystyle L_{i} } \right)_{\parallel} = \Delta m_{i} (r_{i} ^{2}v_{i} )_{{\displaystyle \parallel}} = \Delta m_{i} \rho _{i} v_{i} = (\Delta m_{i} \rho _{i}^{2} )\omega$

(2.31)

Zdes' uchteno, chto skorost' massy $\Delta m_{i}$ pri vrashatel'nom dvizhenii $v_{i} = \omega \rho_{i} ; v_{i} \bot \rho_{i} .$

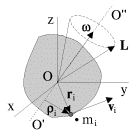Ris. 2.12.

Rassmotrim etu situaciyu bolee podrobno. Pust' osi Ox, Oy, Oz na ris. 2.12 - glavnye osi inercii dlya tochki O, O'O'' - nepodvizhnaya v laboratornoi sisteme os' vrasheniya, zhestko svyazannaya s telom. Vektor uglovoi skorosti $\omega,$ napravlennyi vdol' O'O'', mozhno razlozhit' po osyam sistemy koordinat xyz:

$\omega = {\displaystyle \left\{\displaystyle {\displaystyle \omega _{x} , \omega _{y} , \omega _{z} } \right\}} = {\displaystyle \left\{\displaystyle {\displaystyle \omega \cos \alpha , \omega cos\beta , \omega cos\gamma } \right\}},$

(2.32)

gde $\cos \alpha , cos\beta , cos\gamma$ - napravlyayushie kosinusy osi O'O''. Vektor L ne sovpadaet s $\omega$ i pri vrashenii tela opisyvaet konicheskuyu poverhnost', simmetrichnuyu otnositel'no O'O''.Vektor L takzhe mozhno razlozhit' po osyam sistemy xyz: ${\displaystyle \bf L} = {\displaystyle \left\{\displaystyle {\displaystyle L_{x} , L_{y} , L_{z} } \right\}},$ prichem

$L_{x} = J_{x} \omega _{x} ; L_{y} = J_{y} \omega _{y} ; L_{z} = J_{z} \omega _{z} ,$

(2.33)

gde $J_{x} , J_{y} , J_{z}$ - glavnye momenty inercii.

Proekciya vektora L na os' vrasheniya, ili, chto to zhe samoe, moment impul'sa otnositel'no osi

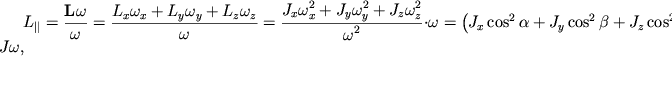$L_{\parallel} = {\displaystyle \frac{\displaystyle {\displaystyle {\displaystyle \bf L}\omega}}{\displaystyle {\displaystyle \omega }}} = {\displaystyle \frac{\displaystyle {\displaystyle L_{x} \omega _{x} + L_{y} \omega _{y} + L_{z} \omega _{z} }}{\displaystyle {\displaystyle \omega }}} = {\displaystyle \frac{\displaystyle {\displaystyle J_{x} \omega _{x}^{2} + J_{y} \omega _{y}^{2} + J_{z} \omega _{z}^{2} }}{\displaystyle {\displaystyle \omega ^{2}}}} \cdot \omega = \left( {\displaystyle J_{x} \cos ^{2}\alpha + J_{y} \cos ^{2}\beta + J_{z} \cos ^{2}\gamma } \right)\omega = J\omega ,$

(2.34)

gde

$J = J_{x} \cos ^{2}\alpha + J_{y} \cos ^{2}\beta + J_{z} \cos ^{2}\gamma$

(2.35)

- moment inercii otnositel'no osi.

Poslednyaya formula pozvolyaet rasschitat' moment inercii tverdogo tela otnositel'no proizvol'noi osi v tom sluchae, esli izvestny glavnye momenty inercii $J_{x} , J_{y} , J_{z}$ i orientaciya osi vrasheniya otnositel'no glavnyh osei inercii (ugly $\alpha , \beta , \gamma$ ). Vo mnogih sluchayah takoe vychislenie okazyvaetsya znachitel'no proshe, chem pryamoe raschet po formule

$J = {\displaystyle \sum\limits_{i} {\displaystyle \Delta m_{i} } }\rho _{i}^{2}$

(2.35)

(sm. (2.31)).

Otmetim, chto, v sootvetstvii s dannym vyshe opredeleniem, $L_{\parallel}$ - velichina skalyarnaya (proekciya vektora L na os' vrasheniya). Vmeste s tem mozhno govorit' i o vektore ${\displaystyle \bf L}_{\parallel} ,$ rassmatrivaya ego kak sostavlyayushuyu vektora L, vdol' osi:

$L_{\parallel} = {\displaystyle \sum\limits_{i} {\displaystyle \rho_{i} } }\times\Delta p_{i}$

(2.37)

(vektor $\rho_{i}$ izobrazhen na ris. 2.12, $\Delta p_{i} = \Delta m_{i} v_{i}$ ). V rekomenduemyh uchebnyh posobiyah mozhno vstretit' obe traktovki ponyatiya momenta impul'sa otnositel'no osi.

Ellipsoid inercii.

Formula (2.35) dlya momenta inercii otnositel'no osi dopuskaet naglyadnuyu geometricheskuyu interpretaciyu.

Predstavim, chto cherez tochku O nachala koordinat sistemy xyz my provodim pryamye vo vsevozmozhnyh napravleniyah i na nih otkladyvaem otrezki dlinoi $R = {\displaystyle \frac{\displaystyle {\displaystyle k}}{\displaystyle {\displaystyle \sqrt {\displaystyle J} }}}$ (ris. 2.13), gde $k$ est' postoyannaya velichina, imeyushaya razmernost' kg^1/2*m². Geometricheskim mestom koncov etih otrezkov budet nekotoraya poverhnost'. Poluchim uravnenie etoi poverhnosti.

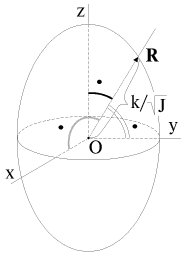Ris. 2.13.

Pust' osi Ox, Oy, Oz na ris. 2.13 - glavnye osi inercii. Proekcii vektora R na osi koordinat sostavlyayut

$R_{x} \equiv x = R\cos \alpha = {\displaystyle \frac{\displaystyle {\displaystyle k}}{\displaystyle {\displaystyle \sqrt {\displaystyle J} }}}\cos \alpha ,$

(2.38)

$R_{y} \equiv y = R\cos \beta = {\displaystyle \frac{\displaystyle {\displaystyle k}}{\displaystyle {\displaystyle \sqrt {\displaystyle J} }}}\cos \beta ,$

(2.39)

$R_{z} \equiv z = R\cos \gamma = {\displaystyle \frac{\displaystyle {\displaystyle k}}{\displaystyle {\displaystyle \sqrt {\displaystyle J} }}}\cos \gamma ,$

(2.40)

otkuda

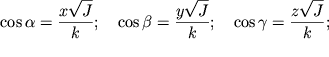$\cos \alpha = {\displaystyle \frac{\displaystyle {\displaystyle x\sqrt {\displaystyle J} }}{\displaystyle {\displaystyle k}}}; \quad \cos \beta = {\displaystyle \frac{\displaystyle {\displaystyle y\sqrt {\displaystyle J} }}{\displaystyle {\displaystyle k}}}; \quad \cos \gamma = {\displaystyle \frac{\displaystyle {\displaystyle z\sqrt {\displaystyle J} }}{\displaystyle {\displaystyle k}}};$

(2.41)

Podstavlyaya (2.41) v (2.35), poluchim

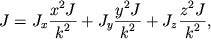$J = J_{x} {\displaystyle \frac{\displaystyle {\displaystyle x^{2}J}}{\displaystyle {\displaystyle k^{2}}}} + J_{y} {\displaystyle \frac{\displaystyle {\displaystyle y^{2}J}}{\displaystyle {\displaystyle k^{2}}}} + J_{z} {\displaystyle \frac{\displaystyle {\displaystyle z^{2}J}}{\displaystyle {\displaystyle k^{2}}}},$

(2.42)

ili

$J_{x} \cdot x^{2} + J_{y} \cdot y^{2} + J_{z} \cdot z^{2} = k^{2}.$

(2.43)

Eto, kak izvestno, uravnenie ellipsoida, kotoryi v dannom sluchae nazyvayut ellipsoidom inercii.

Centr ellipsoida inercii, kak vidno iz ego uravneniya, nahoditsya v nachale koordinat sistemy xyz (tochke O). Postoyannaya $k$ mozhet byt' vybrana proizvol'no i opredelyaet masshtab postroeniya; izmenyaya $k ,$ my budem poluchat' podobnye ellipsoidy. Glavnye osi ellipsoida inercii yavlyayutsya glavnymi osyami inercii tela dlya tochki O.

Ellipsoid inercii zhestko svyazan s telom, a ego polozhenie otnositel'no tela zavisit ot vybora tochki O. Ellipsoid inercii, postroennyi dlya centra mass tela, nazyvaetsya central'nym. Esli izvestno polozhenie ellipsoida inercii, izvestno i polozhenie vsego tela v dannyi moment vremeni. Rassmatrivaya vrashatel'noe dvizhenie tverdogo tela, v ryade sluchaev mozhno abstragirovat'sya ot ego formy i imet' delo s ellipsoidom inercii. Dlya kuba i shara, naprimer, central'nye ellipsoidy inercii vyrozhdayutsya v sferu, poetomu eti tela s tochki zreniya mnogih zadach mehaniki okazyvayutsya ekvivalentnymi.

Dlya primera rassmotrim sploshnoe odnorodnyi kub s rebrom $a$ i massoi $m$ . Ellipsoid inercii dlya centra odnoi iz granei kuba (tochka O) pokazan na ris. 2.14. Poluosi OA, OB, OS lezhat na glavnyh osyah inercii dlya tochki O, prichem OA = OB lezhat v ploskosti bokovoi grani, a $OC \approx 1,6 OA$ - perpendikulyarna bokovoi grani. Dlya sravneniya: ellipsoid inercii dlya centra kuba vyrozhdaetsya v sferu s radiusom, ravnym OS.

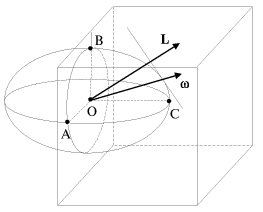Ris. 2.14.

Ponyatie ellipsoida inercii pozvolyaet s pomosh'yu dostatochno prostogo graficheskogo postroeniya ustanovit' svyaz' mezhdu uglovoi skorost'yu $\omega$ i momentom impul'sa L otnositel'no tochki O, prinadlezhashei osi vrasheniya. Rech' idet o tak nazyvaemom postroenii Puanso, kotoroe my privodim bez dokazatel'stva: neobhodimo postroit' ellipsoid inercii s centrom v tochke O i v tochke ego peresecheniya s os'yu vrasheniya (vektorom uglovoi skorosti $\omega$ ) ( provesti ploskost', kasatel'nuyu k ellipsoidu. Perpendikulyar, opushennyi iz centra ellipsoida inercii na kasatel'nuyu ploskost', i dast napravlenie vektora momenta impul'sa L Primer podobnogo postroeniya predstavlen na obsuzhdavshemsya vyshe ris. 2.14.

Nazad| Vpered

Publikacii s klyuchevymi slovami: mehanika - tverdoe telo - ugly Eilera Publikacii so slovami: mehanika - tverdoe telo - ugly Eilera
Sm. takzhe: Mehanika sploshnyh sred Variacionnye principy mehaniki Anizotropiya

Mneniya chitatelei [2]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce