Astronet > Mehanika tverdogo tela. Lekcii.

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Mehanika tverdogo tela. Lekcii.

V.A.Aleshkevich, L.G.Dedenko, V.A.Karavaev (Fizicheskii fakul'tet MGU)
Izdatel'stvo Fizicheskogo fakul'teta MGU, 1997 g. Soderzhanie

Vychislenie momentov inercii otnositel'no osi.

Pryamoi raschet momenta inercii tela otnositel'no osi svoditsya k vychisleniyu integrala

$J = \int {\displaystyle \rho ^{2}} \cdot dm,$

(2.44)

gde $\rho$ - rasstoyanie elementarnoi massy $dm$ do osi vrasheniya. Pri etom, estestvenno, neobhodimo uchityvat' simmetriyu sistemy.

Vychislim, k primeru, moment inercii shara (v sfericheskih koordinatah $r, \theta , \varphi ,$ ris. 2.15) otnositel'no proizvol'noi osi, prohodyashei cherez ego centr (v dannom sluchae otnositel'no osi Oz):

$dm = {\displaystyle \frac{\displaystyle {\displaystyle m}}{\displaystyle {\displaystyle V}}} \cdot dV = {\displaystyle \frac{\displaystyle {\displaystyle m}}{\displaystyle {\displaystyle V}}}r^{2}\sin \theta \cdot dr \cdot d\theta \cdot d\varphi ;$

(2.45)

$m$ - massa shara, $V$ - ego ob'em.

$\rho = r\sin \theta ,$

(2.46)

poetomu

$dJ = \rho ^{2} \cdot dm = {\displaystyle \frac{\displaystyle {\displaystyle m}}{\displaystyle {\displaystyle V}}}r^{4}\sin ^{3}\theta \cdot dr \cdot d\theta \cdot d\varphi ;$

(2.47)

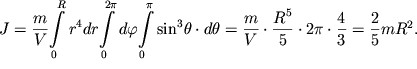$J = {\displaystyle \frac{\displaystyle {\displaystyle m}}{\displaystyle {\displaystyle V}}}{\displaystyle \int\limits_{0}^{R} {\displaystyle r^{4}} }dr{\displaystyle \int\limits_{0}^{2\pi } {\displaystyle d\varphi } }{\displaystyle \int\limits_{0}^{\pi } {\displaystyle \sin ^{3}} }\theta \cdot d\theta = {\displaystyle \frac{\displaystyle {\displaystyle m}}{\displaystyle {\displaystyle V}}} \cdot {\displaystyle \frac{\displaystyle {\displaystyle R^{5}}}{\displaystyle {\displaystyle 5}}} \cdot 2\pi \cdot {\displaystyle \frac{\displaystyle {\displaystyle 4}}{\displaystyle {\displaystyle 3}}} = {\displaystyle \frac{\displaystyle {\displaystyle 2}}{\displaystyle {\displaystyle 5}}}mR^{2}.$

(2.48)

Ris. 2.15.

Esli schitat', chto nasha Zemlya - shar s postoyannoi plotnost'yu massy, to moment inercii Zemli otnositel'no central'noi osi budet raven

$J_{Zemli} = 0,4 M_{Z} R_{Z}^{2} = 0,4 \cdot 0,6 \cdot 10^{24} kg \cdot \left( {\displaystyle 6,4 \cdot 10^{6} m} \right)^{2} \approx 10^{38} kg \cdot m^{2}.$

Dlya sravneniya rasschitaem moment inercii molekuly CO₂ otnositel'no osi, prohodyashei cherez atom ugleroda perpendikulyarno linii, vdol' kotoroi raspolozheny vse tri atoma (ris. 2.16).

Ris. 2.16.

Osnovnaya massa atomov sosredotochena v ih yadrah; razmery yader (~10^-14 m) znachitel'no men'she mezhyadernogo rasstoyaniya (~10^-10 m), poetomu atomy kisloroda mozhno schitat' material'nymi tochkami, a momentom inercii atoma ugleroda mozhno prenebrech'. Pri etih usloviyah $J_{CO_{2} } = 2{\displaystyle \frac{\displaystyle {\displaystyle \mu _{O_{2} } }}{\displaystyle {\displaystyle 2N_{A} }}} \cdot \ell ^{2},$ gde $\mu _{O_{2} }$ - molyarnaya massa kisloroda, $N_{A}$ - chislo Avogadro, $\ell$ - mezhyadernoe rasstoyanie (sm. ris. 2.16). Podstavlyaya chislovye znacheniya etih velichin, poluchim

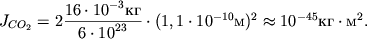$J_{CO_{2} } = 2{\displaystyle \frac{\displaystyle {\displaystyle 16 \cdot 10^{ - 3} kg}}{\displaystyle {\displaystyle 6 \cdot 10^{23}}}} \cdot (1,1 \cdot 10^{ - 10} m)^{2} \approx 10^{ - 45} kg \cdot m^{2}.$

Dlya ploskoi figury momenty inercii otnositel'no treh vzaimno perpendikulyarnyh osei, dve iz kotoryh lezhat v ploskosti figury, okazyvayutsya svyazannymi mezhdu soboi prostym sootnosheniem. Iz ris. 2.17 sleduet, chto

$dJ_{z} = \rho ^{2} \cdot dm = \left( {\displaystyle x^{2} + y^{2}} \right)dm = dJ_{y} + dJ_{x} ,$

(2.49)

otkuda

$J_{z} = J_{x} + J_{y}$

(2.50)

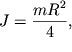Eto sootnoshenie pozvolyaet, naprimer, legko vychislit' moment inercii tonkogo diska massy $m$ i radiusa $R$ otnositel'no osi, prohodyashei cherez centr diska i lezhashei v ego ploskosti (lyubaya takaya os' budet glavnoi): $J = {\displaystyle \frac{\displaystyle {\displaystyle mR^{2}}}{\displaystyle {\displaystyle 4}}},$ poskol'ku moment inercii diska otnositel'no glavnoi central'noi osi, perpendikulyarnoi ploskosti diska, $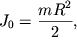J_{0} = {\displaystyle \frac{\displaystyle {\displaystyle mR^{2}}}{\displaystyle {\displaystyle 2}}},$ a $J_{0} = 2J.$

Ris. 2.17.

Teorema Gyuigecsa-Shteinera.

Eta teorema svyazyvaet momenty inercii otnositel'no dvuh parallel'nyh osei, odna iz kotoryh prohodit cherez centr mass tela.

Os' 1 na ris. 2.18 prohodit cherez centr mass O, os' 2 parallel'na ei; rasstoyanie mezhdu osyami ravno $a.$ $\bf R}_{i$ i $\rho_{i}$ - vektory, perpendikulyarnye osyam 1 i 2. Oni provedeny ot osei v tu tochku, gde raspolozhena massa $\Delta m_{i} .$

Ris. 2.18.

Moment inercii tela otnositel'no osi 2

$J = {\displaystyle \sum\limits_{i} {\displaystyle \Delta m_{i} } }\rho _{i}^{2} = {\displaystyle \sum\limits_{i} {\displaystyle \Delta m_{i} } }\left( {\displaystyle {\displaystyle \bf R}_{i} - {\displaystyle \bf a}} \right)^{2} = {\displaystyle \sum\limits_{i} {\displaystyle \Delta m_{i} } }R_{i}^{2} + {\displaystyle \sum\limits_{i} {\displaystyle \Delta m_{i} } }a^{2} - 2{\displaystyle \bf a}{\displaystyle \sum\limits_{i} {\displaystyle \Delta m_{i} } }{\displaystyle \bf R}_{i} .$

(2.51)

Poslednyaya summa ravna nulyu, poskol'ku os' 1 prohodit cherez centr mass, i

$J = J_{0} + ma^{2}.$

(2.52)

Esli, naprimer, os' - kasatel'naya k poverhnosti shara, to mozhno, ne provodya gromozdkih vychislenie, zapisat':

$J = J_{0} + mR^{2} = {\displaystyle \frac{\displaystyle {\displaystyle 2}}{\displaystyle {\displaystyle 5}}}mR^{2} + mR^{2} = {\displaystyle \frac{\displaystyle {\displaystyle 7}}{\displaystyle {\displaystyle 5}}}mR^{2}.$

(2.53)

Moment impul'sa tela otnositel'no dvizhushegosya centra mass.

Do sih por, rassmatrivaya moment impul'sa tverdogo tela, my opredelyali ego otnositel'no nekotoroi nepodvizhnoi v laboratornoi sisteme XYZ tochki (naprimer, tochki zakrepleniya tela). Vo mnogih zadachah dinamiki eto okazyvaetsya neudobno. Naprimer, reshaya zadachu o diske, skatyvayushemsya s naklonnoi ploskosti, logichno rassmatrivat' moment impul'sa diska otnositel'no ego centra mass, a ne otnositel'no tochki, prinadlezhashei naklonnoi ploskosti.

Rassmotrim, kak budut svyazany momenty impul'sa tela, opredelennye otnositel'no nekotoroi nepodvizhnoi tochki O' i otnositel'no centra mass tela O, dvizhushegosya proizvol'nym obrazom (ris. 2.19).

Ris. 2.19.

Pust' ${\displaystyle \bf r}}'_{i$ i $\bf }r_{i$ - radiusy-vektory elementarnoi massy $\Delta m_{i}$ - tela otnositel'no tochek O' i O, R - radius-vektor, provedennyi iz O' v O. Eti vektory svyazany mezhdu soboi ochevidnym sootnosheniem

${\displaystyle \bf r}}'_{i} = {\displaystyle \bf R} + {\displaystyle \bf r}_{i$

(2.54)

Moment impul'sa tela otnositel'no tochki O' (sm. formulu (2.1))

${\displaystyle \bf L}_{O'} = {\displaystyle \sum\limits_{i} {\displaystyle {\displaystyle {\displaystyle \bf r}}'_{i} } }\times \Delta m_{i} {\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle {\displaystyle \bf r}}'_{i} }}{\displaystyle {\displaystyle dt}}} = {\displaystyle \sum\limits_{i} {\displaystyle {\displaystyle \left[ {\displaystyle \left( {\displaystyle {\displaystyle \bf R} + {\displaystyle \bf r}_{i} } \right)\times \Delta m_{i} \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle \bf R}}}{\displaystyle {\displaystyle dt}}} + {\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle \bf r}_{i} }}{\displaystyle {\displaystyle dt}}}} \right)} \right]}} }.$

(2.55)

Vospol'zuemsya ochevidnymi ravenstvami

${\displaystyle \sum\limits_{i} {\displaystyle \Delta m_{i} } } = M$

(2.56)

( $M$ - massa vsego tela);

${\displaystyle \sum\limits_{i} {\displaystyle \Delta m_{i} } }{\displaystyle \bf r}_{i} = 0$

(2.57)

${\displaystyle \sum\limits_{i} {\displaystyle \Delta m_{i} } }{\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle \bf r}_{i} }}{\displaystyle {\displaystyle dt}}} = 0,$

(2.58)

poskol'ku tochka O sovpadaet s centrom mass tela. S uchetom (2.56 - 2.58) iz (2.55) poluchim

${\displaystyle \bf L}_{O'} = {\displaystyle \bf R}\times M{\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle \bf R}}}{\displaystyle {\displaystyle dt}}} + {\displaystyle \sum\limits_{i} {\displaystyle {\displaystyle \bf r}_{i} } }\times \Delta m_{i} {\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle \bf r}_{i} }}{\displaystyle {\displaystyle dt}}} = {\displaystyle \bf R}\times {\displaystyle \bf p} + {\displaystyle \sum\limits_{i} {\displaystyle {\displaystyle \bf r}_{i} } }\times \Delta m_{i} {\displaystyle \bf v}_{i} ,$

(2.59)

gde $\bf p} = M{\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle \bf R}}}{\displaystyle {\displaystyle dt}}$ - polnyi impul's tela v laboratornoi sisteme XYZ, $\bf v}_{i$ - skorost' i-oi massy otnositel'no centra mass.

Esli moment impul'sa tela otnositel'no ego centra mass (otnositel'nyi moment impul'sa) opredelit' kak

${\displaystyle \bf L}_{O} = {\displaystyle \sum\limits_{i} {\displaystyle {\displaystyle \bf r}_{i} } }\times \Delta m_{i} {\displaystyle \bf v}_{i} ,$

(2.60)

to iz (2.59) sleduet iskomoe sootnoshenie

${\displaystyle \bf L}_{O'} = {\displaystyle \bf L}_{O} + {\displaystyle \bf R}\times {\displaystyle \bf p}.$

(2.61)

Eshe raz podcherknem, chto pri opredelenii momenta impul'sa tela otnositel'no ego centra mass (velichina ${\displaystyle \bf L}_O$ (sleduet brat' otnositel'nye skorosti vseh tochek tela, to est' skorosti tochek tela otnositel'no centra mass, schitaya ego kak by nepodvizhnym.

Zamechanie. Sootnoshenie (2.61) pozvolyaet takzhe svyazat' momenty impul'sa otnositel'no dvuh parallel'nyh osei, odna iz kotoryh nepodvizhna, a drugaya prohodit cherez centr mass dvizhushegosya tela.

Obratimsya k primeram.

1. Moment impul'sa cilindra, skatyvayushegosya bez proskal'zyvaniya s naklonnoi ploskosti, otnositel'no ego osi raven $J_{0} \omega$ ( $J_{0}$ - moment inercii cilindra otnositel'no ego osi, $\omega$ - mgnovennaya uglovaya skorost' vrasheniya cilindra). Moment impul'sa togo zhe cilindra otnositel'no mgnovennoi osi vrasheniya, prohodyashei cherez tochku kasaniya cilindra i ploskosti, budet raven $J_{0} \omega + Rmv_{0} = J_{0} \omega + Rm\left( {\displaystyle \omega R} \right) = \left( {\displaystyle J_{0} + mR^{2}} \right)\omega = J\omega ,$ gde $J$ - moment inercii cilindra otnositel'no mgnovennoi osi vrasheniya, $R$ - radius cilindra.

2. Esli sharu massy $m$ soobshit' skorost' ${\displaystyle \bf v}_{0} ,$ obespechivayushuyu dvizhenie po krugovoi orbite vokrug gravitacionnogo silovogo centra O', to on budet dvigat'sya postupatel'no $\left( L_{O} = 0 \right),$ a ego moment impul'sa otnositel'no O' $L_{O'} = mv_{0} R$ (ris. 2.20a). Esli pri etom shar budet vrashat'sya vokrug sobstvennoi osi s uglovoi skorost'yu $\omega ,$ kak pokazano na ris. 2.20b, to postoyannyi otnositel'no tochki O' moment impul'sa shara budet raven $L_{O'} = L_{O} + mv_{0} R = J_{0} \omega + mv_{0} R.$

Ris. 2.20.

Raschety pokazyvayut, chto moment impul'sa planet Solnechnoi sistemy otnositel'no sobstvennogo centra mass znachitel'no men'she ih orbital'nogo momenta impul'sa. Orbity vseh planet lezhat priblizitel'no v odnoi ploskosti, tak chto ih orbital'nye momenty impul'sa skladyvayutsya arifmeticheski. Interesno, chto vse 9 planet dvizhutsya vokrug Solnca v odnom i tom zhe napravlenii, tak chto summarnyi moment impul'sa Solnechnoi sistemy otlichen ot nulya.

Nazad| Vpered

Publikacii s klyuchevymi slovami: mehanika - tverdoe telo - ugly Eilera Publikacii so slovami: mehanika - tverdoe telo - ugly Eilera
Sm. takzhe: Mehanika sploshnyh sred Variacionnye principy mehaniki Anizotropiya

Mneniya chitatelei [2]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce