Astronet > Mehanika tverdogo tela. Lekcii.

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Mehanika tverdogo tela. Lekcii.

V.A.Aleshkevich, L.G.Dedenko, V.A.Karavaev (Fizicheskii fakul'tet MGU)
Izdatel'stvo Fizicheskogo fakul'teta MGU, 1997 g. Soderzhanie

Lekciya 3.

Dinamika absolyutno tverdogo tela. Uravnenie postupatel'nogo dvizheniya i uravnenie momentov. Vrashenie tverdogo tela vokrug nepodvizhnoi osi. Centr udara. Dinamika ploskogo dvizheniya tverdogo tela. Dvizhenie aksial'no simmetrichnogo tverdogo tela, zakreplennogo v centre mass. Uravneniya Eilera.

Uravneniya dinamiki tverdogo tela. Obshii sluchai.

V obshem sluchae absolyutno tverdoe telo imeet 6 stepenei svobody, i dlya opisaniya ego dvizheniya neobhodimy 6 nezavisimyh skalyarnyh uravnenii ili 2 nezavisimyh vektornyh uravneniya.

Vspomnim, chto tverdoe telo mozhno rassmatrivat' kak sistemu material'nyh tochek, i, sledovatel'no, k nemu primenimy te uravneniya dinamiki, kotorye spravedlivy dlya sistemy tochek v celom.

Obratimsya k opytam.

Voz'mem rezinovuyu palku, utyazhelennuyu na odnom iz koncov i imeyushuyu lampochku tochno v centre mass (ris. 3.1). Zazhzhem lampochku i brosim palku iz odnogo konca auditorii v drugoi, soobshiv ei proizvol'noe vrashenie - traektoriei lampochki budet pri etom parabola - krivaya, po kotoroi poletelo by nebol'shoe telo, broshennoe pod uglom k gorizontu.

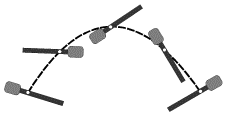Ris. 3.1.

Sterzhen', opirayushiisya odnim iz koncov na gladkuyu gorizontal'nuyu ploskost' (ris.1.16), padaet takim obrazom, chto ego centr mass ostaetsya na odnoi i toi zhe vertikali - net sil, kotorye sdvinuli by centr mass sterzhnya v gorizontal'nom napravlenii.

Opyt, kotoryi byl predstavlen na ris. 2.2 a, v, svidetel'stvuet o tom, chto dlya izmeneniya momenta impul'sa tela sushestvenna ne prosto sila, a ee moment otnositel'no osi vrasheniya.

Telo, podveshennoe v tochke, ne sovpadayushei s ego centrom mass (fizicheskii mayatnik), nachinaet kolebat'sya (ris. 3.2a) - est' moment sily tyazhesti otnositel'no tochki podvesa, vozvrashayushii otklonennyi mayatnik v polozhenie ravnovesiya. No tot zhe mayatnik, podveshennyi v centre mass, nahoditsya v polozhenii bezrazlichnogo ravnovesiya (ris. 3.2b).

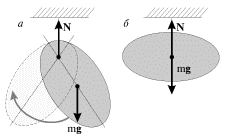Ris. 3.2.

Rol' momenta sily naglyadno proyavlyaetsya v opytah s "poslushnoi" i "neposlushnoi" katushkami (ris. 3.3). Ploskoe dvizhenie etih katushek mozhno predstavit' kak chistoe vrashenie vokrug mgnovennoi osi, prohodyashee cherez tochku soprikosnoveniya katushki s ploskost'yu. V zavisimosti ot napravleniya momenta sily F otnositel'no mgnovennoi osi katushka libo otkatyvaetsya (ris. 3.Za), libo nakatyvaetsya na nitku (ris. 3.Zb). Derzha nit' dostatochno blizko k gorizontal'noi ploskosti, mozhno prinudit' k poslushaniyu samuyu "neposlushnuyu" katushku.

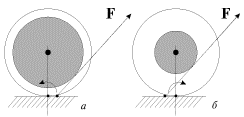Ris. 3.3.

Vse eti opyty vpolne soglasuyutsya s izvestnymi zakonami dinamiki, sformulirovannymi dlya sistemy material'nyh tochek: zakonom dvizheniya centra mass i zakonom izmeneniya momenta impul'sa sistemy pod deistviem momenta vneshnih sil. Takim obrazom, v kachestve dvuh vektornyh uravnenii dvizheniya tverdogo tela mozhno ispol'zovat':

Uravnenie dvizheniya centra mass

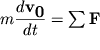$m{\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle \bf v}_{{\displaystyle \bf 0}} }}{\displaystyle {\displaystyle dt}}} = \sum {\displaystyle {\displaystyle \bf F}}$

(3.1)

Zdes' $\bf v}_{{\displaystyle \bf 0}$ - skorost' centra mass tela, $\sum {\displaystyle {\displaystyle \bf F}}$ - summa vseh vneshnih sil, prilozhennyh k telu.

Uravnenie momentov

$\frac{\displaystyle {\displaystyle d{\displaystyle \bf L}}}{\displaystyle {\displaystyle dt}}} = \sum {\displaystyle {\displaystyle \bf M}$

(3.2)

Zdes' L- moment impul'sa tverdogo tela otnositel'no nekotoroi tochki, $\sum {\displaystyle {\displaystyle \bf M}}$ - summarnyi moment vneshnih sil otnositel'no toi zhe samoi tochki.

K uravneniyam (3.1) i (3.2), yavlyayushimsya uravneniyami dinamiki tverdogo tela, neobhodimo dat' sleduyushie kommentarii:

1. Vnutrennie sily, kak i v sluchae proizvol'noi sistemy material'nyh tochek, ne- vliyayut na dvizhenie centra mass i ne mogut izmenit' moment impul'sa tela.

2. Tochku prilozheniya vneshnei sily mozhno proizvol'no peremeshat' vdol' linii, po kotoroi deistvuet sila. Eto sleduet iz togo, chto v modeli absolyutno tverdogo tela lokal'nye deformacii, voznikayushie v oblasti prilozheniya sily, v raschet ne prinimayutsya. Ukazannyi perenos ne povliyaet i na moment sily otnositel'no kakoi by to ni bylo tochki, tak kak plecho sily pri etom ne izmenitsya.

Vektory L i M v uravnenii (3.2), kak pravilo, rassmatrivayutsya otnositel'no nekotoroi nepodvizhnoi v laboratornoi sisteme XYZ tochki. Vo mnogih zadachah L i M udobno rassmatrivat' otnositel'no dvizhushegosya centra mass tela. V etom sluchae uravnenie momentov imeet vid, formal'no sovpadayushii s (3.2). V samom dele, moment impul'sa tela $\bf L}_{0$ otnositel'no dvizhushegosya centra .mass O svyazan s momentom impul'sa $\bf L}_{{\displaystyle 0}'$ otnositel'no nepodvizhnoi - tochki O' sootnosheniem, poluchennym v konce lekcii 2:

${\displaystyle \bf L}_{0} = {\displaystyle \bf L}_{{\displaystyle 0}'} - {\displaystyle \bf R}\times {\displaystyle \bf p},$

(3.3)

gde R - radius-vektor ot O' k O, p - polnyi impul's tela. Analogichnoe sootnoshenie legko mozhet byt' polucheno i dlya momentov sily:

${\displaystyle \bf M}_{0} = {\displaystyle \bf M}_{{\displaystyle 0}'} - {\displaystyle \bf R}\times {\displaystyle \bf F},$

(3.4)

gde F - geometricheskaya summa vseh sil, deistvuyushih na tverdoe telo.

Poskol'ku tochka O' nepodvizhna, to spravedlivo uravnenie momentov (3.2):

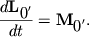${\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle \bf L}_{{\displaystyle 0}'} }}{\displaystyle {\displaystyle dt}}} = {\displaystyle \bf M}_{{\displaystyle 0}'} .$

(3.5)

Togda

$\frac{\displaystyle {\displaystyle d{\displaystyle \bf L}_{0} }}{\displaystyle {\displaystyle dt}}} = \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle \bf L}_{{\displaystyle 0}'} }}{\displaystyle {\displaystyle dt}}} - {\displaystyle \bf R}\times {\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle \bf p}}}{\displaystyle {\displaystyle dt}}}} \right) - {\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle \bf R}}}{\displaystyle {\displaystyle dt}}}\times {\displaystyle \bf p} = \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle \bf L}_{{\displaystyle 0}'} }}{\displaystyle {\displaystyle dt}}} - {\displaystyle \bf R}\times {\displaystyle \bf F}} \right) - {\displaystyle \bf v}_{{\displaystyle \bf 0}} \times {\displaystyle \bf p$

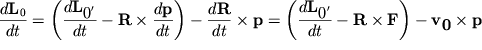(3.6)

Zdes' uchteno, chto {\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle \bf p}}}{\displaystyle {\displaystyle dt}}} = {\displaystyle \bf F}.

Velichina $\bf v}_{{\displaystyle \bf 0}} = {\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle \bf R}}}{\displaystyle {\displaystyle dt}}$ est' skorost' tochki O v laboratornoi sisteme XYZ. Uchityvaya (3.4), poluchim

${\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle \bf L}_{0} }}{\displaystyle {\displaystyle dt}}} = {\displaystyle \bf M}_{0} - {\displaystyle \bf v}_{{\displaystyle \bf 0}} \times {\displaystyle \bf p}.$

(3.7)

Poskol'ku dvizhushayasya tochka O - eto centr mass tela, to $\bf p} = m{\displaystyle \bf v}_{{\displaystyle \bf 0}$ ( $m$ - massa tela), ${\displaystyle \bf v}_{{\displaystyle \bf 0}} \times {\displaystyle \bf p} = 0$ i ${\displaystyle \frac{\displaystyle {\displaystyle d{\displaystyle \bf L}_{0} }}{\displaystyle {\displaystyle dt}}} = {\displaystyle \bf M}_{0} ,$ to est' uravnenie momentov otnositel'no dvizhushegosya centra mass imeet takoi zhe vid, chto i otnositel'no nepodvizhnoi tochki. Sushestvenno otmetit', chto v etom sluchae, kak bylo pokazano v konce lekcii 2, skorosti vseh tochek tela pri opredelenii $\bf L}_{0$ sleduet brat' otnositel'no centra mass tela.

Ranee bylo pokazano, chto proizvol'noe dvizhenie tverdogo tela mozhno razlozhit' na postupatel'noe (vmeste s sistemoi x₀y₀z₀, nachalo kotoroi nahoditsya v nekotoroi tochke - polyuse, zhestko svyazannoi s telom) i vrashatel'noe (vokrug mgnovennoi osi, prohodyashei cherez polyus). S tochki zreniya kinematiki vybor polyusa osobogo znacheniya ne imeet, s tochki zhe zreniya dinamiki polyus, kak teper' ponyatno, udobno pomestit' v centr mass. Imenno v etom sluchae uravnenie momentov (3.2) mozhet byt' zapisano otnositel'no centra mass (ili osi, prohodyashei cherez centr mass) kak otnositel'no nepodvizhnogo nachala (ili nepodvizhnoe osi).

Esli $\sum {\displaystyle {\displaystyle \bf F}}$ ne zavisit ot uglovoi skorosti tela, a $\sum {\displaystyle {\displaystyle \bf M}}$ - ot skorosti centra mass, to uravneniya (3.1) i (3.2) mozhno rassmatrivat' nezavisimo drug ot druga. V etom sluchae uravnenie (3.1) sootvetstvuet prosto zadache iz mehaniki tochki, a uravnenie (3.2) - zadache o vrashenii tverdogo tela vokrug nepodvizhnoi tochki ili nepodvizhnoi osi. Primer situacii, kogda uravneniya (3.1) i (3.2) nel'zya rassmatrivat' nezavisimo - dvizhenie vrashayushegosya tverdogo tela v vyazkoi srede.

Dalee v etoi lekcii my rassmotrim uravneniya dinamiki dlya treh chastnyh sluchaev dvizheniya tverdogo tela: vrasheniya vokrug nepodvizhnoi osi, ploskogo dvizheniya i, nakonec, dvizheniya tverdogo tela, imeyushego os' simmetrii i zakreplennogo v centre mass.

Nazad| Vpered

Publikacii s klyuchevymi slovami: mehanika - tverdoe telo - ugly Eilera Publikacii so slovami: mehanika - tverdoe telo - ugly Eilera
Sm. takzhe: Mehanika sploshnyh sred Variacionnye principy mehaniki Anizotropiya

Mneniya chitatelei [2]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce