Kolebaniya i volny. Lekcii.
V.A.Aleshkevich, L.G.Dedenko, V.A.Karavaev (Fizicheskii fakul'tet MGU)Izdatel'stvo Fizicheskogo fakul'teta MGU, 2001 g. Soderzhanie
Vynuzhdennye kolebaniya s proizvol'noi chastotoi.
Budem iskat' reshenie uravneniya (2.10) v kompleksnom vide:
| (2.26) |
Vynuzhdayushuyu silu v pravoi chasti (2.10) takzhe zapishem v kompleksnoi forme:
| (2.27) |
gde ![]() - deistvitel'noe chislo, poskol'ku dlya prostoty
my polozhili, chto nachal'naya faza v vyrazhenii dlya sily (2.5) ravna nulyu.
- deistvitel'noe chislo, poskol'ku dlya prostoty
my polozhili, chto nachal'naya faza v vyrazhenii dlya sily (2.5) ravna nulyu.
Togda uravnenie (2.10) mozhno zapisat' v vide:
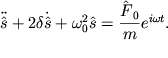 | (2.28) |
Kompleksnuyu amplitudu ![]() legko
nahodim podstanovkoi (2.26) v (2.28):
legko
nahodim podstanovkoi (2.26) v (2.28):
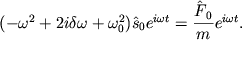 | (2.29) |
Otsyuda poluchaem:
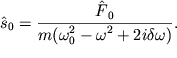 | (2.30) |
Iz (2.30) netrudno naiti amplitudu kolebanii ![]()
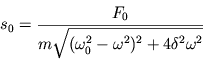 | (2.31) |
i fazu ![]()
| (2.32) |
polnost'yu opredelyayushie vynuzhdennye kolebaniya (2.25).
Zavisimost' amplitudy ![]() ot chastoty
ot chastoty ![]() zadavaemaya formuloi
(2.31), nazyvaetsya amplitudno-chastotnoi harakteristikoi (AChH), a
zavisimost'
zadavaemaya formuloi
(2.31), nazyvaetsya amplitudno-chastotnoi harakteristikoi (AChH), a
zavisimost' ![]() opisyvaemaya formuloi (2.32),
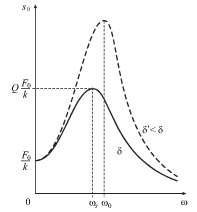
nazyvaetsya fazo-chastotnoi harakteristikoi (FChH). Na ris. 2.3 izobrazhena
AChH, kotoraya otobrazhaet narastanie amplitudy
opisyvaemaya formuloi (2.32),
nazyvaetsya fazo-chastotnoi harakteristikoi (FChH). Na ris. 2.3 izobrazhena
AChH, kotoraya otobrazhaet narastanie amplitudy ![]() pri priblizhenii
pri priblizhenii ![]() k
k ![]() Eto yavlenie poluchilo nazvanie rezonansa smeshenii.
Interesno, chto maksimal'noe znachenie amplitudy, v
Eto yavlenie poluchilo nazvanie rezonansa smeshenii.
Interesno, chto maksimal'noe znachenie amplitudy, v ![]() raz prevoshodyashee
staticheskoe smeshenie
raz prevoshodyashee
staticheskoe smeshenie ![]() dostigaetsya na chastote
dostigaetsya na chastote
| (2.33) |
kotoraya neskol'ko men'she kak sobstvennoi chastoty ![]() tak i
chastoty zatuhayushih kolebanii
tak i
chastoty zatuhayushih kolebanii ![]() Dlya
prakticheskih celei dlya chastot
Dlya
prakticheskih celei dlya chastot ![]() lezhashih vblizi chastoty
lezhashih vblizi chastoty ![]() formula (2.31) mozhet byt' znachitel'no uproshena. Tak, mozhno polozhit'
formula (2.31) mozhet byt' znachitel'no uproshena. Tak, mozhno polozhit'
| (2.34) | |
 |
| Ris. 2.3. |
S uchetom priblizhenii (2.34) formula (2.31) primet vid:
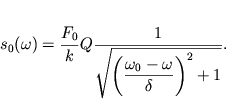 | (2.35) |
V fizike bezrazmernuyu funkciyu
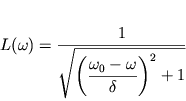 | (2.36) |
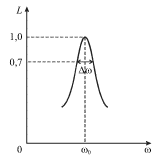
nazyvayut Lorencevoi, a grafik etoi funkcii nazyvayut Lorencevym konturom.
Shirinu ![]() etogo kontura, opredelyayushuyu ostrotu rezonansa,
nahodyat iz usloviya ubyvaniya vdvoe energii kolebatel'noi sistemy,
proporcional'noi kvadratu amplitudy
etogo kontura, opredelyayushuyu ostrotu rezonansa,
nahodyat iz usloviya ubyvaniya vdvoe energii kolebatel'noi sistemy,
proporcional'noi kvadratu amplitudy ![]() v (2.35), chto
ekvivalentno priblizhennomu sootnosheniyu
v (2.35), chto
ekvivalentno priblizhennomu sootnosheniyu
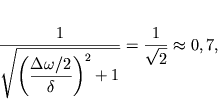 | (2.37) |
kotoroe poyasnyaetsya risunkom 2.4. Pri etom uslovii ![]() t.e.
t.e. ![]() Shirina Lorenceva
kontura harakterizuet polosu propuskaniya kolebatel'noi sistemy, t.e. takuyu
oblast' chastot vneshnei sily, dlya kotoryh sistema effektivno otklikaetsya na
garmonicheskoe vneshnee vozdeistvie. Legko videt', chto dobrotnost' sistemy
ravna
Shirina Lorenceva
kontura harakterizuet polosu propuskaniya kolebatel'noi sistemy, t.e. takuyu
oblast' chastot vneshnei sily, dlya kotoryh sistema effektivno otklikaetsya na
garmonicheskoe vneshnee vozdeistvie. Legko videt', chto dobrotnost' sistemy
ravna
| (2.38) |
t.e. obratno proporcional'na polose propuskaniya.
 |
| Ris. 2.4. |
S umen'sheniem koefficienta ![]() AChH menyaet svoyu formu, kak eto
izobrazheno punktirom na ris. 2.3 dlya
AChH menyaet svoyu formu, kak eto
izobrazheno punktirom na ris. 2.3 dlya ![]() Polosa
propuskaniya
Polosa
propuskaniya ![]() umen'shaetsya, dobrotnost'
umen'shaetsya, dobrotnost' ![]() vozrastaet, i
rezonans stanovitsya bolee ostrym.
vozrastaet, i
rezonans stanovitsya bolee ostrym.
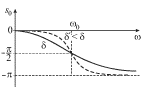
Fazo-chastotnaya harakteristika dlya dvuh razlichnyh koefficientov zatuhaniya
izobrazhena na ris. 2.5. Fizicheskoe soderzhanie zavisimosti ![]() my podrobno obsudili dlya treh razlichnyh rezhimov vynuzhdennyh
kolebanii. Otmetim lish', chto s umen'sheniem zatuhaniya
my podrobno obsudili dlya treh razlichnyh rezhimov vynuzhdennyh
kolebanii. Otmetim lish', chto s umen'sheniem zatuhaniya ![]() krivaya
krivaya
![]() stanovitsya bolee "chuvstvitel'noi" k izmeneniyu
chastoty vblizi rezonansa.
stanovitsya bolee "chuvstvitel'noi" k izmeneniyu
chastoty vblizi rezonansa.
 |
| Ris. 2.5. |
Naryadu s rezonansom smeshenii, mozhno govorit' o rezonanse skorostei ![]() i rezonanse uskorenii
i rezonanse uskorenii ![]()
Skorost' koleblyusheisya massy ravna:
| (2.39) |
a ee uskorenie:
| (2.40) |
t.e. amplitudno-chastotnaya harakteristika dlya skorosti poluchaetsya umnozheniem
AChH (2.31) na ![]() a dlya uskoreniya - na
a dlya uskoreniya - na ![]() :
:
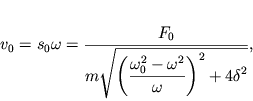 |
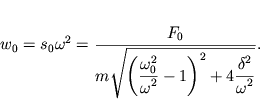 |
Na ris. 2.6 izobrazheny chastotnye zavisimosti amplitud skorosti ![]() i uskoreniya
i uskoreniya ![]()
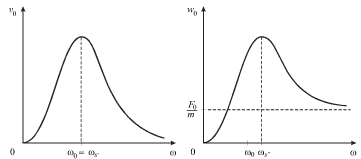 |
| Ris. 2.6. |
Harakterno, chto rezonans skorosti proishodit na chastote ![]() a rezonans uskoreniya - pri
a rezonans uskoreniya - pri ![]() Otmetim, chto vse rezonansnye chastoty svyazany mezhdu soboi:
Otmetim, chto vse rezonansnye chastoty svyazany mezhdu soboi:
| (2.41) |
Otmetim takzhe, chto po prichinam, rassmotrennym ranee, v oblasti nizkih chastot
maly kak uskorenie, tak i skorost'. V oblasti vysokih chastot uskorenie
konechno ![]() i obespechivaetsya lish'
vneshnei siloi. Odnako skorost' po-prezhnemu neznachitel'na, poskol'ku telo ne
uspevaet razognat'sya.
i obespechivaetsya lish'
vneshnei siloi. Odnako skorost' po-prezhnemu neznachitel'na, poskol'ku telo ne
uspevaet razognat'sya.
Ne predstavlyaet truda narisovat' samostoyatel'no fazo-chastotnye
harakteristiki dlya skorosti i dlya uskoreniya, pol'zuyas' formulami (2.39) i
(2.40), poskol'ku oni poluchayutsya prostym sdvigom FChH dlya smesheniya (2.32),
izobrazhennoi na ris. 2.5, vverh sootvetstvenno na ![]() ili na
ili na ![]()
V zaklyuchenie rassmotrim vopros o podvode energii k oscillyatoru pri proizvol'noi chastote vynuzhdayushei sily. Srednyaya za period moshnost' etoi sily ravna
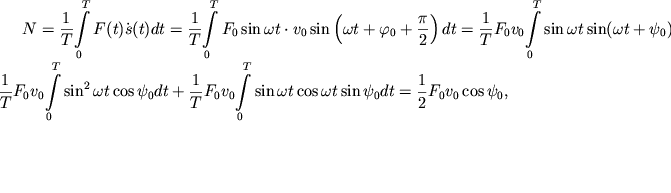 |
gde ![]() - sdvig faz mezhdu skorost'yu i siloi. My vidim, chto maksimum podvodimoi k oscillyatoru moshnosti
dostigaetsya na chastote
- sdvig faz mezhdu skorost'yu i siloi. My vidim, chto maksimum podvodimoi k oscillyatoru moshnosti
dostigaetsya na chastote ![]() poskol'ku pri etom maksimal'ny i
amplituda skorosti
poskol'ku pri etom maksimal'ny i
amplituda skorosti ![]() i
i ![]() Pri drugih
chastotah vynuzhdayushei sily eta moshnost' bystro umen'shaetsya i stremitsya k
nulyu, kak pri
Pri drugih
chastotah vynuzhdayushei sily eta moshnost' bystro umen'shaetsya i stremitsya k
nulyu, kak pri ![]() tak i pri
tak i pri ![]()
|
Publikacii s klyuchevymi slovami:
kolebaniya - volny
Publikacii so slovami: kolebaniya - volny | |
|
Sm. takzhe:
| |