Astronet > Kolebaniya i volny

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Kolebaniya i volny. Lekcii.

V.A.Aleshkevich, L.G.Dedenko, V.A.Karavaev (Fizicheskii fakul'tet MGU)
Izdatel'stvo Fizicheskogo fakul'teta MGU, 2001 g. Soderzhanie

Ballisticheskii rezhim kolebanii.

Rassmotrim kolebaniya sistemy, k kotoroi prilozhena proizvol'naya sila $F(t),$ deistvuyushaya v techenie promezhutka vremeni $\Delta t,$ znachitel'no men'shego perioda sobstvennyh kolebanii: $\Delta t \ll T.$ Otklik sistemy na takoe vozdeistvie budet proporcionalen impul'su deistvuyushei sily:

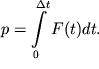$p = {\displaystyle \int\limits_{0}^{\Delta t} {\displaystyle F(t)dt.} }$

(2.42)

V samom dele, pri kratkovremennom vozdeistvii (v techenie vremeni $\Delta t)$ mayatnik ne uspevaet zametno smestit'sya iz polozheniya ravnovesiya, odnako budet obladat' uskoreniem

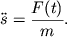$\ddot {\displaystyle s} = {\displaystyle \frac{\displaystyle {\displaystyle F(t)}}{\displaystyle {\displaystyle m}}}.$

(2.43)

Pri zapisi (2.43) my prenebregli siloi vyazkogo treniya. Po okonchanii deistviya sily mayatnik priobretet skorost'

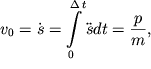$v_{0} = \dot {\displaystyle s} = {\displaystyle \int\limits_{0}^{\Delta \,t} {\displaystyle \ddot {\displaystyle s}dt} } = {\displaystyle \frac{\displaystyle {\displaystyle p}}{\displaystyle {\displaystyle m}}},$

(2.44)

proporcional'nuyu impul'su sily.

Dalee mayatnik budet sovershat' sobstvennye garmonicheskie kolebaniya s amplitudoi

$s_{0} = {\displaystyle \frac{\displaystyle {\displaystyle v_{0} }}{\displaystyle {\displaystyle \omega _{0} }}} = {\displaystyle \frac{\displaystyle {\displaystyle p}}{\displaystyle {\displaystyle m\omega _{0} }}}.$

(2.45)

Esli parametry $m$ i $\omega _{0}$ izvestny, to izmeryaya amplitudu pervogo kolebaniya posle vozdeistviya, mozhno opredelit' $p.$

V kachestve primera rassmotrim proceduru izmereniya zaryada, protekayushego po elektricheskoi cepi, s ispol'zovaniem ballisticheskogo gal'vanometra. Etot gal'vanometr soderzhit ramku, kotoraya mozhet sovershat' krutil'nye kolebaniya. Ramka imeet uvelichennyi (po sravneniyu s obychnym gal'vanometrom) moment inercii, chto uvelichivaet period ee sobstvennyh kolebanii do neskol'kih sekund. T.k. ramka nahoditsya v magnitnom pole postoyannogo magnita, to pri protekanii cherez nee elektricheskogo toka na ramku budet deistvovat' moment sil, proporcional'nyi toku. Pri protekanii kratkovremennogo toka ramka priobretaet uglovuyu skorost' i zatem za chetvert' perioda kolebanii otklonyaetsya na nekotoryi maksimal'nyi ugol, kotoryi proporcionalen integralu ot protekshego cherez ramku toka, t.e. velichine protekshego zaryada.

Ustanovlenie kolebanii.

My uzhe otmechali, chto esli prilozhit' k pokoyashemusya mayatniku garmonicheskuyu silu v moment vremeni $t = 0,$ to mayatnik nachnet postepenno raskachivat'sya, kak eto kachestvenno izobrazheno na ris. 2.7a. Ustanovlenie kolebanii svyazano s tem faktom, chto naryadu s vynuzhdennymi kolebaniyami na chastote $\omega$ budut vozbuzhdeny i sobstvennye kolebaniya na chastote $\sqrt {\displaystyle \omega _{0}^{2} - \delta ^{2}},$ kotorye, konechno, budut zatuhat'.

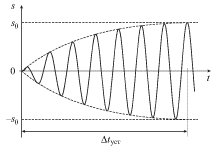Ris. 2.7a.

Iz matematiki izvestno, chto obshee reshenie lineinogo neodnorodnogo uravneniya (2.10) pri $\delta \lt \omega _{0}$ imeet vid:

$s(t) = s_{0c} e^{ - \delta t}\sin (\sqrt {\displaystyle \omega _{0}^{2} - \delta ^{2}} t + \varphi _{c} ) + s_{0} \sin (\omega t + \varphi _{0} ),$

(2.50)

predstavlyayushii soboi superpoziciyu sobstvennyh zatuhayushih kolebanii na chastote $\sqrt {\displaystyle \omega _{0}^{2} - \delta ^{2}}$ i nezatuhayushih vynuzhdennyh kolebanii na chastote $\omega .$ Iz (2.50) vidno, chto kolebaniya ustanovyatsya lish' togda, kogda zatuhnut sobstvennye kolebaniya. Eto proizoidet po istechenii vremeni

$\Delta t_{ust} \sim \tau = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle \delta }}}.$

(2.51)

Za eto vremya v sistemu "zakachivaetsya" energiya, poskol'ku do ustanovleniya kolebanii rabota vneshnei sily prevyshaet rabotu sil treniya. V ustanovivshemsya rezhime imeet mesto balans postupayushei i rashoduemoi energii.

V chastnosti, esli $\omega = \sqrt {\displaystyle \omega _{0}^{2} - \delta ^{2}} ,$ to (2.50) pri $s(0) = 0, \dot {\displaystyle s}(0) = 0$ i $\delta \ll \omega _{0} ,$ kak netrudno pokazat', imeet vid

$s(t) = s_{0} (1 - e^{ - \delta t})\sin (\omega t - \pi / 2),$

(2.52)

poskol'ku pri etih usloviyah $s_{0c} = s_{0} , \varphi _{c} = - \varphi _{0} \approx {\displaystyle \frac{\displaystyle {\displaystyle \pi }}{\displaystyle {\displaystyle 2}}}.$

Otmetim, chto formula (2.51) opredelyaet lish' poryadok velichiny (vremennoi masshtab) $\Delta t_{ust} .$ Dlya prakticheskih celei vremya ustanovleniya (ravno kak i vremya zatuhaniya) kolebanii prinimayut ravnym $\Delta t_{ust} = (3\div 5)\tau .$

Na fazovoi ploskosti (ris. 2.7b) fazovaya traektoriya budet postepenno "raskruchivat'sya" iz nachala koordinat i stremit'sya k predel'nomu ciklu - ellipsu, izobrazhennomu na risunke punktirnoi liniei.

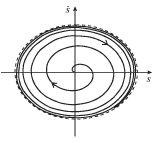Ris. 2.7b.

Harakteristiki razlichnyh kolebatel'nyh sistem (oscillyatorov).

Interesno sopostavit' osnovnye harakteristiki razlichnyh kolebatel'nyh sistem (inogda ih dlya kratkosti nazyvayut oscillyatorami) Primerami takih oscillyatorov mogut byt' mehanicheskie (rassmotrennye vyshe), elektricheskie (izvestnye iz shkol'nogo kursa fiziki, naprimer, kolebatel'nyi kontur), opticheskie (naprimer, elektron v atome) i drugie sistemy.

Vnachale obratimsya k harakteristikam naibolee rasprostranennogo oscillyatora - mayatnika, predstavlyayushego soboi telo, podveshennoe na niti.

Mayatnik yavlyaetsya odnim iz drevneishih fizicheskih priborov. S pomosh'yu krutil'nyh mayatnikov byli otkryty zakony gravitacionnogo i elektricheskogo vzaimodeistvii, izmereno davlenie sveta, vypolneno mnozhestvo drugih fizicheskih eksperimentov. V poslednee vremya predlozhen i realizuetsya ryad novyh eksperimentov dlya izucheniya fundamental'nyh svoistv materii, v kotoryh ochen' malye sily izmeryayutsya s pomosh'yu krutil'nyh mayatnikov. Chuvstvitel'nost' takih eksperimentov zavisit ot togo, naskol'ko oslableny seismicheskie vozmusheniya, deistvuyushie na mayatnik, a takzhe ot stabil'nosti ego parametrov, naprimer, uprugih svoistv niti podvesa. No dazhe esli ustraneny vse vneshnie vozmushayushie vozdeistviya, ostaetsya odin principial'nyi istochnik fluktuacii ego amplitudy i fazy kolebanii. Eto haoticheskoe teplovoe dvizhenie molekul v niti podvesa i podveshennom tele. Deistvuyushaya na nego fluktuacionnaya sila zavisit ot temperatury i ot dobrotnosti mayatnika. Chem vyshe dobrotnost' mayatnika, tem medlennee zatuhayut ego kolebaniya i dissipiruet ego energiya, prevrashayas' v teplo, t.e. haoticheskoe dvizhenie molekul. Eto oznachaet, chto oslabevaet i obratnyi process raskachki mayatnika haoticheskim dvizheniem molekul, t.e. umen'shaetsya fluktuacionnaya sila, deistvuyushaya na mayatnik. Dlya togo, chtoby umen'shit' zatuhanie, telo i nit' podvesa izgotovlyayut iz vysokokachestvennogo plavlenogo kvarca - materiala s nizkimi poteryami uprugoi energii, a takzhe prinimayut special'nye mery dlya isklyucheniya drugih istochnikov dissipacii energii. V rezul'tate dobrotnost' krutil'nyh mayatnikov dostigaet velichiny ~10⁷.

V nastoyashee vremya v neskol'kih stranah stroyatsya lazernye gravitacionnye antenny dlya registracii gravitacionnogo izlucheniya ot kosmicheskih ob'ektov. Princip deistviya antenny osnovan na tom, chto gravitacionnaya volna deistvuet na svobodnye massy, pomeshennye v raznye tochki prostranstva, izmenyaya rasstoyanie mezhdu nimi. Eto izmenenie proporcional'no intensivnosti volny i rasstoyaniyu mezhdu massami. Po etoi prichine v gravitacionnyh antennah probnye massy raspolagayut v neskol'kih kilometrah drug ot druga v special'nyh vakuumnyh kamerah, a rasstoyanie mezhdu nimi izmeryayut unikal'nym lazernym interferometrom. Kazhdaya probnaya massa podveshivaetsya na tonkih nityah, obrazuya mayatnik kachaniya. S massami svyazyvayut dva zerkala, otrazhayushie lazernyi luch, rasprostranyayushiisya vdol' pryamoi, soedinyayushei eti massy. Po sdvigu interferencionnoi kartiny, davaemoi takoi slozhnoi opticheskoi sistemoi, mozhno "pochuvstvovat'" vzaimnoe smeshenie mass na velichinu poryadka 10^-17 sm, chto na 7 poryadkov men'she razmerov atoma! Chuvstvitel'nost' gravitacionnoi antenny ogranichena teplovymi fluktuaciyami kolebanii takogo mayatnika, a znachit, takzhe opredelyaetsya ego dobrotnost'yu. V otlichie ot krutil'nyh, dobrotnost' mayatnikov kachaniya zavisit ne tol'ko ot poter' v uprugom elemente - niti podvesa, no i ot ee natyazheniya. Za schet etogo effekta mozhno znachitel'no uvelichit' dobrotnost' mayatnika kachaniya. Tak, dobrotnost' mayatnikov kachaniya, celikom izgotovlennyh iz plavlenogo kvarca, mozhet prevyshat' 10⁸, t.e. vremya zatuhaniya ih kolebanii dostigaet neskol'kih let. Konechno, pri stol' maloi dissipacii energii mayatnika na ego dobrotnost' vliyayut ves'ma slabye vneshnie vozdeistviya, naprimer, elektricheskie i magnitnye polya, ili chasticy pyli, osevshie na niti podvesa, i t. d.

Pri takih vysokih znacheniyah dobrotnosti i sootvetstvuyushem podavlenii seismicheskih vozmushenii proyavlyayutsya kvantovye svoistva mayatnika. V etom sluchae povedenie vpolne makroskopicheskogo ob'ekta budet opredelyat'sya principom neopredelennosti Geizenberga. Pravda, neobhodimye usloviya realizuyutsya poka dlya malyh vremennyh intervalov (okolo 10^-3 s), i dlya nablyudeniya kvantovyh osobennostei povedeniya mayatnikov trebuyutsya ochen' chuvstvitel'nye registriruyushie ustroistva, no imenno takie mayatniki, obladayushie predel'no vysokoi dobrotnost'yu, predpolagaetsya ispol'zovat' v budushih gravitacionnyh antennah.

Kamerton, sluzhashii dlya nastroiki muzykal'nyh instrumentov, takzhe yavlyaetsya vysokodobrotnym oscillyatorom. Zvuk, izdavaemyi vibriruyushimi nozhkami kamertona, zatihaet za dostatochno dlitel'noe vremya po sravneniyu s periodom ih kolebanii. Esli, naprimer, sobstvennaya chastota kamertona lezhit v diapazone $\nu = 300\div 400 Gc,$ a prodolzhitel'nost' zvuchaniya (ves'ma grubo) sostavlyaet vremya poryadka $\tau \sim 10 s,$ to kamerton sovershit $\nu \tau \sim 3000\div 4000$ kolebanii. Eto oznachaet, chto ego dobrotnost' po poryadku velichiny ravna $Q\sim 10^{4}.$

Kak eto ni pokazhetsya paradoksal'nym, elektricheskii kolebatel'nyi kontur yavlyaetsya menee dobrotnoi sistemoi, hotya chastota ego sobstvennyh kolebanii imeet poryadok velichiny $\nu \sim (10^{5}\div 10^{8}) Gc.$ Dobrotnost' kontura ogranichena, glavnym obrazom, omicheskimi poteryami i imeet poryadok velichiny $Q\sim 10^{2}.$ Eto, v svoyu ochered', oznachaet, chto polosa propuskaniya $\Delta \nu = Q^{ - 1} \cdot \nu ,$ vvedennaya ranee pri rassmotrenii vynuzhdennyh kolebanii, ravna $\Delta \nu \sim (10^{3}\div 10^{6}) Gc.$

Esli chastota radioperedayushei stancii $\nu _{c}$ vysoka $(\nu _{c} \gt 10^{6} Gc),$ to ee preobrazovyvayut v radiopriemnyh ustroistvah do nizkoi (nazyvaemoi promezhutochnoi) chastoty $\nu _{p} \sim 10^{5} Gc.$ Togda kolebatel'nyi kontur radiopriemnika budet imet' ochen' maluyu polosu propuskaniya $\Delta \nu \sim Q \cdot \nu _{p} \sim 5 \cdot 10^{3} Gc.$ Eto znachit, chto esli chastoty dvuh stancii $\nu _{1c}$ i $\nu _{2c}$ sootvetstvenno razlichayutsya bolee, chem na velichinu polosy propuskaniya $({\displaystyle \left| {\displaystyle \nu _{1c} - \nu _{2c} } \right|} \gt \Delta \nu ),$ to, perestraivaya sobstvennuyu chastotu kolebatel'nogo kontura priemnika, mozhno po otdel'nosti nastroit'sya na kazhduyu iz etih peredayushih stancii.

Opticheskii elektron v atome, osushestvlyaya perehody s odnoi orbity na druguyu, v sootvetstvii s postulatami Bora izluchaet kvant sveta s energiei $\hbar \omega = E_{2} - E_{1} .$ S klassicheskoi tochki zreniya eto mozhno interpretirovat' takim obrazom, chto elektron sovershaet kolebaniya na etoi chastote $\omega ,$ t.e. yavlyaetsya opticheskim oscillyatorom. Poskol'ku elektron teryaet energiyu na izluchenie, to amplituda ego kolebanii dolzhna zatuhat' v techenie nekotorogo harakternogo vremeni $\tau .$ Dlya uedinennogo atoma (ne vzaimodeistvuyushego s sosednimi atomami) eto vremya opredelyaetsya zaryadom i massoi elektrona i zavisit ot chastoty $\omega .$ Odnako dlya vseh atomov ono imeet odin i tot zhe poryadok velichiny: $\tau \sim 10^{ - 8}\div 10^{ - 9}c.$ Uchityvaya, chto v vidimom opticheskom diapazone period kolebanii $T = {\displaystyle {\displaystyle 2\pi } / {\displaystyle \omega }}\sim 10^{ - 15}c,$ legko podschitat' chislo kolebanii do ih zatuhaniya. Ono imeet poryadok velichiny ${\displaystyle \frac{\displaystyle {\displaystyle \tau }}{\displaystyle {\displaystyle T}}}\sim 10^{6}\div 10^{7}.$ Poetomu dobrotnost' opticheskogo oscillyatora $(Q\sim 10^{7}),$ buduchi vysokoi, vse zhe ustupaet dobrotnosti precizionnyh kvarcevyh mayatnikov.

Nazad| Vpered

Publikacii s klyuchevymi slovami: kolebaniya - volny Publikacii so slovami: kolebaniya - volny
Sm. takzhe: Eho iz glubin krasnogo giganta

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce