Astronet > Kolebaniya i volny

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Kolebaniya i volny. Lekcii.

V.A.Aleshkevich, L.G.Dedenko, V.A.Karavaev (Fizicheskii fakul'tet MGU)
Izdatel'stvo Fizicheskogo fakul'teta MGU, 2001 g. Soderzhanie

V povsednevnoi zhizni my stalkivaemsya s nezatuhayushimi kolebaniyami, dlya podderzhaniya kotoryh trebuetsya periodicheski menyat' kakoi-libo parametr kolebatel'noi sistemy. Odnim iz yarkih primerov yavlyayutsya kolebaniya kachelei. Horosho izvestno, chto mozhno podderzhivat' kolebaniya dlitel'noe vremya, esli bystro prisedat' v moment naibol'shego otkloneniya kachelei i takzhe bystro vstavat' pri prohozhdenii polozheniya ravnovesiya. Blagodarya etomu parametr fizicheskogo mayatnika (kachelei) - rasstoyanie $a$ mezhdu os'yu vrasheniya i centrom mass - menyaetsya skachkoobrazno na velichinu $\pm \Delta a (\Delta a \ll a)$ .Velichina $\Delta a$ dolzhna byt' takoi, chtoby obespechit' balans energii sistemy: poteri energii mayatnika za period dolzhny kompensirovat'sya za schet soversheniya raboty, osushestvlyaemoi pri prisedanii i vstavanii.

Napishem uslovie energeticheskogo balansa dlya prosteishego sluchaya kolebanii matematicheskogo mayatnika s dlinoi niti a, kotoraya menyaetsya na velichinu $\pm \Delta a$ (ris. 2.8.). Eto mozhno osushestvit', esli propustit' nit' mayatnika cherez otverstie v tochke P (tochke podvesa) i zatem, prikladyvaya vneshnyuyu silu $\bf F$ k koncu niti, periodicheski menyat' ee dlinu.

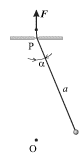Ris.2.8.

Rassmotrim ustanovivshiesya parametricheskie kolebaniya mayatnika s ne slishkom bol'shimi amplitudami i budem schitat', chto zatuhanie malo $(\delta \ll \omega _{0} ).$ Poskol'ku $\Delta a \ll a,$ to priblizhenno mozhno schitat', chto ugol $\alpha$ otkloneniya mayatnika ot polozheniya ravnovesiya menyaetsya vo vremeni po garmonicheskomu zakonu

$\alpha (t) = \alpha _{0} \sin \omega t,$

(2.53)

gde soglasno (1.42) 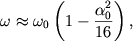$\omega \approx \omega _{0} \left( {\displaystyle 1 - {\displaystyle \frac{\displaystyle {\displaystyle \alpha _{0}^{2} }}{\displaystyle {\displaystyle 16}}}} \right),$ a $\omega _{0} = \sqrt {\displaystyle {\displaystyle {\displaystyle g} / {\displaystyle a}}.}$

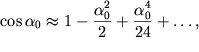V moment naibol'shego otkloneniya na ugol $\alpha _{0}$ sila natyazheniya niti ravna $N_{1} = mg\cos \alpha _{0} .$ Poetomu, udlinyaya nit' na velichinu $\Delta a,$ vneshnyaya sila $F_{1} = N_{1}$ sovershaet otricatel'nuyu rabotu $A_{ - } = - mg\cos \alpha _{0} \cdot \Delta a.$ Raskladyvaya $\cos \alpha _{0}$ v ryad $\cos \alpha _{0} \approx 1 - {\displaystyle \frac{\displaystyle {\displaystyle \alpha _{0}^{2} }}{\displaystyle {\displaystyle 2}}} + {\displaystyle \frac{\displaystyle {\displaystyle \alpha _{0}^{4} }}{\displaystyle {\displaystyle 24}}} + \ldots,$ poluchim

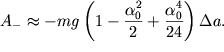$A_{ - } \approx - mg\left( {\displaystyle 1 - {\displaystyle \frac{\displaystyle {\displaystyle \alpha _{0}^{2} }}{\displaystyle {\displaystyle 2}}} + {\displaystyle \frac{\displaystyle {\displaystyle \alpha _{0}^{4} }}{\displaystyle {\displaystyle 24}}}} \right)\Delta a.$

(2.54)

Pri prohozhdenii mayatnikom polozheniya ravnovesiya 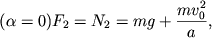$(\alpha = 0) F_{2} = N_{2} = mg + {\displaystyle \frac{\displaystyle {\displaystyle mv_{0}^{2} }}{\displaystyle {\displaystyle a}}},$ gde $v_{0} = \alpha _{0} \omega a.$ Poetomu polozhitel'naya rabota pri ukorachivanii niti s tochnost'yu do chlenov poryadka $\alpha _{0}^{4}$ ravna:

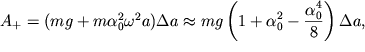$A_{ + } = (mg + m\alpha _{0}^{2} \omega ^{2}a)\Delta a \approx mg\left( {\displaystyle 1 + \alpha _{0}^{2} - {\displaystyle \frac{\displaystyle {\displaystyle \alpha _{0}^{4} }}{\displaystyle {\displaystyle 8}}}} \right)\Delta a,$

(2.55)

gde uchteno, chto $\omega _{0}^{2} a = g.$

Polnaya rabota, sovershaemaya za period vneshnei siloi ${\displaystyle \bf F},$ budet polozhitel'noi i ravnoi

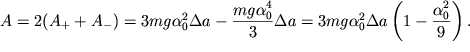$A = 2(A_{ + } + A_{ - } ) = 3mg\alpha _{0}^{2} \Delta a - {\displaystyle \frac{\displaystyle {\displaystyle mg\alpha _{0}^{4} }}{\displaystyle {\displaystyle 3}}}\Delta a = 3mg\alpha _{0}^{2} \Delta a\left( {\displaystyle 1 - {\displaystyle \frac{\displaystyle {\displaystyle \alpha _{0}^{2} }}{\displaystyle {\displaystyle 9}}}} \right).$

(2.56)

Poteri energii za period chislenno ravny rabote sily treniya:

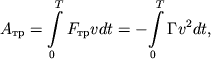$A_{tr} = {\displaystyle \int\limits_{0}^{T} {\displaystyle F_{tr} vdt = - {\displaystyle \int\limits_{0}^{T} {\displaystyle \Gamma v^{2}dt,} }} }$

(2.57)

gde $F_{tr} = - \Gamma v.$

Pri garmonicheskih kolebaniyah (2.53) skorost'

$v(t) = a\dot {\displaystyle \alpha }(t) = a\alpha _{0} \omega \cos \omega t.$

(2.58)

Podstavlyaya (2.58) v (2.57) i vypolnyaya integrirovanie, poluchaem:

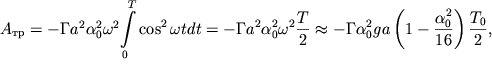$A_{tr} = - \Gamma a^{2}\alpha _{0}^{2} \omega ^{2}{\displaystyle \int\limits_{0}^{T} {\displaystyle \cos ^{2}\omega tdt = - \Gamma a^{2}\alpha _{0}^{2} \omega ^{2}{\displaystyle \frac{\displaystyle {\displaystyle T}}{\displaystyle {\displaystyle 2}}} \approx - \Gamma \alpha _{0}^{2} ga\left( {\displaystyle 1 - {\displaystyle \frac{\displaystyle {\displaystyle \alpha _{0}^{2} }}{\displaystyle {\displaystyle 16}}}} \right){\displaystyle \frac{\displaystyle {\displaystyle T_{0} }}{\displaystyle {\displaystyle 2}}}} },$

(2.59)

poskol'ku $\omega T = \omega _{0} T_{0} = 2\pi .$

Sledovatel'no, uslovie balansa energii sostoit v ravenstve nulyu summy rabot: $A + A_{tr} = 0,$ ili

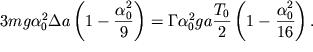$3mg\alpha _{0}^{2} \Delta a\left( {\displaystyle 1 - {\displaystyle \frac{\displaystyle {\displaystyle \alpha _{0}^{2} }}{\displaystyle {\displaystyle 9}}}} \right) = \Gamma \alpha _{0}^{2} ga{\displaystyle \frac{\displaystyle {\displaystyle T_{0} }}{\displaystyle {\displaystyle 2}}}\left( {\displaystyle 1 - {\displaystyle \frac{\displaystyle {\displaystyle \alpha _{0}^{2} }}{\displaystyle {\displaystyle 16}}}} \right).$

(2.60)

Provodya sokrasheniya i ispol'zuya opredelenie vyrazhenie dlya dobrotnosti $Q \approx {\displaystyle \frac{\displaystyle {\displaystyle \pi }}{\displaystyle {\displaystyle \delta T_{0} }}},$ poluchaem priblizhennoe vyrazhenie dlya amplitudy $\alpha _{0}$ ustanovivshihsya parametricheskih kolebanii:

$\alpha _{0} = {\displaystyle \frac{\displaystyle {\displaystyle 12}}{\displaystyle {\displaystyle \sqrt {\displaystyle 7} }}}\sqrt {\displaystyle 1 - {\displaystyle \frac{\displaystyle {\displaystyle \pi }}{\displaystyle {\displaystyle 3Q(\Delta {\displaystyle {\displaystyle a} / {\displaystyle a}})}}}} .$

(2.61)

Otnoshenie $\Delta a / a$ nazyvayut glubinoi modulyacii parametra $a.$ Iz (2.61) vidno, chto dlya vozniknoveniya parametricheskih kolebanii glubina modulyacii dolzhna prevzoiti nekotoroe minimal'noe (porogovoe) znachenie, primerno ravnoe velichine, obratnoi dobrotnosti:

${\displaystyle \frac{\displaystyle {\displaystyle \Delta a}}{\displaystyle {\displaystyle a}}} \geq {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle Q}}}.$

(2.62)

Chem bolee dobrotna sistema, tem men'she porogovaya glubina modulyacii. S povysheniem velichiny $\Delta a / a$ amplituda kolebanii $\alpha _{0} ,$ kak eto sleduet iz formuly (2.61), budet uvelichivat'sya. Odnako pri bol'shih amplitudah $(\alpha _{0} \gt 1)$ formula (2.61) stanovitsya malo priemlemoi, poskol'ku sdelannye nami priblizheniya stanovyatsya neprimenimymi.

Sleduet otmetit', chto parametricheskoe vozbuzhdenie yavlyaetsya sushestvenno nelineinym effektom. Eto vidno, v chastnosti, iz uravneniya (2.60): esli prenebrech' v nem malymi slagaemymi $\sim \alpha _{0}^{2} ,$ kotorye opisyvayut nelineinost', to $\alpha _{0}$ iz uravneniya vypadaet, i poluchaetsya sootnoshenie ${\displaystyle \frac{\displaystyle {\displaystyle \Delta a}}{\displaystyle {\displaystyle a}}} = {\displaystyle \frac{\displaystyle {\displaystyle \pi }}{\displaystyle {\displaystyle 3Q}}}.$ Fizicheski eto oznachaet, chto pri etom znachenii glubiny modulyacii energeticheskii balans v sisteme obespechivaetsya pri lyubyh amplitudah $\alpha _{0} ,$ chto neverno.

Zametim, chto vozbuzhdenie parametricheskih kolebanii, voobshe govorya, mozhet proishodit' ne tol'ko na udvoennoi chastote sobstvennyh kolebanii sistemy, kogda parametr menyaetsya odin raz za kazhdye polperioda, no i pri bolee redkom vozdeistvii: cherez odin, dva, tri i t. d. polperiodov kolebanii, t.e. na chastotah $2\omega _{0} / n,$ gde $n$ - lyuboe celoe chislo. Vozbuzhdenie takzhe vozmozhno vnutri nekotoroi oblasti - vblizi kazhdoi iz etih chastot, no porogovye znacheniya glubiny modulyacii dlya raznyh chastot budut razlichny.

Avtokolebaniya.

Nablyudaya kolebaniya list'ev derev'ev, dorozhnyh znakov nad proezzhei chast'yu ulic, polotnish na vetru i dr., my ponimaem, chto vo vseh perechislennyh sluchayah nezatuhayushie kolebaniya proishodyat za schet energii postoyanno duyushego vetra. Pri etom sama kolebatel'naya sistema proizvodit otbor energii vetra v nuzhnyi moment vremeni i v kolichestve, trebuemom dlya kompensacii neizbezhno prisutstvuyushih energeticheskih poter'. Kolebaniya v etih sistemah nachinayutsya samoproizvol'no za schet nachal'nyh fluktuacii (drozhanii) koleblyushihsya predmetov. Chastota i amplituda ustanovivshihsya kolebanii opredelyaetsya kak parametrami samoi sistemy, tak i parametrami ee vzaimodeistviya s vetrom. Takie kolebaniya yavlyayutsya primerami avtokolebanii, a sami sistemy - primerami avtokolebatel'nyh sistem.

Klassicheskim primerom avtokolebatel'noi sistemy sluzhat mehanicheskie chasy s mayatnikom i giryami. Eti chasy periodicheski "cherpayut" energiyu pri opuskanii gir', podveshennyh k cepochke, perekinutoi cherez shesternyu chasovogo mehanizma.

Princip raboty vseh avtokolebatel'nyh sistem mozhno ponyat', obrativshis' k sheme, izobrazhennoi na ris. 2.9a.

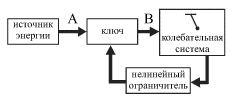Ris. 2.9a.

Periodicheskim postupleniem energii v kolebatel'nuyu sistemu ot istochnika energii po kanalu AV upravlyaet sama kolebatel'naya sistema posredstvom obratnoi svyazi. Shematicheski eto izobrazheno v vide nekotorogo zapirayushego kanal AV ustroistva (klyucha), kotoryi upravlyaetsya samoi sistemoi. Tak, v zavisimosti ot polozheniya i skorosti koleblyushegosya lista na vetru budet razlichnoi moshnost' sil aerodinamicheskogo davleniya. V konstrukcii chasovogo mehanizma (ris. 2.9b) prisutstvuet special'noe ustroistvo - anker, vypolnyayushii rol' klyucha. Etot anker, predstavlyayushii soboi koromyslo, privoditsya v kolebanie samim mayatnikom chasov. Pri opredelennyh polozheniyah on "otpiraet" odnu iz shesteren chasovogo mehanizma. V etot moment vremeni shesternya provorachivaetsya za schet momenta sil, prilozhennogo so storony natyanutoi cepi s gruzom. Gruz pri etom opuskaetsya na nebol'shuyu velichinu. Kolichestvo energii, postupayushei v chasovoi mehanizm, ravno po velichine umen'sheniyu potencial'noi energii gruza v pole sily tyazhesti.

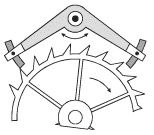Ris. 2.9b.

Vazhno otmetit', chto lyubaya avtokolebatel'naya sistema nelineina. Na sheme eto otrazheno nalichiem v sisteme obratnoi svyazi nelineinogo ogranichitelya signala, upravlyayushego klyuchom. Nelineinost' sistemy proyavlyaetsya v tom, chto pri nachal'nom narastanii amplitudy kolebanii, porozhdennyh fluktuaciyami, postuplenie energii v sistemu za kazhdyi posleduyushii period kolebanii uvelichivaetsya nelineino, t.e. prirost postupayushei energii stanovitsya vse men'she i men'she. Estestvenno, chto amplituda kolebanii dostignet takoi ustanovivsheisya velichiny, pri kotoroi pritok energii i ee poteri budut ravny po velichine.

Nazad| Vpered

Publikacii s klyuchevymi slovami: kolebaniya - volny Publikacii so slovami: kolebaniya - volny
Sm. takzhe: Eho iz glubin krasnogo giganta

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

Kolebaniya i volny. Lekcii.

Parametricheskie kolebaniya.

Avtokolebaniya.