Astronet > Kolebaniya i volny

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Kolebaniya i volny. Lekcii.

V.A.Aleshkevich, L.G.Dedenko, V.A.Karavaev (Fizicheskii fakul'tet MGU)
Izdatel'stvo Fizicheskogo fakul'teta MGU, 2001 g. Soderzhanie

Mayatnik na vrashayushemsya valu (mayatnik Fruda).

Dlya bolee uglublennogo izucheniya principa deistviya avtokolebatel'noi sistemy proanaliziruem kolebaniya mayatnika, podves kotorogo skreplen s muftoi 1, odetoi na gorizontal'nyi val 2 (ris. 2.10).

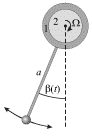Ris. 2.10.

Pust' val vrashaetsya s postoyannoi uglovoi skorost'yu $\Omega$ po chasovoi strelke. Esli ugol otkloneniya mayatnika ot vertikali $\beta (t)$ menyaetsya s techeniem vremeni, to sila suhogo treniya v podvese, nelineino zavisyashaya ot otnositel'noi skorosti mufty i vala $\Omega - \dot {\displaystyle \beta },$ takzhe budet menyat'sya vo vremeni ( $\dot {\displaystyle \beta }$ - uglovaya skorost' mufty). Moment etoi sily $M_{tr}$ budet okazyvat' periodicheskoe vozdeistvie na mayatnik, podderzhivaya ego kolebaniya. Na ris. 2.11 izobrazhena nelineinaya zavisimost' $M_{tr}$ ot otnositel'noi uglovoi skorosti mufty i vala. Na izobrazhennoi krivoi imeetsya tochka peregiba P. Podberem skorost' vrasheniya vala $\Omega$ takoi, chtoby v otsutstvie kolebanii $(\dot {\displaystyle \beta } = 0)$ popast' v etu tochku. V etom sluchae k mufte mayatnika budet prilozhen postoyannyi moment sily treniya: $M_{tr} = M_{0} .$ Dlya dal'neishego analiza bolee udobno vospol'zovat'sya zavisimost'yu $M_{tr} (\dot {\displaystyle \beta }),$ izobrazhennoi na ris. 2.12. Sleduet podcherknut', chto nachal'noe (lineinoe) narastanie $M_{tr}$ s uglovoi skorost'yu $\dot {\displaystyle \beta }$ obespechivaet uslovie dlya samoproizvol'nogo narastaniya kolebanii iz fluktuacii, chto ekvivalentno nalichiyu polozhitel'noi obratnoi svyazi, a posleduyushee zamedlenie rosta $M_{tr}$ pri uvelichenii $\dot {\displaystyle \beta }$ yavlyaetsya prichinoi nelineinogo ogranicheniya narastaniya kolebanii: amplituda smesheniya mayatnika (a znachit i amplituda ego skorosti $\dot {\displaystyle \beta }_{\max } )$ dostignet maksimal'noi (ustanovivsheisya) velichiny, chto ekvivalentno nalichiyu nelineinogo ogranichitelya.


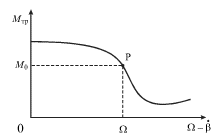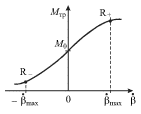Ris. 2.11.	Ris. 2.12.

Otklonim ostorozhno mayatnik ot vertikali na ugol $\beta _{0}$ takoi, chtoby moment sily treniya, deistvuyushii na nepodvizhnyi mayatnik, $M _{0} = M_{tr} (0),$ byl uravnoveshen momentom sily tyazhesti $M(\beta _{0} ) = mga\sin \beta _{0}$ :

$M_{tr} (0) = M(\beta _{0} ),ili \quad M_{0} = mga\sin \beta _{0} .$

(2.63)

Zdes' $m$ - massa mayatnika, $a$ - rasstoyanie ot vala do centra mass mayatnika.

Na pervyi vzglyad, mozhet pokazat'sya, chto mayatnik tak i ostanetsya viset' pod uglom $\beta _{0}$ k vertikali. Na samom dele eto polozhenie budet neustoichivym. Predstavim, chto v rezul'tate nichtozhnogo tolchka mayatnik priobretet nebol'shuyu uglovuyu skorost' $\dot {\displaystyle \beta } \gt 0.$ Pri etom vozrastut momenty sil tyazhesti $M$ i treniya $M_{tr},$ i uslovie (2.63) mozhet narushit'sya. Esli nachal'nyi naklon krivoi $M_{tr}(\dot {\displaystyle \beta })$ na ris. 2.12 dostatochno velik (sil'naya polozhitel'naya obratnaya svyaz'), to $M_{tr} (\dot {\displaystyle \beta }) \gt M(\beta _{0} ).$ Eto oznachaet, chto uglovaya skorost' $\dot {\displaystyle \beta }$ budet narastat'. Odnako zatem eto narastanie prekratitsya, t.k. iz-za nelineinogo zagiba krivoi $M_{tr}(\dot {\displaystyle \beta })$ ravenstvo momentov opyat' vosstanovitsya (srabotaet mehanizm nelineinogo ogranicheniya):

$M_{tr} (\dot {\displaystyle \beta }_{\max } ) = M(\beta ).$

(2.64)

Usloviyu (2.64) sootvetstvuet tochka $R_{ + }$ na krivoi $M_{tr}(\dot {\displaystyle \beta }).$ Posle etogo uglovaya skorost' nachnet umen'shat'sya, poskol'ku s rostom ugla $\beta$ moment $M(\beta )$ prodolzhaet rasti, a $M_{tr}(\dot {\displaystyle \beta })$ - ubyvat'. Sledovatel'no, mayatnik spustya kakoe-to vremya ostanovitsya, a ego ugol otkloneniya dostignet maksimal'noi velichiny $\beta _{\max } .$ Poskol'ku v etot moment $M(\beta _{\max } ) \gt M_{tr} = M_{0} ,$ to mayatnik nachnet dvigat'sya v obratnom napravlenii. Moment sily tyazhesti nachnet umen'shat'sya, a moment sily treniya budet takzhe umen'shat'sya, no bystree, chem moment sily tyazhesti (opyat' srabatyvaet polozhitel'naya obratnaya svyaz'). Snachala eto dvizhenie budet uskorennym, poka $M \gt M_{tr}$ (do tochki R_- na ris. 2.12), a zatem pri $M \lt M_{tr}$ - zamedlennym (do tochki P na ris. 2.12). Ostanovivshis' pri nekotorom ugle naklona $\beta _{\min } ,$ mayatnik opyat' dvizhetsya vlevo, t.k. vse eshe $M \lt M_{tr} .$ Nakonec, on dostigaet startovoi pozicii, odnako priobretennaya im skorost' budet bol'she skorosti nachal'nogo tolchka. Takim obrazom, v techenie odnogo perioda kolebanii uvelichilas' energiya mayatnika za schet ee zaimstvovaniya ot ustroistva, vrashayushego val.

V posleduyushie periody kolebanii tochki R₊ i R $-$ na krivoi $M_{tr} (\dot {\displaystyle \beta })$ budut sdvigat'sya v raznye storony, odnako iz-za nelineinosti krivoi etot sdvig prekratitsya (srabatyvaet mehanizm nelineinogo ogranicheniya), i kolebaniya ustanovyatsya.

Chtoby kolichestvenno proanalizirovat' avtokolebaniya mayatnika, zapishem uravnenie vrashatel'nogo dvizheniya mayatnika s momentom inercii $J$ :

$J\ddot {\displaystyle \beta } = M_{tr} (\dot {\displaystyle \beta }) - mga\sin \beta .$

(2.65)

V etom uravnenii my poka prenebrezhem momentom sily vyazkogo treniya, deistvuyushei na dvizhushiisya mayatnik. Moment sily suhogo treniya v podvese, nelineino zavisyashii ot uglovoi skorosti $\dot {\displaystyle \beta }$ (sm. ris. 2.12), mozhno approksimirovat' sleduyushim vyrazheniem

$M_{tr} (\dot {\displaystyle \beta }) = M_{0} + k_{1} \dot {\displaystyle \beta } - k_{2} \dot {\displaystyle \beta }^{3},$

(2.66)

gde $k_{1}$ i $k_{2}$ - razmernye koefficienty, opredelyayushie obratnuyu svyaz' i nelineinoe ogranichenie sootvetstvenno. Esli kolebanie opisyvat' uglom otkloneniya $\alpha$ ot polozheniya neustoichivogo ravnovesiya, zadavaemogo uglom $\beta _{0} (\alpha = \beta - \beta _{0} ),$ to

$mga\sin \beta = mga(\sin \beta _{0} \cos \alpha + \cos \beta _{0} \sin \alpha ).$

(2.67)

Dlya malyh uglov $\alpha \cos \alpha \approx 1, \sin \alpha \approx \alpha .$ Esli uchest' dalee, chto $\dot {\displaystyle \beta } = \dot {\displaystyle \alpha },$ to uravnenie (2.65) primet vid:

$J\ddot {\displaystyle \alpha } + mga\cos \beta _{0} \alpha = k_{1} \dot {\displaystyle \alpha } - k_{2} \dot {\displaystyle \alpha }^{3}.$

(2.68)

Eto uravnenie yavlyaetsya nelineinym differencial'nym uravneniem i ne imeet analiticheskogo resheniya. V teorii kolebanii razvity metody, pozvolyayushie reshit' ego priblizhenno, issledovat' usloviya, pri kotoryh vozmozhno samovozbuzhdenie kolebanii, i naiti amplitudu $\alpha _{0}$ i chastotu $\omega$ ustanovivshihsya kolebanii:

$\alpha (t) = \alpha _{0} \sin \omega t.$

(2.69)

My zhe postupim bolee prosto i opredelim $\alpha _{0}$ iz usloviya energeticheskogo balansa. Poskol'ku pravaya chast' (2.68) mala, to chastota kolebanii priblizhenno ravna: $\omega = \sqrt {\displaystyle {\displaystyle {\displaystyle mga\cos \beta _{0} } / {\displaystyle J}}} .$

Podschitaem rabotu za period kolebanii $T = {\displaystyle {\displaystyle 2\pi } / {\displaystyle \omega ,}}$ sovershaemuyu ustroistvom (naprimer, elektrodvigatelem), vrashayushim val. Ona, ochevidno, ravna:

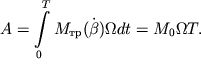$A = {\displaystyle \int\limits_{0}^{T} {\displaystyle M_{tr} (\dot {\displaystyle \beta })\Omega dt = M_{0} \Omega T.} }$

(2.70)

Zdes' uchteno, chto integraly po vremeni ot $\dot {\displaystyle \beta }$ i $\dot {\displaystyle \beta }^{3}$ ravny nulyu, poskol'ku

$\dot {\displaystyle \beta } = \dot {\displaystyle \alpha } = \alpha _{0} \omega \cos \omega t.$

(2.71)

Poteri energii v skol'zyashem podvese za eto vremya sostavyat velichinu

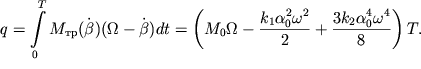$q = {\displaystyle \int\limits_{0}^{T} {\displaystyle M_{tr} (\dot {\displaystyle \beta })(\Omega - \dot {\displaystyle \beta })dt} } = \left( {\displaystyle M_{0} \Omega - {\displaystyle \frac{\displaystyle {\displaystyle k_{1} \alpha _{0}^{2} \omega ^{2}}}{\displaystyle {\displaystyle 2}}} + {\displaystyle \frac{\displaystyle {\displaystyle 3k_{2} \alpha _{0}^{4} \omega ^{4}}}{\displaystyle {\displaystyle 8}}}} \right)T.$

(2.72)

Na ris. 2.13 izobrazheny zavisimosti $A$ i $q$ ot amplitudy $\alpha _{0} .$ Vidno, chto pri sluchainyh fluktuaciyah, kogda $\alpha _{0}$ malo, $A \gt q.$ Eto oznachaet, chto kolebaniya budut narastat'. Odnako s rostom amplitudy nachinayut rasti poteri $q$ . Kolebaniya ustanovyatsya pri $A = q$ (tochka R na grafike). Amplituda ustanovivshihsya kolebanii opredelitsya iz ravenstva

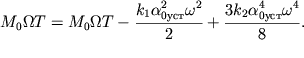$M_{0} \Omega T = M_{0} \Omega T - {\displaystyle \frac{\displaystyle {\displaystyle k_{1} \alpha _{0ust}^{2} \omega ^{2}}}{\displaystyle {\displaystyle 2}}} + {\displaystyle \frac{\displaystyle {\displaystyle 3k_{2} \alpha _{0ust}^{4} \omega ^{4}}}{\displaystyle {\displaystyle 8}}}.$

(2.73)

Otsyuda

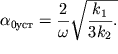$\alpha _{0ust} = {\displaystyle \frac{\displaystyle {\displaystyle 2}}{\displaystyle {\displaystyle \omega }}}\sqrt {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle k_{1} }}{\displaystyle {\displaystyle 3k_{2} }}}.}$

(2.74)

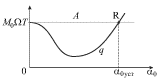Ris. 2.13.

Zametim, chto teper' my mozhem legko uchest' sily vyazkogo treniya, dlya chego v pravuyu chast' uravneniya (2.68) sleduet dobavit' chlen - $\Gamma \dot {\displaystyle \alpha }.$ Eto privedet k tomu, chto $k_{1}$ v (2.74) budet umen'shen na velichinu $\Gamma .$ Poetomu (2.74) izmenitsya:

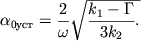(2.)

Iz poslednego vyrazheniya sleduet, chto pri $\Gamma \ge k_{1}$ kolebaniya ne mogut samoproizvol'no nachat'sya.

Avtokolebatel'nye sistemy nahodyat shirochaishee primenenie v tehnike. Tak, naprimer, duhovye i smychkovye instrumenty, organnye truby, generatory elektromagnitnogo izlucheniya v priemno-peredayushih liniyah svyazi, opticheskie kvantovye generatory (lazery) i dr. predstavlyayut primery avtokolebatel'nyh sistem.

Odnako, avtokolebaniya mogut igrat' i negativnuyu rol', nachinaya ot bezobidnyh kolebanii detalei kranov vodoprovodnyh sistem, "revushih" pri dostatochnom napore vody, do opasnyh kolebanii kryl'ev samoletov, poluchivshih nazvanie "flatter". V noyabre 1940 g. podvesnoi most cherez reku Takoma v SShA razrushilsya iz-za krutil'nyh avtokolebanii, voznikshih pod deistviem duvshego vdol' reki vetra.

Nazad| Vpered

Publikacii s klyuchevymi slovami: kolebaniya - volny Publikacii so slovami: kolebaniya - volny
Sm. takzhe: Eho iz glubin krasnogo giganta

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce