Astronet > Kolebaniya i volny

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Kolebaniya i volny. Lekcii.

V.A.Aleshkevich, L.G.Dedenko, V.A.Karavaev (Fizicheskii fakul'tet MGU)
Izdatel'stvo Fizicheskogo fakul'teta MGU, 2001 g. Soderzhanie

Svobodnye nezatuhayushie kolebaniya v sistemah s dvumya stepenyami svobody. Normal'nye kolebaniya (mody). Parcial'nye i normal'nye chastoty. Bieniya. Ponyatie spektra kolebanii. Metodika analiza kolebanii 2-h svyazannyh oscillyatorov. Zatuhanie kolebanii i dissipaciya energii. Vynuzhdennye kolebaniya. Rezonans. Kolebaniya sistem so mnogimi stepenyami svobody. Dispersionnoe sootnoshenie.

Nablyudaya kolebaniya massy $m,$ podveshennoi na legkoi pruzhine zhestkosti $k_{1},$ nel'zya ne obratit' vnimanie na to, chto, naryadu s vertikal'nymi kolebaniyami gruza, voznikayut i tak nazyvaemye mayatnikovye kolebaniya (iz storony v storonu) (ris. 3.1).

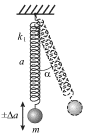Ris. 3.1.

Naibolee sil'nymi eti mayatnikovye kolebaniya budut togda, kogda chastota vertikal'nyh kolebanii $\sqrt {\displaystyle k_{1} / m}$ budet ravna udvoennoi chastote mayatnikovyh kolebanii $\sqrt {\displaystyle g / a}$ ( $a$ - dlina rastyanutoi pruzhiny pri nepodvizhnom gruze). Takoi rezul'tat legko ponyat', esli rassmatrivat' mayatnikovye kolebaniya kak rezonansnye parametricheskie kolebaniya, pri etom parametr mayatnika - dlina pruzhiny $a$ - menyaetsya pri vertikal'nyh kolebaniyah na velichinu $\pm \Delta a$ (sm. predydushuyu lekciyu). V techenie nekotorogo vremeni mayatnikovye kolebaniya mogut usilivat'sya za schet umen'sheniya energii vertikal'nyh kolebanii. Zatem process poidet v obratnom napravlenii: mayatnikovye kolebaniya nachnut oslabevat', "vozvrashaya" energiyu usilivayushimsya vertikal'nym kolebaniyam. Sledovatel'no, vertikal'nye kolebaniya ne budut garmonicheskimi, chto svyazano s nalichiem mayatnikovyh kolebanii, sootvetstvuyushih vozbuzhdeniyu vtoroi stepeni svobody. Pri opredelennyh usloviyah mogut voznikat' i krutil'nye kolebaniya gruza vokrug vertikal'noi osi pruzhiny. Opyt pokazyvaet, chto naibolee sil'nymi eti kolebaniya budut v tom sluchae, kogda ih chastota $\sqrt {\displaystyle k_{2} / J} (k_{2}$ - koefficient zhestkosti pruzhiny pri ee skruchivanii, rassmotrennyi v lekcii po deformacii tverdogo tela, $J$ - moment inercii tela otnositel'no vertikal'noi osi) budet primerno v dva raza men'she chastoty vertikal'nyh kolebanii. V obshem sluchae v etoi sisteme mogut proishodit' chetyre tipa kolebanii, sootvetstvuyushih chetyrem stepenyam svobody: odno vertikal'noe, dva mayatnikovyh v dvuh vzaimno-perpendikulyarnyh ploskostyah i odno krutil'noe.

Takim obrazom, pered nami voznikaet zadacha izucheniya osnovnyh zakonomernostei kolebanii v sistemah s dvumya, tremya i bolee stepenyami svobody, zatem mozhno rassmotret' i kolebaniya sploshnoi sredy, kak sistemy s beskonechno bol'shim chislom stepenei svobody.

Svobodnye nezatuhayushie kolebaniya v sistemah s dvumya stepenyami svobody.

Na ris. 3.2 izobrazheny tri razlichnye kolebatel'nye sistemy s dvumya stepenyami svobody. Pervaya iz nih (a) - eto dva razlichnyh pruzhinnyh mayatnika, svyazannye pruzhinoi s zhestkost'yu ${\displaystyle k}'.$ Vtoraya (b) - dva gruza s massami $m_{1}$ i $m_{2} ,$ zakreplennye na natyanutom nekotoroi siloi $F$ nevesomom rezinovom shnure. Tret'ya (v) - dva svyazannyh pruzhinoi ${\displaystyle k}'$ razlichnyh mayatnika, kazhdyi iz kotoryh sostoit iz gruza, podveshennogo na nevesomom sterzhne.

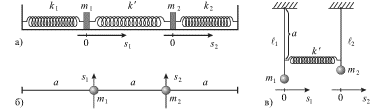Ris. 3.2.

Kolebaniya gruzov v kazhdoi iz treh sistem opisyvayutsya dvumya vremennymi zavisimostyami ih smeshenii $s_{1} (t)$ i $s_{2} (t).$ Polozhitel'noe napravlenie smesheniya $s$ na risunke ukazano strelkami.

Opyt pokazyvaet, chto pri proizvol'nom sposobe vozbuzhdeniya kolebaniya ne budut garmonicheskimi: amplituda kolebanii kazhdoi iz mass budet periodicheski menyat'sya vo vremeni. Odnako mozhno sozdat' takie nachal'nye usloviya, pri kotoryh kazhdyi gruz budet sovershat' garmonicheskie kolebaniya s odnoi i toi zhe chastotoi $\omega$ :

(3.1)

$\begin{array}{l} s_{1} (t) = s_{01} \sin (\omega t + \varphi ); \\ s_{2} (t) = s_{02} \sin (\omega t + \varphi ). \\ \end{array}$

Chastota etih kolebanii \omega opredelyaetsya svoistvami sistemy. Otnoshenie

(3.2)

$\varsigma = s_{02} / s_{01}$

takzhe opredelyaetsya parametrami sistemy. Eta bezrazmernaya algebraicheskaya velichina $\varsigma$ nazyvaetsya koefficientom raspredeleniya amplitud pri garmonicheskom kolebanii. Otmetim, chto $s_{01}$ i $s_{02}$ mogut imet' lyuboi znak. Esli $\varsigma \gt 0,$ to smesheniya obeih mass vsegda proishodit v odnu storonu (sinfaznye kolebaniya), a pri $\varsigma \lt 0$ - v protivopolozhnye storony (protivofaznye kolebaniya). Garmonicheskie kolebaniya (3.1) nazyvayutsya normal'nymi kolebaniyami, ili modami, a chastota $\omega$ nazyvaetsya normal'noi chastotoi. Takim obrazom, moda harakterizuetsya dvumya parametrami: chastotoi $\omega$ i koefficientom $\varsigma ,$ opredelyayushim "konfiguraciyu" mody.

Praktika pokazyvaet, chto v sisteme s dvumya stepenyami svobody mogut sushestvovat' sinfaznye garmonicheskie kolebaniya s chastotoi $\omega _{I}$ i protivofaznye garmonicheskie kolebaniya s chastotoi $\omega _{II} \gt \omega _{I} .$

Sledovatel'no, v sisteme mogut byt' vozbuzhdeny dve mody:

I moda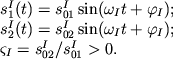

$\begin{array}{l} s_{1}^{I} (t) = s_{01}^{I} \sin (\omega _{I} t + \varphi _{I} ); \\ s_{2}^{I} (t) = s_{02}^{I} \sin (\omega _{I} t + \varphi _{I} ); \\ \varsigma _{I} = s_{02}^{I} / s_{01}^{I} \gt 0. \\ \end{array}$

(3.3)

II moda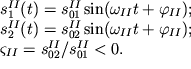

$\begin{array}{l} s_{1}^{II} (t) = s_{01}^{II} \sin (\omega _{II} t + \varphi _{II} ); \\ s_{2}^{II} (t) = s_{02}^{II} \sin (\omega _{II} t + \varphi _{II} ); \\ \varsigma _{II} = s_{02}^{II} / s_{01}^{II} \lt 0. \\ \end{array}$

(3.4)

Netrudno teper' ponyat', chto lyuboe kolebanie svyazannoi lineinoi sistemy s dvumya stepenyami svobody (a imenno takie sistemy my budem dalee rassmatrivat') mozhet byt' predstavleno v vide superpozicii dvuh normal'nyh kolebanii (3.3) i (3.4):

(3.5)

$\begin{array}{l} s_{1} (t) = s_{1}^{I} (t) + s_{1}^{II} (t) = s_{01}^{I} \sin (\omega _{I} t + \varphi _{I} ) + s_{01}^{II} \sin (\omega _{II} t + \varphi _{II} ); \\ s_{2} (t) = s_{2}^{I} (t) + s_{2}^{II} (t) = s_{02}^{I} \sin (\omega _{I} t + \varphi _{I} ) + s_{02}^{II} \sin (\omega _{II} t + \varphi _{II} ). \\ \end{array}$

Ne pribegaya poka k detal'nomu matematicheskomu issledovaniyu, proanaliziruem povedenie sistemy s dvumya stepenyami svobody, pol'zuyas' osnovnymi ideyami, razvitymi v predydushih lekciyah. Predstavim lyubuyu iz sistem, izobrazhennyh na ris. 3.2, kak slozhnuyu sistemu, sostoyashuyu iz dvuh parcial'nyh sistem. Eti parcial'nye sistemy, sootvetstvuyushie sluchayu (a) ris. 3.2, pokazany na ris. 3.3: kazhdaya iz etih parcial'nyh sistem imeet sobstvennuyu chastotu kolebanii, kotoraya nazyvaetsya parcial'noi chastotoi.

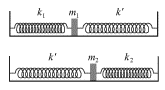Ris. 3.3.

Velichiny etih parcial'nyh chastot, sootvetstvenno, ravny:

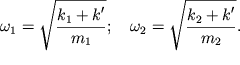(3.6)

$\omega _{1} = \sqrt {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle k_{1} + {\displaystyle k}'}}{\displaystyle {\displaystyle m_{1} }}}} ; \quad \omega _{2} = \sqrt {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle k_{2} + {\displaystyle k}'}}{\displaystyle {\displaystyle m_{2} }}}} .$

Sovershenno ochevidno, chto chastota $\omega _{1}$ - eto chastota kolebanii massy $m_{1}$ v sisteme dvuh svyazannyh mayatnikov, kogda massa $m_{2}$ nepodvizhna (zablokirovana vtoraya stepen' svobody). Analogichno, s chastotoi $\omega _{2}$ budet kolebat'sya massa $m_{2} ,$ kogda nepodvizhna massa $m_{1} .$

Teper' pereidem k opredeleniyu normal'nyh chastot $\omega _{I}$ i $\omega _{II} .$ Vspomnim, chto kvadrat chastoty garmonicheskih kolebanii raven otnosheniyu vozvrashayushei sily k smesheniyu gruza $s$ i velichine ego massy $m.$ Podberem nachal'nye smesheniya mass $m_{1}$ i $m_{2}$ takim obrazom, chtoby dlya obeih mass eti otnosheniya (a, sledovatel'no, i chastoty) byli by odinakovy. Takoi podbor legko ugadyvaetsya dlya simmetrichnoi sistemy $(m_{1} = m_{2} = m, k_{1} = k_{2} = k),$ (ris. 3.4), u kotoroi parcial'nye chastoty sovpadayut:

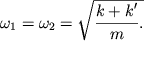(3.7)

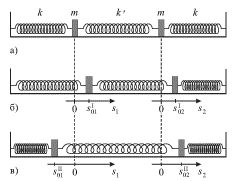$\omega _{1} = \omega _{2} = \sqrt {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle k + {\displaystyle k}'}}{\displaystyle {\displaystyle m}}}.}$

Ris. 3.4

Esli oba gruza smestit' vpravo na odinakovye rasstoyaniya $s_{01}^{I} = s_{02}^{I} ,$ to srednyaya pruzhina ${\displaystyle k}'$ (pruzhina svyazi) ne budet deformirovana (poziciya b). Posle otpuskaniya pruzhina budet ostavat'sya nedeformirovannoi. Poetomu kazhdyi iz gruzov budet sovershat' garmonicheskie kolebaniya s odnoi i toi zhe chastotoi

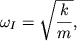(3.8)

$\omega _{I} = \sqrt {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle k}}{\displaystyle {\displaystyle m}}}} ,$

kotoraya i yavlyaetsya pervoi normal'noi chastotoi. Konfiguraciya etogo sinfaznogo kolebaniya (mody) zadaetsya koefficientom raspredeleniya amplitud $\varsigma _{I} = + 1.$

Esli teper' obe massy smestit' v raznye storony na odinakovye rasstoyaniya $s_{02}^{II} = - s_{01}^{II}$ (poziciya v), to pruzhina ${\displaystyle k}'$ udlinitsya na velichinu $2s_{02}^{II} .$ Poetomu k pravoi masse budet prilozhena vozvrashayushaya sila, ravnaya $- (ks_{02}^{II} + 2{\displaystyle k}'s_{02}^{II} ),$ a na levuyu massu budet deistvovat' v protivopolozhnom napravlenii sila $- (ks_{01}^{II} + 2{\displaystyle k}'s_{01}^{II} ).$ Posle otpuskaniya gruzy budut sovershat' protivofaznye garmonicheskie kolebaniya so vtoroi normal'noi chastotoi

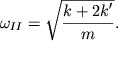(3.9)

$\omega _{II} = \sqrt {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle k + 2{\displaystyle k}'}}{\displaystyle {\displaystyle m}}}} .$

Konfiguraciya vtoroi mody harakterizuetsya koefficientom raspredeleniya $\varsigma _{II} = - 1.$

Nazad| Vpered

Publikacii s klyuchevymi slovami: kolebaniya - volny Publikacii so slovami: kolebaniya - volny
Sm. takzhe: Eho iz glubin krasnogo giganta

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

Kolebaniya i volny. Lekcii.

Lekciya 3

Svobodnye nezatuhayushie kolebaniya v sistemah s dvumya stepenyami svobody.