Astronet > Kolebaniya i volny

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Kolebaniya i volny. Lekcii.

V.A.Aleshkevich, L.G.Dedenko, V.A.Karavaev (Fizicheskii fakul'tet MGU)
Izdatel'stvo Fizicheskogo fakul'teta MGU, 2001 g. Soderzhanie

Esli gruzy, izobrazhennye na ris. 3.5a, smestit' na proizvol'nye rasstoyaniya (naprimer, v odnu storonu na velichiny $s_{01}$ i $s_{02} ,$ kak eto izobrazheno na ris. 3.5b), to eto ekvivalentno superpozicii dvuh tipov nachal'nyh smeshenii: v odnu storonu na odinakovye velichiny (poziciya v)

(3.10)

$s_{01}^{I} = s_{02}^{I} = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}(s_{01} + s_{02} );$

i v raznye storony (poziciya g) na velichiny

(3.11)

$- s_{01}^{II} = s_{02}^{II} = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}(s_{02} - s_{01} ).$

Poskol'ku kolebatel'naya sistema lineina, to sinfaznye kolebaniya, voznikayushie posle otpuskaniya gruzov v pozicii (v), budut proishodit' nezavisimo ot prisutstviya protivofaznyh kolebanii, voznikayushih pri otpuskanii gruzov v pozicii (g). Smesheniya oboih gruzov s techeniem vremeni budut opisyvat'sya formulami (3.5), v kotoryh amplitudy opredelyayutsya ravenstvami (3.10) i (3.11), a nachal'nye fazy $\varphi _{I} = \varphi _{II} = \pi / 2.$

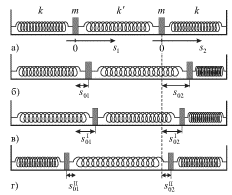Ris. 3.5.

Proanaliziruem bolee podrobno kolebaniya v sisteme, izobrazhennoi na ris. 3.5. Pust' my sdvinuli levuyu massu vpravo na rasstoyanie $s_{01} ,$ a pravuyu massu ostavim v nesmeshennom polozhenii $(s_{02} = 0).$ Posle otpuskaniya oboih gruzov v sisteme vozniknut kolebaniya. Iz (3.10) i (3.11) opredelyaem amplitudy mod: $s_{01}^{I} = s_{02}^{I} = s_{01} / 2; - s_{01}^{II} = s_{02}^{II} = - s_{01} / 2.$ Poskol'ku fazy $\varphi _{I} = \varphi _{II} = \pi / 2$ (t.k. nachal'nye skorosti u gruzov otsutstvuyut), to smesheniya

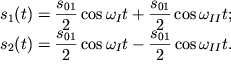(3.12)

$\begin{array}{l} s_{1} (t) = {\displaystyle \frac{\displaystyle {\displaystyle s_{01} }}{\displaystyle {\displaystyle 2}}}\cos \omega _{I} t + {\displaystyle \frac{\displaystyle {\displaystyle s_{01} }}{\displaystyle {\displaystyle 2}}}\cos \omega _{II} t; \\ s_{2} (t) = {\displaystyle \frac{\displaystyle {\displaystyle s_{01} }}{\displaystyle {\displaystyle 2}}}\cos \omega _{I} t - {\displaystyle \frac{\displaystyle {\displaystyle s_{01} }}{\displaystyle {\displaystyle 2}}}\cos \omega _{II} t. \\ \end{array}$

Proizvodya summirovanie trigonometricheskih funkcii v (3.12), poluchim:

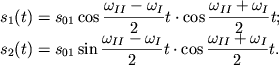(3.13)

$\begin{array}{l} s_{1} (t) = s_{01} \cos {\displaystyle \frac{\displaystyle {\displaystyle \omega _{II} - \omega _{I} }}{\displaystyle {\displaystyle 2}}}t \cdot \cos {\displaystyle \frac{\displaystyle {\displaystyle \omega _{II} + \omega _{I} }}{\displaystyle {\displaystyle 2}}}t; \\ s_{2} (t) = s_{01} \sin {\displaystyle \frac{\displaystyle {\displaystyle \omega _{II} - \omega _{I} }}{\displaystyle {\displaystyle 2}}}t \cdot \cos {\displaystyle \frac{\displaystyle {\displaystyle \omega _{II} + \omega _{I} }}{\displaystyle {\displaystyle 2}}}t. \\ \end{array}$

Vremennye zavisimosti (3.13) izobrazheny na ris. 3.6.

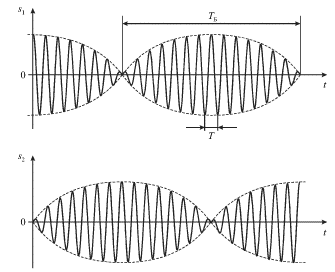Ris. 3.6.

Vidno, chto kolebaniya kazhdoi iz mass imeyut formu bienii. Period etih bienii raven¹

(3.14)

$T_{b} = {\displaystyle \frac{\displaystyle {\displaystyle 2\pi }}{\displaystyle {\displaystyle \omega _{II} - \omega _{I} }}} = {\displaystyle \frac{\displaystyle {\displaystyle 2\pi }}{\displaystyle {\displaystyle \Omega _{b} }}},$

gde chastota bienii

(3.15)

$\Omega _{b} = \Delta \omega = \omega _{II} - \omega _{I} .$

Esli vvesti srednyuyu chastotu

(3.16)

$\omega _{0} = {\displaystyle \frac{\displaystyle {\displaystyle \omega _{I} + \omega _{II} }}{\displaystyle {\displaystyle 2}}},$

to s etoi chastotoi svyazan period kolebanii $T = {\displaystyle \frac{\displaystyle {\displaystyle 2\pi }}{\displaystyle {\displaystyle \omega _{0} }}}.$

Esli chastota bienii $\Omega _{b} \ll \omega _{0} ,$ kak eto izobrazheno na ris. 3.6, to $T_{b} \gg T.$ V etom sluchae kolebaniya oboih gruzov budut pochti garmonicheskimi (kvazigarmonicheskimi). Esli perepisat' (3.13) s ispol'zovaniem srednei chastoty $\omega _{0}$ i chastoty bienii $\Omega _{b}$ v vide:

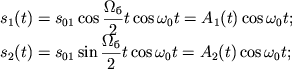(3.17)

$\begin{array}{l} s_{1} (t) = s_{01} \cos {\displaystyle \frac{\displaystyle {\displaystyle \Omega _{b} }}{\displaystyle {\displaystyle 2}}}t\cos \omega _{0} t = A_{1} (t)\cos \omega _{0} t; \\ s_{2} (t) = s_{01} \sin {\displaystyle \frac{\displaystyle {\displaystyle \Omega _{b} }}{\displaystyle {\displaystyle 2}}}t\cos \omega _{0} t = A_{2} (t)\cos \omega _{0} t; \\ \end{array}$

to pri $\Omega _{b} \ll \omega _{0}$ kolebaniya (3.17) mozhno traktovat' kak kolebaniya s chastotoi $\omega _{0}$ i medlenno menyayusheisya amplitudoi $A(t).$

V teorii kolebanii i v drugih razdelah fiziki dlya analiza kolebatel'nogo processa ispol'zuyut spektral'noe predstavlenie, ili spektr kolebanii. Etot spektr izobrazhayut graficheski, gde po osi absciss ukazyvayut chastoty kolebanii, a po osi ordinat otkladyvayut kvadraty ih amplitud. Tak, v chastnosti, dlya kolebanii, izobrazhennyh na ris. 3.6 ( $s_{1}$ ili $s_{2}$ ) i opisyvaemyh formulami (3.17), legko narisovat' spektr, poskol'ku uzhe izvestno spektral'noe razlozhenie etogo kolebaniya (predstavlenie v vide summy garmonicheskih kolebanii), zadavaemoe formulami (3.12).

Takoi spektr izobrazhen na ris. 3.7.

Ris. 3.7.

Etot spektr soderzhit dve spektral'nye komponenty. Ego mozhno oharakterizovat' srednei chastotoi $\omega _{0}$ i shirinoi $\Delta \omega .$ V sootvetstvii s formuloi (3.14) proizvedenie $\Delta \omega$ na period $T_{b}$ ravno postoyannoi velichine:

(3.18)

$\Delta \omega \cdot T_{b} = 2\pi .$

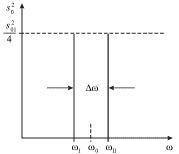
Formula (3.18) imeet glubokoe fizicheskoe soderzhanie. Tak, esli proishodit nekotoroe kvazigarmonicheskoe kolebanie vida

(3.19)

$s(t) = A(t)\cos [\omega _{0} t + \varphi (t)],$

dlya kotorogo amplituda $A$ i faza $\varphi$ medlenno menyayutsya na masshtabe vremeni $\tau$ (ris. 3.8a), to spektr takogo kolebaniya mozhet sostoyat' iz bol'shogo chisla chastot.

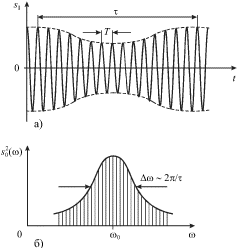Ris. 3.8.

Eti chastoty gruppiruyutsya vblizi central'noi (osnovnoi) chastoty $\omega _{0} = 2\pi / T$ v predelah harakternogo intervala chastot $\Delta \omega ,$ obratno proporcional'nogo vremennomu masshtabu $\tau .$ Na ris. 3.8b izobrazhen etot spektr, gde po osi ordinat otlozhen kvadrat amplitudy $s_{0}$ kazhdoi iz garmonicheskih sostavlyayushih, prichem mezhdu $\tau$ i $\Delta \omega$ sushestvuet svyaz': $\Delta \omega \cdot \tau \sim 2\pi .$

Kolichestvennaya svyaz' mezhdu kolebatel'nym processom $s(t)$ i ego spektrom predstavlyaetsya (po analogii s formulami (3.12)) v vide summy konechnogo ili beskonechnogo chisla garmonicheskih sostavlyayushih (v vide ryada ili integrala Fur'e). Takoe predstavlenie budet shiroko ispol'zovat'sya v kurse "Optika".

¹Kolebaniya (3.12), voobshe govorya, ne yavlyayutsya periodicheskimi, t.e. nel'zya ukazat' takoe vremya $T*,$ spustya kotoroe oni tochno povtoryayutsya (otnoshenie chastot $\omega _{I} / \omega _{II}$ - chashe vsego irracional'noe chislo, a sluchai ih racional'nogo otnosheniya: $m\omega _{I} = n\omega _{II}$ budut ischezayushe redki). Poetomu periodom bienii $T_{b}$ my nazyvaem period (3.14) povtoreniya ogibayushei summarnogo kolebaniya, ravnyi polovine perioda kolebaniya s chastotoi ${\displaystyle \frac{\displaystyle {\displaystyle \omega _{II} - \omega _{I} }}{\displaystyle {\displaystyle 2}}}, a \Omega _{b} = {\displaystyle \frac{\displaystyle {\displaystyle 2\pi }}{\displaystyle {\displaystyle T_{b} }}} = \omega _{II} - \omega _{I} .$

Nazad| Vpered

Publikacii s klyuchevymi slovami: kolebaniya - volny Publikacii so slovami: kolebaniya - volny
Sm. takzhe: Eho iz glubin krasnogo giganta

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce