Astronet > Kolebaniya i volny

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Kolebaniya i volny. Lekcii.

V.A.Aleshkevich, L.G.Dedenko, V.A.Karavaev (Fizicheskii fakul'tet MGU)
Izdatel'stvo Fizicheskogo fakul'teta MGU, 2001 g. Soderzhanie

Metodika analiza kolebanii svyazannyh oscillyatorov.

Vyshe my rassmotreli kolebaniya dvuh odinakovyh svyazannyh pruzhinnyh mayatnikov, ne pribegaya k resheniyu uravnenii ih dvizheniya. Odnako, esli zhestkosti pruzhin i massy tel imeyut proizvol'nye velichiny, to zachastuyu byvaet trudno dogadat'sya o konfiguracii mod i ih chastotah. Poetomu predstavlyaetsya vazhnym vooruzhit'sya universal'nym metodom, pozvolyayushim po edinoi sheme provesti posledovatel'nyi analiz lyuboi kolebatel'noi sistemy s dvumya stepenyami svobody, yavlyayusheisya sistemoi lyubyh svyazannyh oscillyatorov.

Zapishem uravneniya dvizheniya dvuh svyazannyh pruzhinnyh mayatnikov v vide:

(3.20)

$\begin{array}{l} m_{1} \ddot {\displaystyle s}_{1} = - k_{1} s_{1} - {\displaystyle k}'s_{1} + {\displaystyle k}'s_{2} ; \\ m_{2} \ddot {\displaystyle s}_{2} = - k_{2} s_{2} - {\displaystyle k}'s_{2} + {\displaystyle k}'s_{1} . \\ \end{array}$

Razdeliv pervoe uravnenie na $m_{1} ,$ a vtoroe - na $m_{2}$ i ispol'zuya vyrazheniya (3.6) dlya parcial'nyh chastot, perepishem (3.20) sleduyushim obrazom:

(3.21)

$\begin{array}{l} \ddot {\displaystyle s}_{1} = - \omega _{1}^{2} s_{1} - \alpha _{1} s_{2} , \\ \ddot {\displaystyle s}_{2} = - \alpha _{2} s_{1} - \omega _{2}^{2} s_{2} , \\ \end{array}$

gde $\alpha _{1} = - {\displaystyle k}' / m_{1} , \alpha _{2} = - {\displaystyle k}' / m_{2}$ - koefficienty, zavisyashie ot zhestkosti ${\displaystyle k}'$ pruzhiny svyazi. Obratim vnimanie, chto uravneniya (3.21) ne mogut reshat'sya po otdel'nosti, t.k. kazhdoe iz nih soderzhit $s_{1}$ i $s_{2} .$ Poetomu celesoobrazno pereiti ot smeshenii $s_{1}$ i $s_{2}$ k novym funkciyam $\xi _{1}$ i $\xi _{2} ,$ nazyvaemym normal'nymi koordinatami. Smysl perehoda sostoit v poluchenii dvuh nezavisimyh uravnenii dvizheniya, kotorye mozhno reshat' po otdel'nosti.

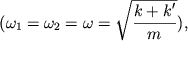Odnako, v obshem sluchae eti koordinaty naiti ne prosto. 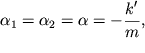Poetomu dlya illyustracii takogo perehoda rassmotrim sistemu s odinakovymi massami $(m_{1} = m_{2} = m)$ i pruzhinami $(k_{1} = k_{2} = k).$ Poskol'ku parcial'nye chastoty sovpadayut $(\omega _{1} = \omega _{2} = \omega = \sqrt {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle k + {\displaystyle k}'}}{\displaystyle {\displaystyle m}}}} ),$ a takzhe $\alpha _{1} = \alpha _{2} = \alpha = - {\displaystyle \frac{\displaystyle {\displaystyle {\displaystyle k}'}}{\displaystyle {\displaystyle m}}},$ to sistema uravnenii (3.21) stanovitsya bolee prostoi. Slozhiv oba uravneniya, poluchaem:

(3.22a)

$\ddot {\displaystyle \xi }_{1} = - (\omega ^{2} + \alpha )\xi _{1} ,$

gde $\xi _{1} = s_{1} + s_{2}$ - pervaya normal'naya koordinata. Vychitaya vtoroe uravnenie iz pervogo, nahodim:

(3.22b)

$\ddot {\displaystyle \xi }_{2} = - (\omega ^{2} - \alpha )\xi _{2} ,$

gde $\xi _{2} = s_{1} - s_{2}$ - vtoraya normal'naya koordinata. Teper' uravneniya (3.22) nezavisimy. Pervoe iz nih opisyvaet kolebanie centra mass sistemy s chastotoi

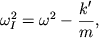(3.23)

$\omega _{I}^{2} = \omega ^{2} - {\displaystyle \frac{\displaystyle {\displaystyle {\displaystyle k}'}}{\displaystyle {\displaystyle m}}},$

men'shei parcial'noi chastoty $\omega .$ Vtoroe uravnenie opisyvaet izmenenie rasstoyaniya mezhdu dvumya massami s chastotoi

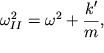(3.24)

$\omega _{II}^{2} = \omega ^{2} + {\displaystyle \frac{\displaystyle {\displaystyle {\displaystyle k}'}}{\displaystyle {\displaystyle m}}},$

prevyshayushei parcial'nuyu chastotu. Resheniya uravnenii (3.22) ochevidny:

(3.25a)

$\xi _{1} (t) = s_{1} (t) + s_{2} (t) = \xi _{01} \sin (\omega _{I} t + \varphi _{I} );$

(3.25b)

$\xi _{2} (t) = s_{1} (t) - s_{2} (t) = \xi _{02} \sin (\omega _{II} t + \varphi _{II} ).$

Vozvrashayas' k funkciyam $s_{1}$ i $s_{2} ,$ poluchaem:

(3.26a)

$s_{1} (t) = {\displaystyle \frac{\displaystyle {\displaystyle \xi _{01} }}{\displaystyle {\displaystyle 2}}}\sin (\omega _{I} t + \varphi _{I} ) + {\displaystyle \frac{\displaystyle {\displaystyle \xi _{02} }}{\displaystyle {\displaystyle 2}}}\sin (\omega _{II} t + \varphi _{II} );$

(3.26b)

$s_{2} (t) = {\displaystyle \frac{\displaystyle {\displaystyle \xi _{01} }}{\displaystyle {\displaystyle 2}}}\sin (\omega _{I} t + \varphi _{I} ) - {\displaystyle \frac{\displaystyle {\displaystyle \xi _{02} }}{\displaystyle {\displaystyle 2}}}\sin (\omega _{II} t + \varphi _{II} ).$

Chetyre velichiny $\xi _{01} , \xi _{02} , \varphi _{I} i \varphi _{II}$ opredelyayutsya iz nachal'nyh uslovii: $s_{1} (t = 0), s_{2} (t = 0), \dot {\displaystyle s}_{1} (t = 0), \dot {\displaystyle s}_{2} (t = 0).$

Proillyustrirovav perehod k normal'nym koordinatam, vernemsya k metodike analiza kolebanii v proizvol'nyh sistemah, opisyvaemyh uravneniyami (3.21).

Pust' v sisteme proishodit normal'noe kolebanie s neizvestnoi poka chastotoi $\omega$ i koefficientom raspredeleniya amplitud $\varsigma = {\displaystyle \frac{\displaystyle {\displaystyle s_{02} }}{\displaystyle {\displaystyle s_{01} }}}$ :

(3.27)

$s_{1} (t) = s_{01} \sin (\omega t + \varphi ), \quad s_{2} (t) = s_{02} \sin (\omega t + \varphi ).$

Podstavim (3.27) v sistemu uravnenii (3.21). Togda poluchim sistemu iz dvuh algebraicheskih uravnenii:

(3.28)

$\begin{array}{l} (\omega _{1}^{2} - \omega ^{2})s_{01} + \alpha _{1} s_{02} = 0; \\ \alpha _{2} s_{01} + (\omega _{2}^{2} - \omega ^{2})s_{02} = 0. \\ \end{array}$

Sistema lineinyh odnorodnyh uravnenii (3.28) imeet otlichnye ot nulya resheniya tol'ko v tom sluchae, esli ee opredelitel' raven nulyu:

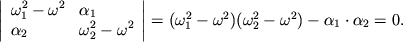(3.29)

${\displaystyle \left| {\displaystyle {\displaystyle \begin{array}{ *{20}c} {\displaystyle \omega _{1}^{2} - \omega ^{2}} \hfill & {\displaystyle \alpha _{1} } \hfill \\ {\displaystyle \alpha _{2} } \hfill & {\displaystyle \omega _{2}^{2} - \omega ^{2}} \hfill \\ \end{array} }} \right|} = (\omega _{1}^{2} - \omega ^{2})(\omega _{2}^{2} - \omega ^{2}) - \alpha _{1} \cdot \alpha _{2} = 0.$

Eto - kvadratnoe uravnenie otnositel'no $\omega ^{2},$ prichem $\omega \gt 0.$ Poetomu, reshaya uravnenie (3.29), mozhno naiti normal'nye chastoty $\omega _{I}$ i $\omega _{II} .$ Posle nahozhdeniya chastot ne sostavlyaet truda naiti konfiguraciyu mod, t.e. koefficienty raspredeleniya amplitud $\varsigma _{I}$ i $\varsigma _{II} .$ Ih mozhno opredelit', naprimer, iz pervogo uravneniya (3.28), prichem ochevidno, chto dlya kazhdoi normal'noi chastoty ( $\omega _{I}$ ili $\omega _{II}$ ) eti koefficienty razlichny:

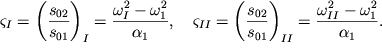(3.30)

$\varsigma _{I} = \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle s_{02} }}{\displaystyle {\displaystyle s_{01} }}}} \right)_{I} = {\displaystyle \frac{\displaystyle {\displaystyle \omega _{I}^{2} - \omega _{1}^{2} }}{\displaystyle {\displaystyle \alpha _{1} }}}, \quad \varsigma _{II} = \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle s_{02} }}{\displaystyle {\displaystyle s_{01} }}}} \right)_{II} = {\displaystyle \frac{\displaystyle {\displaystyle \omega _{II}^{2} - \omega _{1}^{2} }}{\displaystyle {\displaystyle \alpha _{1} }}}.$

Takim obrazom, uravnenie (3.29) i ravenstvo (3.30) pozvolyayut polnost'yu rasschitat' parametry kazhdoi iz dvuh mod. Dvizhenie kazhdoi iz mass, kak uzhe neodnokratno otmechalos', yavlyaetsya superpoziciei dvuh normal'nyh kolebanii:

$s_{1} (t) = s_{01_{I} } \sin (\omega _{I} t + \varphi _{I} ) + s_{01_{II} } \sin (\omega _{II} t + \varphi _{II} ),$

$s_{2} (t) = \varsigma _{I} \cdot s_{01_{I} } \sin (\omega _{I} t + \varphi _{I} ) + \varsigma _{II} \cdot s_{01_{II} } \sin (\omega _{II} t + \varphi _{II} ),$

gde amplitudy $s_{01_{I} }$ i $s_{01_{II} }$ i nachal'nye fazy $\varphi _{I}$ i $\varphi _{II}$ opredelyayutsya, kak i ran'she, iz nachal'nyh uslovii: $s_{1} (0), s_{2} (0), \dot {\displaystyle s}_{1} (0), \dot {\displaystyle s}_{2} (0).$

Raschet mod dlya lyuboi sistemy dvuh svyazannyh oscillyatorov chitatel' mozhet prodelat' samostoyatel'no.

Sootnoshenie mezhdu parcial'nymi i normal'nymi chastotami.

Dlya ustanovleniya svyazi mezhdu parcial'nymi i normal'nymi chastotami perepishem (3.29) v vide

(3.31)

$(\omega _{1}^{2} - \omega ^{2})(\omega _{2}^{2} - \omega ^{2}) - \gamma ^{2}\omega _{1}^{2} \omega _{2}^{2} = 0,$

gde

(3.32)

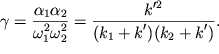$\gamma = {\displaystyle \frac{\displaystyle {\displaystyle \alpha _{1} \alpha _{2} }}{\displaystyle {\displaystyle \omega _{1}^{2} \omega _{2}^{2} }}} = {\displaystyle \frac{\displaystyle {\displaystyle {\displaystyle k}'^{2}}}{\displaystyle {\displaystyle (k_{1} + {\displaystyle k}')(k_{2} + {\displaystyle k}')}}}.$

Bezrazmernyi koefficient svyazi \gamma mezhdu dvumya sistemami mozhet prinimat' znacheniya $0 \lt \gamma \lt 1.$ Esli iz (3.31) opredelit' normal'nye chastoty $\omega _{I}$ i $\omega _{II} ,$ to oni budut vyrazhat'sya cherez parcial'nye chastoty $\omega _{1}$ i $\omega _{2}$ i koefficient $\gamma .$ Eti chetyre chastoty budut raspolagat'sya na osi chastot v posledovatel'nosti, izobrazhennoi na ris. 3.9.

Ris. 3.9.

Pri slaboi svyazi $(\gamma \ll 1)$ normal'nye chastoty blizki k parcial'nym, a pri sil'noi svyazi $(\gamma \leq 1)$ razlichie v chastotah stanovitsya sushestvennym. Eto horosho vidno, esli parcial'nye chastoty sovpadayut $\left( {\displaystyle \omega _{1} = \omega _{2} = \omega _{0} } \right).$ Togda (3.31) primet vid:

$(\omega _{0}^{2} - \omega ^{2})^{2} - \gamma ^{2}\omega _{0}^{4} = 0.$

Otsyuda

(3.33)

$\omega _{I}^{2} = \omega _{0}^{2} \left( {\displaystyle 1 - \gamma } \right), \quad \omega _{II}^{2} = \omega _{0}^{2} \left( {\displaystyle 1 + \gamma } \right).$

Nazad| Vpered

Publikacii s klyuchevymi slovami: kolebaniya - volny Publikacii so slovami: kolebaniya - volny
Sm. takzhe: Eho iz glubin krasnogo giganta

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce