Astronet > Kolebaniya i volny

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Kolebaniya i volny. Lekcii.

V.A.Aleshkevich, L.G.Dedenko, V.A.Karavaev (Fizicheskii fakul'tet MGU)
Izdatel'stvo Fizicheskogo fakul'teta MGU, 2001 g. Soderzhanie

Esli energiya ne podvoditsya izvne, to kolebaniya svyazannyh oscillyatorov budut zatuhat'. Poskol'ku sila vyazkogo treniya proporcional'na skorosti, to uravneniya (3.21) s uchetom zatuhaniya primut vid:

(3.34)

$\begin{array}{l} \ddot {\displaystyle s}_{1} = - \omega _{1}^{2} s_{1} - 2\delta _{1} \dot {\displaystyle s}_{1} - \alpha _{1} s_{2} , \\ \ddot {\displaystyle s}_{2} = - \alpha _{2} s_{1} - \omega _{2}^{2} s_{2} - 2\delta _{2} \dot {\displaystyle s}_{2} . \\ \end{array}$

Zdes' $\delta _{1} = \Gamma _{1} / 2m_{1}$ i $\delta _{2} = \Gamma _{2} / 2m_{2}$ - koefficienty zatuhaniya dlya pervogo i vtorogo oscillyatorov. Esli iskat' reshenie etoi sistemy v vide normal'nyh zatuhayushih kolebanii:

(3.35)

$s_{1} \left( {\displaystyle t} \right) = s_{01} e^{ - \delta t}\sin \left( {\displaystyle \omega t + \varphi } \right), \quad s_{2} \left( {\displaystyle t} \right) = s_{02} e^{ - \delta t}\sin \left( {\displaystyle \omega t + \varphi } \right),$

to posle podstanovki (3.35) v (3.34) mozhno naiti normal'nuyu chastotu $\omega$ , koefficient zatuhaniya $\delta$ i konfiguraciyu $\varsigma$ kazhdoi iz dvuh mod. Opuskaya promezhutochnye vykladki, otmetim, chto pri $\omega _{1} \gg \delta _{1}$ i $\omega _{2} \gg \delta _{2}$ (slaboe zatuhanie) normal'nye chastoty i raspredelenie amplitud v modah budut blizki k tem, chto i v otsutstvie zatuhaniya. Dlya koefficienta zatuhaniya $\delta$ poluchaetsya vyrazhenie:

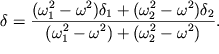(3.36)

$\delta = {\displaystyle \frac{\displaystyle {\displaystyle (\omega _{1}^{2} - \omega ^{2})\delta _{1} + (\omega _{2}^{2} - \omega ^{2})\delta _{2} }}{\displaystyle {\displaystyle (\omega _{1}^{2} - \omega ^{2}) + (\omega _{2}^{2} - \omega ^{2})}}}.$

Mozhno videt', chto pri proizvol'nom sootnoshenii mezhdu $\omega _{1} , \omega _{2} , \delta _{1}$ i $\delta _{2}$ koefficienty zatuhaniya mod $\delta _{I}$ i $\delta _{II} ,$ poluchaemye iz (3.36) pri $\omega = \omega _{I}$ i $\omega = \omega _{II} ,$ budut razlichnymi.

Esli parcial'nye chastoty sovpadayut $(\omega _{1} = \omega _{2} ),$ to

(3.37)

$\delta _{I} = \delta _{II} = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}\left( {\displaystyle \delta _{1} + \delta _{2} } \right).$

Esli $\omega _{1} \ne \omega _{2} ,$ a $\delta _{1} = \delta _{2} = \delta ,$ to

(3.38)

$\delta _{I} = \delta _{II} = \delta .$

Poslednim rezul'tatom my vospol'zuemsya pri rassmotrenii dissipacii energii v svyazannoi kolebatel'noi sisteme.

Energiya kolebatel'noi sistemy i ee dissipaciya.

Rassmotrim kolebaniya dvuh odinakovyh mass (ris. 3.10a), zakreplennyh na rastyanutom legkom rezinovom shnure.

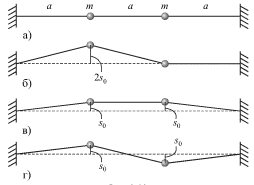Ris. 3.10.

Esli odin iz gruzov ottyanut' na rasstoyanie $2s_{0}$ (b) i zatem odnovremenno otpustit' obe massy, to ih kolebaniya budut imet' vid bienii. S drugoi storony, pri etih nachal'nyh usloviyah budut vozbuzhdeny dve mody (v i g) s odinakovymi amplitudami kolebanii obeih mass, ravnymi $s_{0} .$ Energiya, zapasennaya v pervoi mode, ravna summe kineticheskih energii obeih mass pri prohozhdenii imi polozheniya ravnovesiya so skorost'yu $v_{0}^{I} = s_{0} \omega _{I} ,$ t.e.:

(3.39a)

$E_{0}^{I} = 2{\displaystyle \frac{\displaystyle {\displaystyle m}}{\displaystyle {\displaystyle 2}}}(v_{0}^{I} )^{2} = ms_{0}^{2} \omega _{I}^{2} ,$

a energiya vtoroi mody, analogichno, ravna

(3.39b)

$E_{0}^{II} = 2{\displaystyle \frac{\displaystyle {\displaystyle m}}{\displaystyle {\displaystyle 2}}}(v_{0}^{II} )^{2} = ms_{0}^{2} \omega _{II}^{2} .$

Vazhno otmetit', chto energoobmen mezhdu modami otsutstvuet, a polnaya energiya sistemy ravna summe energii ee mod. V to zhe vremya v processe bienii energiya pervogo oscillyatora za vremya, ravnoe polovine perioda bienii, "peretekaet" ko vtoromu oscillyatoru i zatem za takoe zhe vremya vozvrashaetsya obratno. Polnyi energoobmen mezhdu oscillyatorami vozmozhen lish' togda, kogda obe massy odinakovy i otnoshenie $(\omega _{I} + \omega _{II} ) / (\omega _{II} - \omega _{I} )$ ravno celomu chislu $n,$ t.e.:

(3.40)

${\displaystyle \frac{\displaystyle {\displaystyle \omega _{I} + \omega _{II} }}{\displaystyle {\displaystyle \omega _{II} - \omega _{I} }}} = {\displaystyle \frac{\displaystyle {\displaystyle 2\omega _{0} }}{\displaystyle {\displaystyle \Omega _{b} }}} = n.$

Sledovatel'no, chastota $\omega _{0}$ dolzhna byt' kratnoi chastote bienii. V samom dele, pri vypolnenii usloviya (3.40) kazhdaya iz mass budet periodicheski ostanavlivat'sya v polozhenii ravnovesiya (kak sleduet iz formul (3.17)). S techeniem vremeni kolebaniya budut zatuhat', i budet eksponencial'no umen'shat'sya energiya, zapasennaya v modah:

(3.41a)

$E^{I}(t) = ms_{0}^{2} e^{ - 2\delta t}\omega _{I}^{2} = E_{0}^{I} e^{ - 2\delta t},$

(3.41b)

$E^{II}(t) = ms_{0}^{2} e^{ - 2\delta t}\omega _{II}^{2} = E_{0}^{II} e^{ - 2\delta t}.$

Vazhno podcherknut', chto cherez vremya $\tau _{E} = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2\delta }}}$ energiya kazhdoi iz mod umen'shitsya v e raz, pri etom protivofaznaya moda "poteryaet" bol'she energii, chem sinfaznaya, poskol'ku nachal'naya energiya $E_{0}^{II}$ u nee byla bol'she, chem $E_{0}^{I}$ (sm. (3.39)).

Vynuzhdennye kolebaniya.

Rassmotrim osnovnye zakonomernosti vynuzhdennyh ustanovivshihsya kolebanii v sisteme, izobrazhennoi na ris. 3.11, esli na levuyu massu $m_{1}$ deistvuet sila $F\left( {\displaystyle t} \right) = F_{0} \sin \omega t.$ Uravneniya dvizheniya v etom sluchae budut otlichat'sya ot (3.34) nalichiem etoi sily v pravoi chasti pervogo uravneniya:

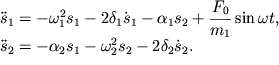(3.42)

$\begin{array}{l} \ddot {\displaystyle s}_{1} = - \omega _{1}^{2} s_{1} - 2\delta _{1} \dot {\displaystyle s}_{1} - \alpha _{1} s_{2} + {\displaystyle \frac{\displaystyle {\displaystyle F_{0} }}{\displaystyle {\displaystyle m_{1} }}}\sin \omega t, \\ \ddot {\displaystyle s}_{2} = - \alpha _{2} s_{1} - \omega _{2}^{2} s_{2} - 2\delta _{2} \dot {\displaystyle s}_{2} . \\ \end{array}$

Netrudno dogadat'sya, chto resheniyami etoi sistemy v ustanovivshemsya rezhime yavlyayutsya garmonicheskie funkcii

(3.43)

$s_{1} (t) = s_{01} \sin (\omega t + \varphi _{1} ), \quad s_{2} (t) = s_{02} \sin (\omega t + \varphi _{2} ),$

kotorye otrazhayut tot fakt, chto obe massy koleblyutsya na chastote vynuzhdayushei sily. Podstavlyaya (3.43) v (3.42), mozhno vychislit' amplitudy i fazy vynuzhdennyh kolebanii. My ogranichimsya lish' obsuzhdeniem rezul'tatov.

Ris. 3.11.

Na ris. 3.12 izobrazhena AChH dlya pervogo oscillyatora, k kotoromu prilozhena sila. Obrashaet na sebya vnimanie nalichie dvuh rezonansov, kotorye pri malom zatuhanii nablyudayutsya na normal'nyh chastotah $\omega _{I}$ i $\omega _{II}$ . Pri izmenenii chastoty $\omega$ ot $\omega _{I}$ do $\omega _{II}$ amplituda $s_{01}$ padaet i dostigaet minimuma na vtoroi parcial'noi chastote $\omega _{2} ,$ pri etom s umen'sheniem zatuhaniya amplituda na etoi chastote stremitsya k nulyu. Eto obstoyatel'stvo ispol'zuyut dlya podavleniya otklika sistemy na deistvie vneshnei sily. V radiotehnike, gde ispol'zuyutsya svyazannye kolebatel'nye kontury, ih primenyayut kak fil'try i dempfery.

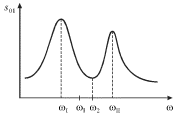Ris. 3.12.

Dva rezonansa imeyut mesto i dlya smesheniya $s_{2}$ vtoroi massy. Esli proanalizirovat' otnoshenie amplitud $s_{02} / s_{01}$ v zavisimosti ot chastoty $\omega ,$ to okazyvaetsya, chto eto otnoshenie vblizi chastoty $\omega _{I}$ ravno koefficientu raspredeleniya amplitud $\varsigma _{I}$ dlya pervoi mody, a vblizi chastoty $\omega _{II}$ - koefficientu raspredeleniya amplitud $\varsigma _{II}$ dlya vtoroi mody. Eto ispol'zuetsya dlya opredeleniya etih koefficientov, poskol'ku pri vynuzhdennyh kolebaniyah eto sdelat' proshe, chem pri sobstvennyh.

Nazad| Vpered

Publikacii s klyuchevymi slovami: kolebaniya - volny Publikacii so slovami: kolebaniya - volny
Sm. takzhe: Eho iz glubin krasnogo giganta

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

Kolebaniya i volny. Lekcii.

Zatuhanie kolebanii.

Energiya kolebatel'noi sistemy i ee dissipaciya.

Vynuzhdennye kolebaniya.