Astronet > Kolebaniya i volny

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Kolebaniya i volny. Lekcii.

V.A.Aleshkevich, L.G.Dedenko, V.A.Karavaev (Fizicheskii fakul'tet MGU)
Izdatel'stvo Fizicheskogo fakul'teta MGU, 2001 g. Soderzhanie

Kolebaniya sistem so mnogimi stepenyami svobody.

Osnovnye idei, sformulirovannye pri rassmotrenii kolebanii sistem s dvumya stepenyami svobody, teper' mogut byt' s uspehom ispol'zovany dlya analiza kolebanii sistem s tremya, chetyr'mya, $\ldots, N$ stepenyami svobody, i v predele, pri $N \to \infty ,$ dlya analiza kolebanii v sploshnyh sredah, t.e. voln.

Obratimsya vnachale k kolebaniyam treh odinakovyh mass $m,$ zakreplennyh na ravnyh rasstoyaniyah $a$ na natyanutom legkom rezinovom shnure, kak pokazano na ris. 3.13a. Lyuboe kolebanie etoi sistemy mozhet byt' predstavleno kak superpoziciya treh normal'nyh kolebanii s chastotami $\omega _{I} , \omega _{II}$ i $\omega _{III} .$ Opuskaya na vremya vopros o velichine chastot, naidem konfiguraciyu etih mod. Primem vo vnimanie, chto kvadrat chastoty kolebanii kazhdoi massy v dannoi mode dolzhen byt' odinakov. Etogo mozhno dobit'sya v sluchae, kogda otnosheniya vozvrashayushei sily k velichine massy $m$ i ee smesheniyu $s$ u vseh gruzov budut odinakovymi. Takie usloviya realizuyutsya pri smeshenii mass tremya sposobami (b, v i g na ris. 3.13). Pri otpuskanii gruzov iz polozheniya (b) v sisteme budet proishodit' pervoe normal'noe kolebanie na chastote $\omega _{I}$ ; iz polozheniya (v) - vtoroe na chastote $\omega _{II}$ ; iz polozheniya (g) - tret'e na chastote $\omega _{III} .$ Ochevidno, chto $\omega _{III} \gt \omega _{II} \gt \omega _{I} .$

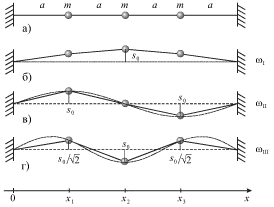Ris. 3.13.

Konfiguraciya kazhdoi iz mod mozhet byt' opisana s pomosh'yu dvuh koefficientov raspredeleniya amplitud. Zabegaya vpered, otmetim, chto dlya chetyreh mass takih koefficientov dolzhno byt' tri, i t.d.

Odnako situaciya mozhet byt' uproshena, esli obratit' vnimanie, chto raspolozhenie mass v poziciyah (b), (v) i (g) na ris. 3.13 napominaet "sinusoidal'noe" (punktirom izobrazhen fragment funkcii $\sin kx,$ gde $k$ - nekotoryi parametr, harakterizuyushii period etoi funkcii). Togda konfiguraciya pervoi mody budet opisana sleduyushim obrazom:

(3.44a)

$s_{0}^{I} (x) = s_{0} \sin k_{I} x; \quad k_{I} = {\displaystyle \frac{\displaystyle {\displaystyle \pi }}{\displaystyle {\displaystyle 4a}}}.$

Dlya vtoroi mody:

(3.44b)

$s_{0}^{II} (x) = s_{0} \sin k_{II} x; \quad k_{II} = 2k_{I} .$

Dlya tret'ei mody:

(3.44v)

$s_{0}^{III} (x) = s_{0} \sin k_{III} x; \quad k_{III} = 3k_{I} .$

Rol' bezrazmernyh koefficientov $\varsigma$ vypolnyaet funkciya $\sin k_{p} x (p = I, II, III),$ vychislennaya v tochkah $x = x_{1} = a, x = x_{2} = 2a, x = x_{3} = 3a.$

Drugimi primerami svyazannyh oscillyatorov yavlyayutsya atomy v molekulah CO₂, H₂O i t. d. Na ris. 3.14 izobrazheny konfiguracii mod i privedeny znacheniya chastot normal'nyh kolebanii molekul. Obratim vnimanie, chto eti chastoty imeyut poryadok velichiny $(10^{13}\div 10^{14})$ s^-1 i znachitel'no prevyshayut (na neskol'ko poryadkov) chastoty mehanicheskih kolebanii makroskopicheskih sistem. Rezonansnye kolebaniya etih (i drugih) molekul mozhno vozbudit' pri vzaimodeistvii raznoimenno zaryazhennyh ionov, sostavlyayushih eti molekuly, s elektricheskim polem svetovoi elektromagnitnoi volny infrakrasnogo (IK) diapazona, imeyushei blizkuyu chastotu.

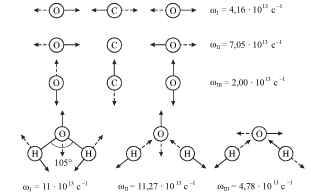Ris. 3.14.

V kurse "Optika" my poznakomimsya s takim vzaimodeistviem, privodyashim, v chastnosti, k oslableniyu (poglosheniyu) energii svetovoi volny i ee rasseyaniyu v srede s koleblyushimisya molekulami (kombinacionnomu rasseyaniyu).

Budem uvelichivat' chislo mass, zakreplennyh na shnure cherez ravnye promezhutki a. Esli $N$ - chislo etih mass, to polnaya dlina shnura ravna $\ell = a(N + 1)$ (ris. 3.15). Rasschitaem normal'nye chastoty vseh mod i ih konfiguracii. Budem schitat', chto nevesomyi shnur natyanut s siloi $F,$ i pri malyh otkloneniyah mass ot polozheniya ravnovesiya $s \ll \ell$ eta sila ne menyaetsya. Kazhdaya massa ispytyvaet deistvie sil natyazheniya shnura po obe storony ot nee.

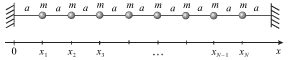Ris. 3.15.

Na ris. 3.16 pokazano mgnovennoe polozhenie fragmenta shnura i treh mass. Esli ugly $\theta _{1}$ i $\theta _{2}$ maly, to vozvrashayushaya sila, deistvuyushaya na srednyuyu massu, ravna:

(3.45)

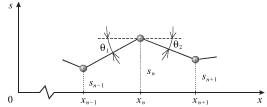$f = - F \cdot (\sin \theta _{1} + \sin \theta _{2} ) \approx - F(\theta _{1} + \theta _{2} ).$

Ris. 3.16.

Velichiny uglov $\theta _{1}$ i $\theta _{2}$ opredelyayutsya vzaimnym raspolozheniem mass:

(3.46)

$\theta _{1} \approx {\displaystyle \frac{\displaystyle {\displaystyle s_{n} - s_{n - 1} }}{\displaystyle {\displaystyle a}}}; \quad \theta _{2} \approx {\displaystyle \frac{\displaystyle {\displaystyle s_{n} - s_{n + 1} }}{\displaystyle {\displaystyle a}}}.$

S uchetom (3.45) i (3.46) uravnenie dvizheniya srednei massy primet vid:

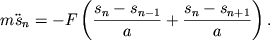(3.47)

$m\ddot {\displaystyle s}_{n} = - F\left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle s_{n} - s_{n - 1} }}{\displaystyle {\displaystyle a}}} + {\displaystyle \frac{\displaystyle {\displaystyle s_{n} - s_{n + 1} }}{\displaystyle {\displaystyle a}}}} \right).$

Esli kolebaniya yavlyayutsya normal'nymi, to

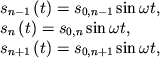(3.48)

$\begin{array}{l} s_{n - 1} \left( {\displaystyle t} \right) = s_{0,n - 1} \sin \omega t, \\ s_{n} \left( {\displaystyle t} \right) = s_{0,n} \sin \omega t, \\ s_{n + 1} \left( {\displaystyle t} \right) = s_{0,n + 1} \sin \omega t, \\ \end{array}$

gde chastotu $\omega$ i raspredelenie amplitud predstoit opredelit'.

Podstavlyaya (3.48) v (3.47), poluchim

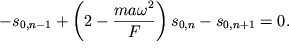(3.49)

$- s_{0,n - 1} + \left( {\displaystyle 2 - {\displaystyle \frac{\displaystyle {\displaystyle ma\omega ^{2}}}{\displaystyle {\displaystyle F}}}} \right)s_{0,n} - s_{0,n + 1} = 0.$

Poskol'ku $n = 1, 2, 3, \ldots, N,$ to (3.49) predstavlyaet soboi sistemu $N$ lineinyh odnorodnyh uravnenii. Iz usloviya ravenstva nulyu ee opredelitelya mozhno rasschitat' vse $N$ normal'nyh chastot, a zatem dlya kazhdoi iz etih chastot opredelit' raspredelenie amplitud v kazhdoi mode, chislo kotoryh, ochevidno, budet ravno $N.$

My zhe ispol'zuem uzhe opisannyi ranee bolee legkii put' i budem iskat' konfiguraciyu kazhdoi mody v vide "sinusoidal'noi" konfiguracii:

(3.50)

$s_{0} (x) = s_{0} \sin kx,ili \quad s_{0n} = s_{0} (x_{n} ),$

gde $x_{1} = a, x_{2} = 2a,\ldots,x_{n} = na,\ldots,x_{N} = Na.$

Ubedimsya, chto konfiguraciya (3.50) udovletvoryaet uravneniyu (3.49), kotoroe perepishem v vide:

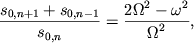(3.51)

${\displaystyle \frac{\displaystyle {\displaystyle s_{0,n + 1} + s_{0,n - 1} }}{\displaystyle {\displaystyle s_{0,n} }}} = {\displaystyle \frac{\displaystyle {\displaystyle 2\Omega ^{2} - \omega ^{2}}}{\displaystyle {\displaystyle \Omega ^{2}}}},$

gde $\Omega ^{2} = {\displaystyle \frac{\displaystyle {\displaystyle F}}{\displaystyle {\displaystyle ma}}}.$

Podstavim (3.50) v levuyu chast' (3.51):

(3.52)

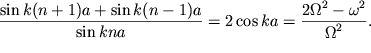${\displaystyle \frac{\displaystyle {\displaystyle \sin k(n + 1)a + \sin k(n - 1)a}}{\displaystyle {\displaystyle \sin kna}}} = 2\cos ka = {\displaystyle \frac{\displaystyle {\displaystyle 2\Omega ^{2} - \omega ^{2}}}{\displaystyle {\displaystyle \Omega ^{2}}}}.$

Ochevidno, chto (3.50) udovletvorit uravneniyu (3.49), esli podobrat' dlya dannogo $k$ podhodyashuyu chastotu $\omega .$

Parametr $k$ nazovem volnovym chislom. Ob'yasnenie etomu budet dano v posleduyushih lekciyah. Etot parametr dolzhen byt' takim, chtoby na koncah zakreplennogo shnura udovletvoryalis' granichnye usloviya. Pri $x = 0$ eti usloviya vypolnyayutsya: $\sin (k \cdot 0) = 0.$ Na drugom konce, gde $x = a(N + 1),$ potrebuem, chtoby

(3.53)

$\sin ka(N + 1) = 0,$

otkuda poluchaem:

(3.54)

$k_{p} a(N + 1) = p \cdot \pi ,ili \quad k_{p} = {\displaystyle \frac{\displaystyle {\displaystyle p\pi }}{\displaystyle {\displaystyle a(N + 1)}}},$

gde celoe chislo $p = I, II, \ldots, N$ harakterizuet nomer mody (kolichestvo mod, kak bylo pokazano vyshe, ravno $N$ ). Kazhdoi p-oi mode sootvetstvuet svoya chastota, kotoraya legko nahoditsya iz uravneniya (3.52):

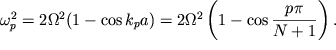(3.55)

$\omega _{p}^{2} = 2\Omega ^{2}(1 - \cos k_{p} a) = 2\Omega ^{2}\left( {\displaystyle 1 - \cos {\displaystyle \frac{\displaystyle {\displaystyle p\pi }}{\displaystyle {\displaystyle N + 1}}}} \right).$

Znaya volnovye chisla $k_{p}$ i normal'nye chastoty $\omega _{p} ,$ ne sostavlyaet truda zapisat' vyrazheniya dlya smeshenii vseh mass, kak funkcii vremeni. Dlya r-oi mody mozhno zapisat':

(3.56)

$s_{p} (x_{n} ,t) = s_{0p} \sin k_{p} x_{n} \cdot \sin (\omega _{p} t + \varphi _{p} );$

zdes' $x_{n} = na; n = 1, 2, \ldots, N.$

Amplituda $s_{0p}$ i nachal'naya faza $\varphi _{p}$ opredelyayutsya nachal'nymi usloviyami, a $k_{p}$ i $\omega _{p}$ - svoistvami samoi sistemy (formuly 3.54 i 3.55).

V silu lineinosti kolebatel'noi sistemy v samom obshem sluchae kolebanii poluchaem dlya smesheniya vseh chastic vyrazhenie:

(3.57)

$s(x_{n} ,t) = {\displaystyle \sum\limits_{p} {\displaystyle s_{p} \left( {\displaystyle x_{n} ,t} \right),} }$

gde summirovanie provoditsya tol'ko po tem modam, kotorye "uchastvuyut" v kolebaniyah.

Tak, naprimer, uderzhivaya vse vremya srednyuyu massu v polozhenii ravnovesiya, my ne mozhem vozbudit' mody s nechetnymi nomerami $p = I, III, \ldots,$ poskol'ku eti mody "trebuyut" smesheniya central'noi massy.

Pol'zuyas' formuloi (3.55), netrudno vychislit' normal'nye chastoty koleblyushihsya mass na shnure.

Na ris. 3.17 izobrazheny mody kolebanii v sisteme s odnoi, dvumya i tremya massami i dlya kazhdoi mody ukazany velichiny normal'nyh chastot.

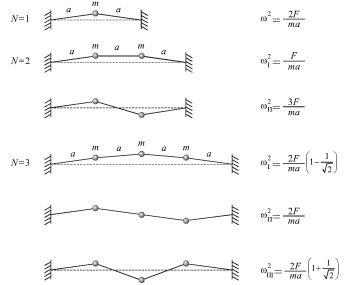Ris. 3.17.

V zaklyuchenie otmetim, chto svyaz' tipa (3.55) mezhdu chastotoi $\omega$ i volnovym chislom $k$ nazyvaetsya dispersionnym sootnosheniem. Eto sootnoshenie budet dalee ispol'zovano pri analize rasprostraneniya voln v periodicheskih strukturah.

Nazad| Vpered

Publikacii s klyuchevymi slovami: kolebaniya - volny Publikacii so slovami: kolebaniya - volny
Sm. takzhe: Eho iz glubin krasnogo giganta

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce