Astronet > Kolebaniya i volny

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Kolebaniya i volny. Lekcii.

V.A.Aleshkevich, L.G.Dedenko, V.A.Karavaev (Fizicheskii fakul'tet MGU)
Izdatel'stvo Fizicheskogo fakul'teta MGU, 2001 g. Soderzhanie

Rasprostranenie vozmushenii v sisteme s bol'shim chislom stepenei svobody. Skorost' rasprostraneniya. Vozbuzhdenie voln. Gruppa voln i ee skorost'. Volnovoe uravnenie. Volny v sploshnom shnure. Otrazhenie voln. Vozbuzhdenie stoyachih voln v shnure. Mody kolebanii. Volny v uprugih telah. Poperechnye volny. Energiya, perenosimaya volnoi. Vektor Umova. Prodol'nye volny. Skorost' voln v tonkom i tolstom sterzhnyah. Otrazhenie i prohozhdenie voln na granicah dvuh sred. Udel'noe volnovoe soprotivlenie.

Rasprostranenie vozmushenii v sisteme s bol'shim chislom stepenei svobody.

Rassmotrim kolebaniya $N \gg 1$ mass na rezinovom shnure (ris. 4.1a). Otklonim neskol'ko mass v seredine shnura ot polozheniya ravnovesiya (ris 4.1b), i zatem otpustim ih v moment vremeni $t = 0.$ Kak pokazyvaet opyt, eta nachal'naya konfiguraciya, predstavlyayushaya soboi po forme impul's, s techeniem vremeni transformiruetsya v dva odinakovyh impul'sa, kotorye pobegut v raznye storony s nekotoroi konechnoi skorost'yu c (ris. 4.1v). Eti impul'sy dobegut do koncov shnura, izmenyat svoyu polyarnost' pri otrazhenii i pobegut v obratnom napravlenii (ris. 4.1g). Posle vstrechi v seredine shnura oni otrazyatsya eshe raz, vosstanovyat ishodnuyu polyarnost' i spustya vremya $\Delta t = 2\ell / c$ vnov' vstretyatsya v seredine, sformirovav ishodnyi impul's. Zatem etot process s periodom $\Delta t$ budet povtoryat'sya do teh por, poka impul'sy ne zatuhnut iz-za dissipacii energii.

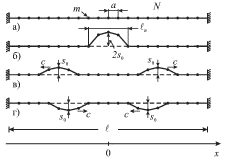Ris. 4.1.

S tochki zreniya povsednevnogo opyta v etom net nichego udivitel'nogo, poskol'ku smesheniya gruppy mass vedut k vozniknoveniyu uprugih sil, stremyashihsya vernut' etu gruppu v polozhenie ravnovesiya i odnovremenno vyvesti sosednie chasticy iz polozheniya ravnovesiya.

S tochki zreniya opisaniya kolebanii "na yazyke mod" takzhe ponyatno, chto otkloniv, a zatem otpustiv gruppu chastic, my vozbuzhdaem mnogo mod. Kolebaniya vseh $N$ chastic proishodyat odnovremenno na neskol'kih normal'nyh chastotah $\omega _{p}.$ Vse eti chastoty razlichny, i summa normal'nyh kolebanii predstavlyaet soboi bieniya. Poskol'ku cherez vremya, ravnoe periodu bienii, kolebaniya gruppy chastic v centre shnura vosstanovyatsya, to ochevidno, chto period bienii raven upominavshemusya neskol'ko ranee vremeni $\Delta t = 2\ell / c.$

Opredelim skorost' s, ishodya iz predstavleniya o bieniyah, kak superpozicii normal'nyh kolebanii. Dlya etogo vnachale perepishem dispersionnoe sootnoshenie (3.55) v vide

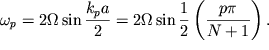$\omega _{p} = 2\Omega \sin {\displaystyle \frac{\displaystyle {\displaystyle k_{p} a}}{\displaystyle {\displaystyle 2}}} = 2\Omega \sin {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}\left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle p\pi }}{\displaystyle {\displaystyle N + 1}}}} \right).$

(4.1)

Strogo govorya, pri nalichii mnogih chastot v spektre kolebanii, davaemyh formuloi (4.1), bieniya ne budut periodicheskimi - nachal'naya konfiguraciya ne povtoryaetsya. Vizual'no eto budet proyavlyat'sya v iskazhenii formy begushih impul'sov, esli dlina impul'sa $\ell _{i} \geq a$ (impul's "nakryvaet" malo chastic), a shnur dostatochno dlinnyi. Govoryat, chto iskazhenie impul'sa svyazano s dispersiei "sredy" (shnura s massami), po kotoroi impul's rasprostranyaetsya.

Eto iskazhenie budet nichtozhnym, esli $\ell _{i} \gg a$ (gruppa sostoit iz bol'shogo chisla koleblyushihsya mass). Tak obychno i proishodit pri rasprostranenii vozmushenii v tverdom tele, gde $a\sim 10^{ - 10} m$ (rasstoyanie mezhdu uzlami kristallicheskoi reshetki, okolo kotoryh koleblyutsya atomy).

Esli $\ell _{i} \gg a,$ to v spektre kolebanii dominiruyut nizshie mody, kotorye harakterizuyutsya volnovymi chislami $k_{p},$ gde $p = I, II, III, \ldots \ll N.$ Chastoty etih mod poluchayutsya iz formuly (4.1):

$\omega _{p} = \Omega ak_{p} = {\displaystyle \frac{\displaystyle {\displaystyle \Omega \pi }}{\displaystyle {\displaystyle N + 1}}} \cdot p; p = I, II, III, \ldots$

(4.2)

Zdes' ispol'zovano priblizhenie $\sin x \approx x$ pri $x \ll 1.$ Eta zavisimost' $\omega _{p} (k_{p} )$ izobrazhena na ris. 4.2.

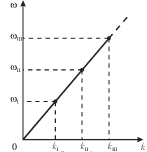Ris. 4.2.

Obratim vnimanie, chto nizshie chastoty raspolagayutsya ekvidistantno: $\Delta \omega = \omega _{II} - \omega _{I} = \omega _{III} - \omega _{II} = \ldots$ Poetomu period bienii (sm. takzhe formulu (3.14)) poluchaetsya ravnym:

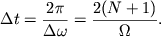$\Delta t = {\displaystyle \frac{\displaystyle {\displaystyle 2\pi }}{\displaystyle {\displaystyle \Delta \omega }}} = {\displaystyle \frac{\displaystyle {\displaystyle 2(N + 1)}}{\displaystyle {\displaystyle \Omega }}}.$

(4.3)

Esli uchest', chto dlina shnura $\ell = a\left( {\displaystyle N + 1} \right),$ to skorost' dvizheniya impul'sa v srede bez dispersii ravna:

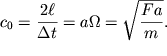$c_{0} = {\displaystyle \frac{\displaystyle {\displaystyle 2\ell }}{\displaystyle {\displaystyle \Delta t}}} = a\Omega = \sqrt {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle Fa}}{\displaystyle {\displaystyle m}}}}.$

(4.4)

Esli my budem uvelichivat' chislo mass $N$ na shnure fiksirovannoi dliny, tem samym umen'shaya rasstoyanie $a,$ to my sdelaem predel'nyi perehod k nepreryvnomu raspredeleniyu mass - t.e. k odnorodnomu vesomomu shnuru, pri etom

$\rho _{1} = m / a$

(4.5)

yavlyaetsya massoi edinicy dliny odnorodnogo shnura (inogda upotreblyayut termin "plotnost' edinicy dliny"). Poetomu okonchatel'no dlya skorosti rasprostraneniya impul'sa proizvol'noi formy po shnuru imeem

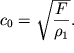$c_{0} = \sqrt {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle F}}{\displaystyle {\displaystyle \rho _{1} }}}}.$

(4.6)

Naprimer, v sluchae tonkogo rezinovogo shlanga s lineinoi plotnost'yu $\rho _{1} \sim 0,1 kg/m,$ natyanutogo s siloi $F\sim 10^{2} N,$ skorost' dvizheniya impul'sa poluchaetsya ravnoi $c_{0} \sim 30 m/s.$ Takaya sravnitel'no nebol'shaya velichina skorosti pozvolyaet legko nablyudat' rasprostranenie i otrazhenie impul'sa.

Itak, podvedem nekotorye itogi.

1. Esli prenebrech' periodicheskoi strukturoi sredy, to skorost' $c_{0}$ rasprostraneniya impul'sa ne zavisit ot ego formy, a sam impul's pri rasprostranenii ne iskazhaetsya (net dispersii).

2. Esli os' x napravit' vdol' shnura i zadat' nachal'noe vozmushenie (v moment $t = 0$ ) v vide $s(x),$ to s techeniem vremeni vozmushenie shnura budet imet' vid:

${\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}s(x - c_{0} t) + {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}s(x + c_{0} t).$

(4.7)

Pervoe slagaemoe opisyvaet vozmushenie, begushee so skorost'yu $c_{0}$ v polozhitel'nom napravlenii osi h, ukazannom na ris. 4.1, a vtoroe sootvetstvuet impul'su, rasprostranyayushemusya v protivopolozhnom napravlenii.

3. U koncov nevesomogo shnura s massami oba impul'sa otrazhayutsya. Otrazhennyi impul's imeet protivopolozhnuyu polyarnost' (napravlenie smesheniya $s$ ) po sravneniyu s padayushim.

Analogichnye granichnye usloviya realizuyutsya dlya sploshnogo massivnogo shnura s zakreplennymi koncami (ris. 4.3).

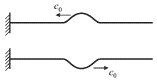Ris. 4.3.

4. V oblasti perekrytiya begushih impul'sov obrazuetsya kolebanie, nazyvaemoe stoyachei volnoi. Tak my prihodim k ponyatiyam begushih i stoyachih voln, pri etom stoyachaya volna mozhet rassmatrivat'sya kak superpoziciya voln, begushih v protivopolozhnyh napravleniyah.

Vozbuzhdenie voln.

Rassmotrim kolebaniya nevesomogo shnura s gruzami, pravyi konec kotorogo zakreplen, a levyi pod deistviem vneshnei sily v moment vremeni $t = 0$ nachinaet smeshat'sya po garmonicheskomu zakonu:

$s(t) = s_{0} \sin \omega t.$

(4.8)

Pod deistviem etoi sily gruzy, svyazannye drug s drugom otrezkami natyanutogo shnura, rano ili pozdno nachnut sovershat' vynuzhdennye garmonicheskie kolebaniya s chastotoi $\omega.$ Estestvenno, chto sistemu gruzov (po analogii s sistemoi s dvumya gruzami) mozhno zametno raskachat' lish' v sluchae rezonansa, kogda chastota $\omega$ sovpadaet s odnoi iz normal'nyh chastot $\omega _{p}.$

Vnachale pridut v dvizhenie gruzy vblizi levogo podvizhnogo konca shnura, a s techeniem vremeni v kolebaniya budut vovlekat'sya vse novye gruzy.

Takie kolebaniya predstavlyayut soboi volnovoi process (volnu), rasprostranyayushiisya "sleva - napravo" s nekotoroi skorost'yu $c_{p}.$ Na ris. 4.4 izobrazheny polozheniya koleblyushihsya mass v nekotoryi moment vremeni $t_{0}.$ Poskol'ku gruzy koleblyutsya "poperek" napravleniya rasprostraneniya (osi Oh), to volna nazyvaetsya poperechnoi. Eta volna dobezhit do pravogo zakreplennogo konca shnura i otrazitsya. Posle etogo budut sushestvovat' dve volny: ishodnaya begushaya (inogda ee nazyvayut padayushei volnoi) i otrazhennaya volna, kotoraya bezhit navstrechu padayushei. Spustya vremya $\Delta t = 2\ell / c_{p}$ otrazhennaya volna dostignet levogo konca, snova otrazitsya, i "sformiruetsya" moda kolebanii. Konfiguraciya etoi mody zadaetsya volnovym chislom $k_{p}$ (sm. sootnoshenie (4.1)).

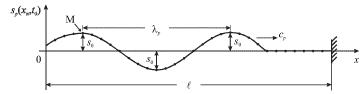Ris. 4.4.

Rassmotrim podrobnee padayushuyu volnu s etim $k_{p}.$ Prostranstvennyi period $\lambda _{p},$ izobrazhennyi na ris. 4.4 kak minimal'noe rasstoyanie mezhdu massami, koleblyushimisya v faze, nazyvaetsya dlinoi volny. Dlina volny svyazana s volnovym chislom $k_{p}$ sootnosheniem:

$k_{p} = 2\pi / \lambda _{p}.$

(4.9)

Esli sily vyazkogo treniya, prilozhennye k kazhdomu iz gruzov, maly, to amplitudy kolebanii vseh gruzov budut odinakovy i ravny $s_{0}.$ Teper' my mozhem zapisat' uravnenie begushei volny - uravnenie, opisyvayushee smeshenie lyuboi iz mass v proizvol'nyi moment vremeni. Dlya chastoty $\omega _{p},$ volnovogo chisla $k_{p}$ i amplitudy $s_{0}$ ono imeet vid:

$\begin{array}{l} s_{p} (x_{n},t) = s_{0} \sin (\omega _{p} t - k_{p} x_{n} ); \\ x_{n} = a; 2a; \ldots; na; \ldots; Na. \\ \end{array}$

(4.10)

Vyrazhenie $\varphi = \omega _{p} t - k_{p} x_{n}$ nazyvaetsya fazoi volny. Uravnenie (4.10) otrazhaet tot fakt, chto vse massy koleblyutsya s odinakovoi chastotoi $\omega _{p},$ imeyut odinakovuyu amplitudu $s_{0},$ odnako eti kolebaniya razlichayutsya po faze $\varphi.$

Nazad| Vpered

Publikacii s klyuchevymi slovami: kolebaniya - volny Publikacii so slovami: kolebaniya - volny
Sm. takzhe: Eho iz glubin krasnogo giganta

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

Kolebaniya i volny. Lekcii.

Lekciya 4

Rasprostranenie vozmushenii v sisteme s bol'shim chislom stepenei svobody.

Vozbuzhdenie voln.