Astronet > Kolebaniya i volny

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Kolebaniya i volny. Lekcii.

V.A.Aleshkevich, L.G.Dedenko, V.A.Karavaev (Fizicheskii fakul'tet MGU)
Izdatel'stvo Fizicheskogo fakul'teta MGU, 2001 g. Soderzhanie

Nezatuhayushie garmonicheskie kolebaniya sistem s odnoi stepen'yu svobody.

Esli polozhenie sistemy mozhet byt' opisano odnim edinstvennym parametrom $f(t)$ , zavisyashim ot vremeni, to takaya sistema imeet odnu stepen' svobody. Primerami takih sistem yavlyayutsya horosho izvestnye iz shkol'nogo kursa matematicheskii i pruzhinnyi mayatniki, izobrazhennye na ris. 1.1, esli pervyi iz nih dvizhetsya v odnoi ploskosti, a vtoroi - po pryamoi.

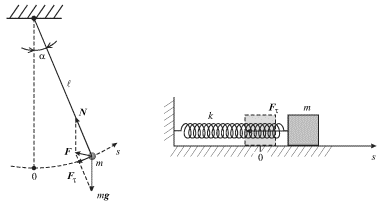Ris. 1.1.

Dlya matematicheskogo mayatnika $f(t)$ mozhet harakterizovat' libo uglovoe smeshenie $(f(t) = \alpha (t))$ , libo lineinoe smeshenie vdol' traektorii $(f(t) = s(t))$ tochechnoi massy $m$ ot polozheniya ravnovesiya, a dlya pruzhinnogo mayatnika $f(t) = s(t),$ gde $s(t)$ - smeshenie massy m ot ee ravnovesnogo polozheniya, izobrazhennogo punktirom.

Dvizhenie takih i podobnyh im sistem mozhno opisat' na osnove vtorogo zakona N'yutona:

$m{\displaystyle \bf a} = {\displaystyle \bf F}$

(1.1)

Esli prenebrech' vnachale silami soprotivleniya (v dal'neishem my uchtem ih deistvie), to na massu $m$ matematicheskogo mayatnika budet deistvovat' rezul'tiruyushaya sila $\bf F} = {\displaystyle \bf N} + m{\displaystyle \bf g$ ( $\bf N$ - sila natyazheniya niti), napravlennaya, voobshe govorya, pod uglom k traektorii, a na massu $m$ pruzhinnogo mayatnika, lezhashego na gladkoi gorizontal'noi poverhnosti, - gorizontal'naya sila $\bf F}_{\tau$ , yavlyayushayasya funkciei smesheniya $s$ ot polozheniya ravnovesiya.

Tak kak smeshenie $s(t)$ v sluchae matematicheskogo mayatnika opredelyaetsya tangencial'nym uskoreniem, to uravnenie (1.1) dlya oboih mayatnikov zapishetsya v vide

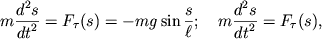$m{\displaystyle \frac{\displaystyle {\displaystyle d^{2}s}}{\displaystyle {\displaystyle dt^{2}}}} = F_{\tau } (s) = - mg \sin {\displaystyle \frac{\displaystyle {\displaystyle s}}{\displaystyle {\displaystyle \ell }}}; \quad m{\displaystyle \frac{\displaystyle {\displaystyle d^{2}s}}{\displaystyle {\displaystyle dt^{2}}}} = F_{\tau } (s),$

(1.2)

gde $\ell$ - dlina niti.

V pervom uravnenii ispol'zovana proekciya $F_{\tau } (s)$ rezul'tiruyushei sily $\bf F$ na napravlenie skorosti v vide $F_{\tau } = - mg \sin \alpha = - mg \sin {\displaystyle \frac{\displaystyle {\displaystyle s}}{\displaystyle {\displaystyle \ell }}}.$

V rassmatrivaemyh primerah vozvrashayushaya sila $F_{\tau } (s)$ yavlyaetsya, voobshe govorya, nelineinoi funkciei smesheniya $s$ . Poetomu tochnoe reshenie uravnenii (1.2), kotorye yavlyayutsya nelineinymi, poluchit' ne udaetsya. Dalee my rassmotrim nekotorye primery takih nelineinyh kolebanii.

Zdes' zhe my budem schitat' smesheniya malymi po sravneniyu s dlinoi niti ili dlinoi nedeformirovannoi pruzhiny. Pri takih predpolozheniyah vozvrashayushaya sila proporcional'na smesheniyu:

$F_{\tau } (s) = - mg{\displaystyle \frac{\displaystyle {\displaystyle s}}{\displaystyle {\displaystyle \ell }}}; \quad F_{\tau } (s) = - ks .$

(1.3)

Vyrazhenie sleva zapisano pri uchete usloviya $\sin {\displaystyle \frac{\displaystyle {\displaystyle s}}{\displaystyle {\displaystyle \ell }}} \approx {\displaystyle \frac{\displaystyle {\displaystyle s}}{\displaystyle {\displaystyle \ell }}},$ a sprava - s ispol'zovaniem zakona Guka, spravedlivogo pri malyh deformaciyah pruzhiny s zhestkost'yu $k$ .

S uchetom (1.3) uravneniya (1.2) primut odinakovyi vid:

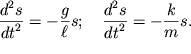${\displaystyle \frac{\displaystyle {\displaystyle d^{2}s}}{\displaystyle {\displaystyle dt^{2}}}} = - {\displaystyle \frac{\displaystyle {\displaystyle g}}{\displaystyle {\displaystyle \ell }}}s; \quad {\displaystyle \frac{\displaystyle {\displaystyle d^{2}s}}{\displaystyle {\displaystyle dt^{2}}}} = - {\displaystyle \frac{\displaystyle {\displaystyle k}}{\displaystyle {\displaystyle m}}}s.$

(1.4)

Razlichayutsya lish' koefficienty v pravyh chastyah etih uravnenii, kotorye chislenno ravny otnosheniyu vozvrashayushei sily pri edinichnom smeshenii k masse koleblyushegosya tela i imeyut razmernost' [s^-2]. Esli ispol'zovat' oboznacheniya

$\omega _{0}^{2} = {\displaystyle \frac{\displaystyle {\displaystyle g}}{\displaystyle {\displaystyle \ell }}}, \quad \omega _{0}^{2} = {\displaystyle \frac{\displaystyle {\displaystyle k}}{\displaystyle {\displaystyle m}}},$

(1.5)

to uravneniya (1.4) primut vid uravneniya nezatuhayushih garmonicheskih kolebanii, ili uravneniya garmonicheskogo oscillyatora:

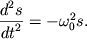${\displaystyle \frac{\displaystyle {\displaystyle d^{2}s}}{\displaystyle {\displaystyle dt^{2}}}} = - \omega _{0}^{2} s.$

(1.6)

Resheniem uravneniya (1.6) yavlyaetsya semeistvo garmonicheskih funkcii

$s(t) = s_{0} \sin (\omega _{0} t + \varphi _{0} ),$

(1.7)

v chem legko ubedit'sya, dvazhdy prodifferencirovav funkciyu $s(t)$ po vremeni:

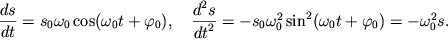${\displaystyle \frac{\displaystyle {\displaystyle ds}}{\displaystyle {\displaystyle dt}}} = s_{0} \omega _{0} \cos (\omega _{0} t + \varphi _{0} ), \quad {\displaystyle \frac{\displaystyle {\displaystyle d^{2}s}}{\displaystyle {\displaystyle dt^{2}}}} = - s_{0} \omega _{0}^{2} \sin ^{2}(\omega _{0} t + \varphi _{0} ) = - \omega _{0}^{2} s.$

Zametim, chto esli uravnenie dvizheniya privoditsya k vidu (1.6), to ego resheniem yavlyayutsya garmonicheskie funkcii (1.7) s chastotoi $\omega _{0},$ ravnoi kornyu kvadratnomu iz koefficienta pri $s$ .

Znacheniya etih garmonicheskih funkcii v nachal'nyi moment vremeni (pri $t = 0$ ) opredelyayutsya nachal'noi fazoi $\varphi _{0}$ (sm. nizhe) i amplitudoi kolebanii $s_{0} .$ U odnoi i toi zhe sistemy eti znacheniya mogut byt' razlichnymi pri raznyh sposobah vozbuzhdeniya kolebanii.

Chtoby vozbudit' sobstvennye kolebaniya, nado vnachale (pri $t = 0$ ) libo otklonit' telo (zadat' nachal'noe smeshenie $s(0)$ ), libo tolknut' ego (zadat' nachal'nuyu skorost' ${\displaystyle \frac{\displaystyle {\displaystyle ds}}{\displaystyle {\displaystyle dt}}}(0) = v(0)$ ), libo sdelat' i to, i drugoe odnovremenno. Znanie nachal'nyh uslovii (smesheniya i skorosti) pozvolyaet opredelit' amplitudu $s_{0}$ i nachal'nuyu fazu kolebanii $\varphi _{0}$ iz ochevidnyh uravnenii:

$s(0) = {\displaystyle \left. {\displaystyle s(t)} \right|}_{t = 0} = {\displaystyle \left. {\displaystyle s_{0} \sin (\omega _{0} t + \varphi _{0} )} \right|}_{t = 0} = s_{0} \sin \varphi _{0} ;$

(1.8)

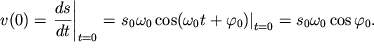$v(0) = {\displaystyle \left. {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle ds}}{\displaystyle {\displaystyle dt}}}} \right|}_{t = 0} = {\displaystyle \left. {\displaystyle s_{0} \omega _{0} \cos (\omega _{0} t + \varphi _{0} )} \right|}_{t = 0} = s_{0} \omega _{0} \cos \varphi _{0} .$

(1.9)

Reshenie etih uravnenii imeet vid:

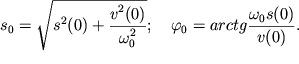$s_{0} = \sqrt {\displaystyle s^{2}(0) + {\displaystyle \frac{\displaystyle {\displaystyle v^{2}(0)}}{\displaystyle {\displaystyle \omega _{0}^{2} }}}} ; \quad \varphi _{0} = arctg{\displaystyle \frac{\displaystyle {\displaystyle \omega _{0} s(0)}}{\displaystyle {\displaystyle v(0)}}}.$

(1.10)

Vazhno otmetit', chto amplituda kolebanii $s_{0},$ ravnaya velichine maksimal'nogo smesheniya tela ot polozheniya ravnovesiya, mozhet prevoshodit' nachal'noe smeshenie $s(0)$ pri nalichii nachal'nogo tolchka.

Naryadu s krugovoi chastotoi $\omega _{0}$ kolebaniya harakterizuyutsya ciklicheskoi chastotoi $\nu _{0} = \omega _{0} / 2\pi ,$ ravnoi chislu kolebanii za edinicu vremeni, i periodom kolebanii $T = 1 / \nu _{0},$ ravnym dlitel'nosti odnogo kolebaniya.

Period garmonicheskih kolebanii (ravno kak i chastoty $\omega _{0}$ i $\nu _{0}$ ) ne zavisit ot nachal'nyh uslovii i raven

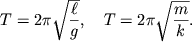$T = 2\pi \sqrt {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \ell }}{\displaystyle {\displaystyle g}}}}, \quad T = 2\pi \sqrt {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle m}}{\displaystyle {\displaystyle k}}}} .$

(1.11)

Drugim primerom yavlyayutsya kolebaniya fizicheskogo mayatnika - tela proizvol'noi formy massy $m$ , zakreplennogo na gorizontal'noi osi {\displaystyle O}' tak, chto ego centr mass nahoditsya v tochke O, udalennoi ot osi na rasstoyanie $a$ . Pri otklonenii mayatnika ot vertikali na nebol'shoi ugol $\alpha$ on budet sovershat' svobodnye garmonicheskie kolebaniya pod deistviem sily tyazhesti, prilozhennoi k centru mass (ris. 1.2).

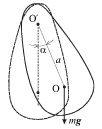Ris. 1.2.

Esli izvesten moment inercii tela $J$ otnositel'no osi vrasheniya, to uravnenie vrashatel'nogo dvizheniya zapishetsya v vide

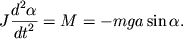$J{\displaystyle \frac{\displaystyle {\displaystyle d^{2}\alpha }}{\displaystyle {\displaystyle dt^{2}}}} = M = - mga\sin \alpha .$

(1.12)

Esli schitat', chto pri vrashenii, naprimer, protiv chasovoi strelki ugol $\alpha$ uvelichivaetsya, to moment sily tyazhesti $M$ vyzyvaet umen'shenie etogo ugla i, sledovatel'no, pri $\alpha \gt 0$ moment $M \lt 0.$ Eto i otrazhaet znak minus v pravoi chasti (1.12).

Dlya malyh uglov otkloneniya uravnenie (1.12) perehodit v uravnenie garmonicheskih kolebanii

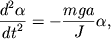${\displaystyle \frac{\displaystyle {\displaystyle d^{2}\alpha }}{\displaystyle {\displaystyle dt^{2}}}} = - {\displaystyle \frac{\displaystyle {\displaystyle mga}}{\displaystyle {\displaystyle J}}}\alpha,$

(1.13)

iz vida kotorogo srazu yasno, chto chastota $\omega _{0}$ i period $T$ kolebanii sootvetstvenno ravny

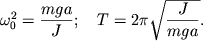$\omega _{0}^{2} = {\displaystyle \frac{\displaystyle {\displaystyle mga}}{\displaystyle {\displaystyle J}}}; \quad T = 2\pi \sqrt {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle J}}{\displaystyle {\displaystyle mga}}}} .$

(1.14)

Sravnivaya vyrazheniya dlya perioda kolebanii fizicheskogo (1.14) i matematicheskogo (1.11) mayatnikov, legko videt', chto oba perioda sovpadayut, esli

${\displaystyle \frac{\displaystyle {\displaystyle J}}{\displaystyle {\displaystyle ma}}} = \ell .$

(1.15)

Poetomu fizicheskii mayatnik harakterizuetsya privedennoi dlinoi (1.15), kotoraya ravna dline matematicheskogo mayatnika s takim zhe periodom kolebanii.

Period kolebanii fizicheskogo mayatnika (a, sledovatel'no, i ego privedennaya dlina $\ell$ ) nemonotonno zavisit ot rasstoyaniya $a$ . Eto legko zametit', esli v sootvetstvii s teoremoi Gyuigensa-Shteinera moment inercii $J$ vyrazit' cherez moment inercii $J_{0}$ otnositel'no parallel'noi gorizontal'noi osi, prohodyashei cherez centr mass: $J = J_{0} + ma^{2}.$ Togda period kolebanii (1.14) budet raven:

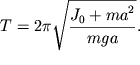$T = 2\pi \sqrt {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle J_{0} + ma^{2}}}{\displaystyle {\displaystyle mga}}}} .$

(1.16)

Izmenenie perioda kolebanii pri udalenii osi vrasheniya ot centra mass O v obe storony na rasstoyanie a pokazano na ris. 1.3.

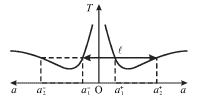Ris. 1.3.

Legko videt', chto odin i tot zhe period kolebanii mozhet realizovat'sya otnositel'no lyuboi iz chetyreh osei, raspolozhennyh poparno po raznye storony ot centra mass. Mozhno pokazat', chto summa rasstoyanii $a_{1}^{ + }$ i $a_{2}^{ + }$ ravna privedennoi dline fizicheskogo mayatnika: $\ell = a_{1}^{ + } + a_{2}^{ + } .$ V silu simmetrii grafika yasno, chto

$\ell = a_{2}^{ + } + a_{1}^{ - } .$

(1.17)

Eto obstoyatel'stvo pozvolyaet dlya lyuboi osi vrasheniya O⁺ opredelit' sopryazhennuyu os' O^-. Period kolebanii otnositel'no etih osei odinakov, a rasstoyanie mezhdu nimi ravno privedennoi dline fizicheskogo mayatnika.

Na ris. 1.4 izobrazheny polozheniya osei O⁺ i O^-, pri etom os' vrasheniya, udalennaya na rasstoyanie $a_{2}^{ - },$ pri takoi forme mayatnika nahoditsya vne ego.

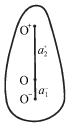Ris. 1.4.

Fizicheskii mayatnik primenyaetsya dlya izmereniya uskoreniya svobodnogo padeniya. S etoi cel'yu izmeryayut zavisimost' perioda kolebanii mayatnika ot polozheniya osi vrasheniya i po etoi eksperimental'noi zavisimosti nahodyat v sootvetstvii s formuloi (1.17) privedennuyu dlinu. Opredelennaya takim obrazom privedennaya dlina v sochetanii s izmerennym s horoshei tochnost'yu periodom kolebanii otnositel'no obeih osei pozvolyaet rasschitat' uskorenie svobodnogo padeniya. Vazhno otmetit', chto pri takom sposobe izmerenii ne trebuetsya opredelenie polozheniya centra mass, chto v ryade sluchaev povyshaet tochnost' izmerenii.

Nazad| Vpered

Publikacii s klyuchevymi slovami: kolebaniya - volny Publikacii so slovami: kolebaniya - volny
Sm. takzhe: Eho iz glubin krasnogo giganta

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce