Astronet > Kolebaniya i volny

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Kolebaniya i volny. Lekcii.

V.A.Aleshkevich, L.G.Dedenko, V.A.Karavaev (Fizicheskii fakul'tet MGU)
Izdatel'stvo Fizicheskogo fakul'teta MGU, 2001 g. Soderzhanie

Opredelim teper' skorost' $c_{p}$ dvizheniya etoi volny. Dlya etogo prosledim za dvizheniem grebnya volny, vershina kotorogo v nekotoryi moment vremeni nahoditsya v tochke $M.$ Pust' za vremya $\Delta t$ etot greben' smestitsya na rasstoyanie $\Delta x_{n} \gg a.$ Poskol'ku na vershine grebnya massy imeyut maksimal'noe polozhitel'noe smeshenie, to faza ih kolebanii postoyanna i ravna

$\omega _{p} t - k_{p} x_{n} = {\displaystyle \frac{\displaystyle {\displaystyle \pi }}{\displaystyle {\displaystyle 2}}}.$

(4.11)

Poetomu

$\omega _{p} \Delta t - k_{p} \Delta x_{n} = 0.$

(4.12)

Otsyuda skorost' $c_{p}$ poluchaetsya ravnoi

$c_{p} = {\displaystyle \frac{\displaystyle {\displaystyle \Delta x_{n} }}{\displaystyle {\displaystyle \Delta t}}} = {\displaystyle \frac{\displaystyle {\displaystyle \omega _{p} }}{\displaystyle {\displaystyle k_{p} }}} = \nu _{p} \cdot \lambda _{p}.$

(4.13)

Skorost' $c_{p}$ nazyvaetsya fazovoi skorost'yu garmonicheskoi volny s chastotoi $\omega _{p} = 2\pi \nu _{p}.$ Proanaliziruem zavisimost' etoi skorosti ot volnovogo chisla, pol'zuyas' dispersionnym sootnosheniem (4.1). Dlya etogo perepishem ego s uchetom (4.4) v vide:

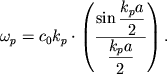$\omega _{p} = c_{0} k_{p} \cdot \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \sin {\displaystyle \frac{\displaystyle {\displaystyle k_{p} a}}{\displaystyle {\displaystyle 2}}}}}{\displaystyle {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle k_{p} a}}{\displaystyle {\displaystyle 2}}}}}}} \right).$

(4.14)

Grafik zavisimosti (4.14) nazyvaetsya dispersionnoi krivoi i izobrazhen na ris. 4.5a.

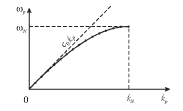Ris. 4.5a.

Na etoi krivoi tochkami otmecheny znacheniya chastot $\omega _{p}$ i volnovyh chisel $k_{p}.$ Punktirom izobrazhena pryamaya $\omega _{p} = c_{0} k_{p}.$ Ona poluchaetsya iz (4.14) predel'nym perehodom pri $a \to 0$ (nepreryvnaya sreda).

Iz formuly (4.14) ili iz ris. 4.5a mozhno sdelat' ryad principial'no vazhnyh vyvodov.

1) Iz nelineinoi zavisimosti $\omega _{p} = \omega (k_{p} ),$ opisyvaemoi formuloi (4.14), sleduet, chto fazovaya skorost' garmonicheskoi volny $c_{p} = \omega _{p} / k_{p}$ zavisit ot $k_{p}$ (ili ot $\omega _{p}$ ):

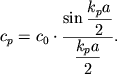$c_{p} = c_{0} \cdot {\displaystyle \frac{\displaystyle {\displaystyle \sin {\displaystyle \frac{\displaystyle {\displaystyle k_{p} a}}{\displaystyle {\displaystyle 2}}}}}{\displaystyle {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle k_{p} a}}{\displaystyle {\displaystyle 2}}}}}}.$

(4.15)

Zavisimost' (4.15) izobrazhena na ris. 4.5b.

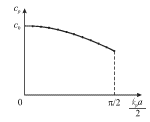Ris. 4.5b.

Eto yavlenie nosit nazvanie dispersii sredy po otnosheniyu k rasprostranyayusheisya v nei volne. Ekvivalentnym yavlyaetsya vyrazhenie "dispersiya volny v srede". Esli fazovaya skorost' volny ne zavisit ot $k_{p},$ kak, naprimer, v sluchae nepreryvnoi sredy, to govoryat, chto dispersiya otsutstvuet.

2) Dlya malen'kih volnovyh chisel ( $k_{p} a \ll 1,$ ili $\lambda _{p} \gg a$ ) dispersiya mala. Skorost' takih "dlinnyh voln" $c_{p} \approx c_{0},$ i sreda mozhet schitat'sya sploshnoi.

3) S uvelicheniem volnovogo chisla $k_{p}$ (a znachit i $\omega _{p}$ ) skorost' $c_{p},$ kak eto sleduet iz (4.15), ubyvaet. Takoe povedenie skorosti nazyvaetsya normal'noi dispersiei. Sleduet otmetit', chto v optike, pomimo etoi, realizuetsya i drugaya situaciya, kogda fazovaya skorost' sveta v nekotorom diapazone chastot mozhet vozrastat' s uvelicheniem chastoty. V etom sluchae dispersiya nazyvaetsya anomal'noi.

4) Dispersionnaya krivaya zakanchivaetsya, kogda volnovoe chislo i chastota dostigayut maksimal'nyh znachenii $k_{N}$ i $\omega _{N}.$ Oni poluchayutsya iz (4.14) i (4.1) pri $N \gg 1$ :

$k_{N} = {\displaystyle \frac{\displaystyle {\displaystyle \pi }}{\displaystyle {\displaystyle a}}}; \quad \omega _{N} = 2\Omega.$

Eto oznachaet, chto volny s chastotoi $\omega \gt \omega _{N}$ v takoi srede rasprostranyat'sya ne mogut. Deistvitel'no, pri chastote $\omega = \omega _{N}$ dlina volny $\lambda _{N} = 2\pi / k_{N} = 2a.$ Volny s men'shei dlinoi volny ne mogut sushestvovat', poskol'ku na dline rasprostranyayusheisya volny dolzhno nahodit'sya ne men'she dvuh koleblyushihsya gruzov.

Zametim, chto v nekotoryh sluchayah, naprimer, pri rasprostranenii elektromagnitnyh voln v tverdom tele i v plazme, krivaya dispersii mozhet nachinat'sya s nekotoroi tochki na osi chastot $\omega (0).$ V takih sredah mogut rasprostranyat'sya elektromagnitnye volny tol'ko s chastotami $\omega,$ lezhashimi vnutri intervala $\omega (0) \lt \omega \le \omega _{N}.$

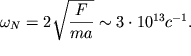V kachestve primera ukazhem, chto dlya kristallov velichina $F / a\sim 15 N/m$ ( $F$ - uprugaya sila, velichina kotoroi opredelyaetsya mezhatomnym vzaimodeistviem). Esli prinyat' massu iona ravnoi $m\sim 6 \cdot 10^{ - 26} kg,$ to $\omega _{N} = 2\sqrt {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle F}}{\displaystyle {\displaystyle ma}}}} \sim 3 \cdot 10^{13} c^{ - 1}.$ Eta chastota, kak i chastoty kolebanii molekul CO₂ i H₂O, lezhit v infrakrasnoi oblasti elektromagnitnogo spektra. Poetomu pri rasprostranenii IK izlucheniya v kristallah iony mogut sovershat' rezonansnye kolebaniya. V etom chastotnom opticheskom diapazone mozhet sushestvovat' sil'naya dispersiya sveta.

Otmetim, chto pri rasprostranenii voln v protyazhennyh sredah problemy "nastroiki" chastoty $\omega$ vneshnego vozdeistviya, porozhdayushego volnu, na chastotu $\omega _{p}$ odnoi iz mod sredy ne sushestvuet. Lyuboe vozdeistvie vneshnei sily, dazhe skol' ugodno blizkoi k garmonicheskoi, na samom dele vsegda budet kvazigarmonicheskim, harakterizuemym uzkim intervalom chastot $\Delta \omega \ll \omega.$ S drugoi storony, dlya protyazhennoi sredy k chastote $\omega$ budut blizki chastoty $\omega _{p}$ mod s bol'shimi nomerami $r (p \gg 1).$ Raznost' chastot dvuh sosednih mod $\Delta \omega _{p} = \omega _{p + 1} - \omega _{p},$ kak eto legko videt' iz risunka 4.5, budet nastol'ko maloi, chto $\Delta \omega _{p} \ll \Delta \omega.$ Sledovatel'no, dlya lyuboi chastoty $\omega$ vneshnego vozdeistviya, prikladyvaemogo k granice sredy, po nei pobezhit volna, kotoruyu v ryade sluchaev mozhno priblizhenno schitat' garmonicheskoi:

$s(x,t) = s_{0} \sin (\omega t - kx).$

(4.16)

Gruppa voln i ee skorost'.

Kak i vneshnee vozdeistvie, volna, voznikayushaya v srede, budet, strogo govorya, kvazigarmonicheskoi, t. k. $\Delta \omega _{p} \ll \Delta \omega.$ Poetomu vmesto (4.16) sleduet zapisat' uravnenie volny v bolee uslozhnennom vide:

$s(x,t) = s_{0} (x,t)\sin [\omega _{0} t - k_{0} x + \varphi _{0} (x,t)].$

(4.17)

Zdes' amplituda $s_{0} (x,t)$ i faza $\varphi _{0} (x,t)$ yavlyayutsya medlenno menyayushimisya funkciyami vremeni na nekotorom masshtabe vremeni $\tau$ (sravnite s formuloi (3.19)). Estestvenno, chto takaya volna predstavlyaet soboi gruppu garmonicheskih voln, chastoty kotoryh raspolagayutsya vblizi osnovnoi chastoty $\omega _{0}$ v predelah intervala $\Delta \omega \approx 2\pi / \tau.$ Kazhdaya iz voln gruppy v srede s dispersiei imeet sobstvennuyu fazovuyu skorost'. V srede s normal'noi dispersiei volny bol'shei chastoty budut dvigat'sya medlennee, chem volny men'shei chastoty. Voznikaet estestvennyi vopros: chto yavlyaetsya skorost'yu gruppy voln, i esli takaya skorost' sushestvuet, to kak ee vychislit'? Kakoi fizicheskii smysl imeet eta skorost' i v chem ee otlichie ot fazovoi skorosti ?

Chtoby otvetit' na eti voprosy, rassmotrim dlya prostoty gruppu iz dvuh voln s odinakovymi amplitudami $s_{0}$ i s blizkimi chastotami $\omega _{1}$ i $\omega _{2},$ begushih v polozhitel'nom napravlenii osi h. Budem schitat', chto $\Delta \omega = \omega _{2} - \omega _{1} \ll \omega _{0} = {\displaystyle \frac{\displaystyle {\displaystyle \omega _{1} + \omega _{2} }}{\displaystyle {\displaystyle 2}}}.$ S takoi situaciei my uzhe vstrechalis' pri analize bienii dvuh svyazannyh oscillyatorov. Zadadim dispersionnye svoistva sredy dispersionnym sootnosheniem $\omega = \omega (k).$ S ego pomosh'yu vychislim znacheniya $k_{1}$ i $k_{2}$ dvuh volnovyh chisel, sootvetstvuyushih chastotam $\omega _{1}$ i $\omega _{2}.$ Togda uravnenie gruppy voln primet vid:

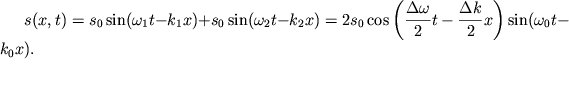$s(x,t) = s_{0} \sin (\omega _{1} t - k_{1} x) + s_{0} \sin (\omega _{2} t - k_{2} x) = 2s_{0} \cos \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \Delta \omega }}{\displaystyle {\displaystyle 2}}}t - {\displaystyle \frac{\displaystyle {\displaystyle \Delta k}}{\displaystyle {\displaystyle 2}}}x} \right)\sin (\omega _{0} t - k_{0} x).$

(4.18)

Zdes' $\Delta k = k_{2} - k_{1}, k_{0} = {\displaystyle \frac{\displaystyle {\displaystyle k_{1} + k_{2} }}{\displaystyle {\displaystyle 2}}}.$

Nazad| Vpered

Publikacii s klyuchevymi slovami: kolebaniya - volny Publikacii so slovami: kolebaniya - volny
Sm. takzhe: Eho iz glubin krasnogo giganta

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce