Astronet > Kolebaniya i volny

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Kolebaniya i volny. Lekcii.

V.A.Aleshkevich, L.G.Dedenko, V.A.Karavaev (Fizicheskii fakul'tet MGU)
Izdatel'stvo Fizicheskogo fakul'teta MGU, 2001 g. Soderzhanie

Na ris. 4.6 izobrazhena gruppa iz dvuh voln v nekotoryi fiksirovannyi moment vremeni $t_{0}.$ Vydelim dve tochki: M i R. Pervaya iz nih otvechaet fiksirovannomu znacheniyu fazy $\varphi _{M} = \omega _{0} t - k_{0} x_{M},$ pri kotoroi $\sin \varphi _{M} = 1.$ Ochevidno, chto skorost' etoi tochki, opredelyaemaya iz usloviya $d\varphi _{M} = \omega _{0} dt - k_{0} dx_{M} = 0,$ ravna

$c = {\displaystyle \frac{\displaystyle {\displaystyle dx_{M} }}{\displaystyle {\displaystyle dt}}} = {\displaystyle \frac{\displaystyle {\displaystyle \omega _{0} }}{\displaystyle {\displaystyle k_{0} }}}$

(4.19)

i sovpadaet s fazovoi skorost'yu volny s chastotoi $\omega _{0}.$

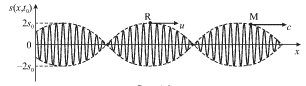Ris. 4.6.

Amplituda kvazigarmonicheskoi volny (4.18) opredelyaetsya kak

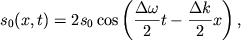$s_{0} (x,t) = 2s_{0} \cos \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \Delta \omega }}{\displaystyle {\displaystyle 2}}}t - {\displaystyle \frac{\displaystyle {\displaystyle \Delta k}}{\displaystyle {\displaystyle 2}}}x} \right),$

(4.20)

i ee raspredelenie na ris. 4.6 izobrazheno punktirom v vide medlenno menyayusheisya vdol' $h$ ogibayushei volny osnovnoi chastoty $\omega _{0}.$ Tochka R na vershine etoi ogibayushei budet dvigat'sya so skorost'yu, otlichayusheisya ot $s.$ Deistvitel'no, dlya koordinaty $x_{R}$ etoi tochki, kak eto sleduet iz (4.20), mozhem zapisat' uslovie

${\displaystyle \frac{\displaystyle {\displaystyle \Delta \omega }}{\displaystyle {\displaystyle 2}}}t - {\displaystyle \frac{\displaystyle {\displaystyle \Delta k}}{\displaystyle {\displaystyle 2}}}x_{R} = const.$

(4.21)

Za vremya dt ona smestitsya na rasstoyanie $dx_{R},$ kotoroe nahoditsya iz ravenstva:

${\displaystyle \frac{\displaystyle {\displaystyle \Delta \omega }}{\displaystyle {\displaystyle 2}}}dt - {\displaystyle \frac{\displaystyle {\displaystyle \Delta k}}{\displaystyle {\displaystyle 2}}}dx_{R} = 0.$

(4.22)

Sledovatel'no, skorost' dvizheniya vershiny ogibayushei budet ravna

$u = {\displaystyle \frac{\displaystyle {\displaystyle dx_{R} }}{\displaystyle {\displaystyle dt}}} = {\displaystyle \frac{\displaystyle {\displaystyle \Delta \omega }}{\displaystyle {\displaystyle \Delta k}}}.$

(4.23)

Eta skorost' harakterizuet dvizhenie gruppy voln i nazyvaetsya gruppovoi skorost'yu. Ee smysl stanet eshe bolee ponyatnym, esli v predelah intervala $\Delta \omega$ v gruppe budut nahodit'sya volny s blizko raspolozhennymi chastotami, kak, naprimer, izobrazheno na ris. 4.7a.

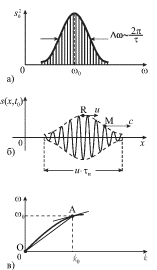Ris. 4.7.

Sama gruppa imeet vid odnogo impul'sa dlitel'nost'yu $\tau _{i},$ rasprostranyayushegosya vdol' osi h (ris. 4.7b). Impul's budet dvigat'sya s gruppovoi skorost'yu $u = d\omega / dk.$ Na dispersionnoi krivoi (ris. 4.7v) eta skorost' ravna uglovomu koefficientu kasatel'noi pryamoi v tochke A. "Sinusoida" vnutri impul'sa budet ego obgonyat' i dvigat'sya s fazovoi skorost'yu $c = \omega _{0} / k_{0}.$ Chislenno eta skorost' budet ravna uglovomu koefficientu otrezka OA. V srede bez dispersii dispersionnaya krivaya yavlyaetsya pryamoi liniei $\omega = ck.$ Poetomu

$c = {\displaystyle \frac{\displaystyle {\displaystyle \omega _{0} }}{\displaystyle {\displaystyle k_{_{0} } }}} = {\displaystyle \frac{\displaystyle {\displaystyle \Delta \omega }}{\displaystyle {\displaystyle \Delta k}}} = u,$

(4.24)

t.e. fazovaya i gruppovaya skorosti sovpadayut. V srede s normal'noi dispersiei, kak eto vidno iz ris. 4.7v, $u \lt c.$ V srede s anomal'noi dispersiei krivaya $\omega = \omega (k)$ dolzhna zagibat'sya vverh i, formal'no, $u \gt c.$ Odnako obychno eta zavisimost' nastol'ko nelineina, chto ponyatie gruppovoi skorosti teryaet smysl.

Deistvitel'no, kogda impul's, izobrazhennyi na ris. 4.7b, proidet ochen' bol'shoe rasstoyanie v dispergiruyushei srede, to forma ego iskazitsya, i on rastyanetsya v prostranstve. V srede s sil'noi anomal'noi dispersiei eto iskazhenie proishodit uzhe na malyh rasstoyaniyah, poetomu govorit' o rasprostranenii impul'sa kak celogo s gruppovoi skorost'yu $u$ nekorrektno.

Dispersionnoe ushirenie impul'sov negativno skazyvaetsya, naprimer, na skorosti peredachi informacii (kolichestvo bit v edinicu vremeni) posredstvom korotkih svetovyh impul'sov, begushih po volokonno-opticheskim liniyam svyazi, dlina kotoryh dostigaet neskol'kih tysyach kilometrov. Dva sleduyushih drug za drugom impul'sa mogut rasshirit'sya nastol'ko, chto sol'yutsya v odin (stanut nerazlichimymi). Estestvenno, chto priemnik, ustanovlennyi v konce linii, "vosprimet" dva impul'sa kak odin, i chast' peredavaemoi informacii budet uteryana.

Volnovoe uravnenie.

Uravnenie begushei garmonicheskoi volny v odnorodnom shnure, gde dispersiya otsutstvuet $(\omega = c_{0} k),$ po analogii s (4.16) imeet vid:
$s(x,t) = s_{0} \sin (\omega t \mp kx) = s_{0} \sin {\displaystyle \left[ {\displaystyle \omega \left( {\displaystyle t \mp {\displaystyle \frac{\displaystyle {\displaystyle x}}{\displaystyle {\displaystyle c_{0} }}}} \right)} \right]}.$ (4.25)

Znak "-" sootvetstvuet volne, begushei v polozhitel'nom napravlenii po osi Ox, a znak "+" - v otricatel'nom.

V bolee obshem sluchae rasprostraneniya proizvol'nogo impul'sa (gruppy voln), dvigayushegosya s toi zhe skorost'yu $c_{0},$ uravnenie volny mozhno zapisat' v vide:

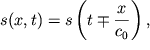$s(x,t) = s\left( {\displaystyle t \mp {\displaystyle \frac{\displaystyle {\displaystyle x}}{\displaystyle {\displaystyle c_{0} }}}} \right),$

(4.26)

gde $s(\theta )$ - proizvol'naya funkciya svoego argumenta $\theta = t \mp x / c_{0}.$

Pokazhem, chto zakon dvizheniya shnura (4.26) i, konechno, ego chastnyi sluchai (4.25) yavlyayutsya resheniyami nekotorogo uravneniya dvizheniya, kotoroe nazyvaetsya volnovym uravneniem. Eto volnovoe uravnenie mozhno poluchit' predel'nym perehodom iz uravneniya (3.47).

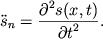Na ris. 4.8 pokazan fragment koleblyushegosya shnura. Na etom fragmente izobrazheny tri otrezka shnura dlinoi $\Delta x$ i massoi $dm$ kazhdyi. Smesheniya etih otrezkov v nekotoryi proizvol'nyi moment vremeni ravny $s_{n - 1} = s(x - \Delta x,t),\; s_{n} = s(x,t),\; s_{n + 1} = s(x + \Delta x,t).$ Uskorenie central'nogo otrezka $\ddot {\displaystyle s}_{n} = {\displaystyle \frac{\displaystyle {\displaystyle \partial ^{2}s(x,t)}}{\displaystyle {\displaystyle \partial t^{2}}}}.$ Ono zapisano v vide vtoroi chastnoi proizvodnoi funkcii $s(x,t)$ po vremeni. Uchtem dalee, chto

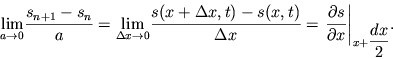${\displaystyle \mathop {\displaystyle \lim }\limits_{a \to 0} }{\displaystyle \frac{\displaystyle {\displaystyle s_{n + 1} - s_{n} }}{\displaystyle {\displaystyle a}}} = {\displaystyle \mathop {\displaystyle \lim }\limits_{\Delta x \to 0} }{\displaystyle \frac{\displaystyle {\displaystyle s(x + \Delta x,t) - s(x,t)}}{\displaystyle {\displaystyle \Delta x}}} = {\displaystyle \left. {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial x}}}} \right|}_{x + {\displaystyle \frac{\displaystyle {\displaystyle dx}}{\displaystyle {\displaystyle 2}}}}.$

(4.27a)

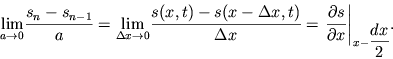${\displaystyle \mathop {\displaystyle \lim }\limits_{a \to 0} }{\displaystyle \frac{\displaystyle {\displaystyle s_{n} - s_{n - 1} }}{\displaystyle {\displaystyle a}}} = {\displaystyle \mathop {\displaystyle \lim }\limits_{\Delta x \to 0} }{\displaystyle \frac{\displaystyle {\displaystyle s(x,t) - s(x - \Delta x,t)}}{\displaystyle {\displaystyle \Delta x}}} = {\displaystyle \left. {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial x}}}} \right|}_{x - {\displaystyle \frac{\displaystyle {\displaystyle dx}}{\displaystyle {\displaystyle 2}}}}.$

(4.27b)

Ris. 4.8.

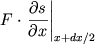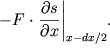Obratim vnimanie, chto sila $F \cdot {\displaystyle \left. {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial x}}}} \right|}_{x + dx / 2}$ yavlyaetsya proekciei na napravlenie smesheniya s sily $F,$ prilozhennoi k central'nomu elementu sprava (v tochke $x + dx / 2$ ). Analogichno, sleva (v tochke $x - dx / 2$ ) proekciya etoi sily ravna $- F \cdot {\displaystyle \left. {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial x}}}} \right|}_{x - dx / 2}.$ Ravnodeistvuyushaya etih sil, ochevidno, opredelyaetsya prirasheniem pervoi proizvodnoi na dline beskonechno malogo elementa $dx$ :

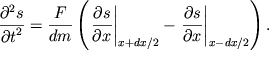${\displaystyle \frac{\displaystyle {\displaystyle \partial ^{2}s}}{\displaystyle {\displaystyle \partial t^{2}}}} = {\displaystyle \frac{\displaystyle {\displaystyle F}}{\displaystyle {\displaystyle dm}}}\left( {\displaystyle {\displaystyle \left. {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial x}}}} \right|}_{x + dx / 2} - {\displaystyle \left. {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial x}}}} \right|}_{x - dx / 2} } \right).$

(4.28)

Esli teper' uchest', chto $dm = \rho _{1} dx$ ( $\rho _{1}$ - plotnost' edinicy dliny, ili lineinaya plotnost' shnura), to (4.28) primet vid volnovogo uravneniya:

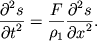(4.29)

Eto volnovoe uravnenie yavlyaetsya matematicheskim vyrazheniem vtorogo zakona N'yutona, v kotorom uskorenie edinicy dliny shnura i deistvuyushaya na nego sila zapisany v vide vtoryh chastnyh proizvodnyh smesheniya $s$ po vremeni i koordinate sootvetstvenno. S matematicheskoi tochki zreniya ono yavlyaetsya lineinym differencial'nym uravneniem s chastnymi proizvodnymi vtorogo poryadka. Ego reshenie horosho izvestno: im mozhet byt' lyubaya funkciya $s\left( {\displaystyle \theta } \right),$ argument kotoroi "skonstruirovan" v vide (4.26), a skorost' 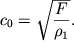$c_{0} = \sqrt {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle F}}{\displaystyle {\displaystyle \rho _{1} }}}}.$ Ubedimsya v spravedlivosti etogo utverzhdeniya. Dlya etogo vychislim vtorye proizvodnye v sootvetstvii s pravilami differencirovaniya funkcii so slozhnym argumentom $\theta = t \mp {\displaystyle \frac{\displaystyle {\displaystyle x}}{\displaystyle {\displaystyle c_{0} }}}$ :

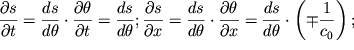${\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial t}}} = {\displaystyle \frac{\displaystyle {\displaystyle ds}}{\displaystyle {\displaystyle d\theta }}} \cdot {\displaystyle \frac{\displaystyle {\displaystyle \partial \theta }}{\displaystyle {\displaystyle \partial t}}} = {\displaystyle \frac{\displaystyle {\displaystyle ds}}{\displaystyle {\displaystyle d\theta }}}; {\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial x}}} = {\displaystyle \frac{\displaystyle {\displaystyle ds}}{\displaystyle {\displaystyle d\theta }}} \cdot {\displaystyle \frac{\displaystyle {\displaystyle \partial \theta }}{\displaystyle {\displaystyle \partial x}}} = {\displaystyle \frac{\displaystyle {\displaystyle ds}}{\displaystyle {\displaystyle d\theta }}} \cdot \left( {\displaystyle \mp {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle c_{0} }}}} \right);$

(4.30)

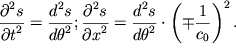${\displaystyle \frac{\displaystyle {\displaystyle \partial ^{2}s}}{\displaystyle {\displaystyle \partial t^{2}}}} = {\displaystyle \frac{\displaystyle {\displaystyle d^{2}s}}{\displaystyle {\displaystyle d\theta ^{2}}}}; {\displaystyle \frac{\displaystyle {\displaystyle \partial ^{2}s}}{\displaystyle {\displaystyle \partial x^{2}}}} = {\displaystyle \frac{\displaystyle {\displaystyle d^{2}s}}{\displaystyle {\displaystyle d\theta ^{2}}}} \cdot \left( {\displaystyle \mp {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle c_{0} }}}} \right)^{2}.$

(4.31)

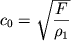Podstavlyaya vtorye proizvodnye iz (4.31) v (4.29), prihodim k vyvodu, chto pri $c_{0} = \sqrt {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle F}}{\displaystyle {\displaystyle \rho _{1} }}}}$ uravnenie (4.29) tozhdestvenno udovletvoryaetsya, t.e. funkciya $s\left( {\displaystyle \theta } \right)$ deistvitel'no yavlyaetsya ego resheniem.

Volnovoe uravnenie yavlyaetsya odnim iz fundamental'nyh uravnenii. V raznyh oblastyah fiziki eto uravnenie poluchaetsya kak rezul'tat primeneniya sootvetstvuyushih zakonov, opisyvayushih povedenie sistem razlichnoi prirody (mehanicheskih, elektromagnitnyh i dr.). V obshem sluchae ono opisyvaet rasprostranenie voln v trehmernom prostranstve i imeet bolee slozhnyi vid:

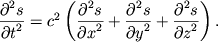${\displaystyle \frac{\displaystyle {\displaystyle \partial ^{2}s}}{\displaystyle {\displaystyle \partial t^{2}}}} = c^{2}\left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \partial ^{2}s}}{\displaystyle {\displaystyle \partial x^{2}}}} + {\displaystyle \frac{\displaystyle {\displaystyle \partial ^{2}s}}{\displaystyle {\displaystyle \partial y^{2}}}} + {\displaystyle \frac{\displaystyle {\displaystyle \partial ^{2}s}}{\displaystyle {\displaystyle \partial z^{2}}}}} \right).$

(4.32)

Pod $s$ mozhet podrazumevat'sya lyubaya koleblyushayasya velichina: smeshenie, skorost', plotnost', davlenie, elektricheskii tok, elektricheskoe napryazhenie, napryazhennost' elektricheskogo i indukciya magnitnogo polei i dr.

Vazhno podcherknut', chto esli nam udaetsya poluchit' volnovoe uravnenie (vyvesti ego) dlya kakogo-libo processa, to stoyashii pered vtorymi prostranstvennymi proizvodnymi mnozhitel' srazu opredelyaet kvadrat skorosti rasprostraneniya volny v srede bez dispersii. Etim priemom chasto pol'zuyutsya dlya vychisleniya skorosti rasprostraneniya voln razlichnoi prirody. Nizhe my tozhe tak postupim, kogda budem rassmatrivat' volny v tverdyh telah, zhidkostyah i gazah.

Nazad| Vpered

Publikacii s klyuchevymi slovami: kolebaniya - volny Publikacii so slovami: kolebaniya - volny
Sm. takzhe: Eho iz glubin krasnogo giganta

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce