Astronet > Kolebaniya i volny

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Kolebaniya i volny. Lekcii.

V.A.Aleshkevich, L.G.Dedenko, V.A.Karavaev (Fizicheskii fakul'tet MGU)
Izdatel'stvo Fizicheskogo fakul'teta MGU, 2001 g. Soderzhanie

Otrazhenie volny na konce shnura.

My uzhe upominali v nachale etoi lekcii, chto volna, dostignuv konca shnura, otrazitsya. Harakter etogo otrazheniya zavisit ot uslovii zakrepleniya konca shnura (granichnyh uslovii).

Rassmotrim vnachale bolee podrobno process otrazheniya impul'sa ot zakreplennogo konca shnura.

Na ris. 4.9 pokazany posledovatel'nye stadii otrazheniya impul'sa treugol'noi formy, gde punktirom izobrazheny "padayushii" i "otrazhennyi" impul'sy. Esli dlitel'nost' impul'sa ravna $\tau _{i},$ to ego protyazhennost' vdol' struny ravna $c_{0} \tau _{i}.$ Pust' v moment vremeni $t = 0$ on dobezhit do konca struny. V posleduyushie momenty vremeni shnur budet vozdeistvovat' na kronshtein, k kotoromu prikreplen ego konec, s peremennoi siloi, perpendikulyarnoi napravleniyu dvizheniya impul'sa. Eta sila v moment vremeni $t \gt 0$ nachinaet tyanut' kronshtein vverh. V techenii vremeni $0 \lt t \lt \tau _{i} / 2$ ona ostaetsya postoyannoi, i v moment vremeni $t = \tau _{i} / 2$ stanovitsya ravnoi nulyu. Po tret'emu zakonu N'yutona s takoi zhe siloi kronshtein deistvuet vniz na konec shnura. V moment vremeni $t = \tau _{i} / 2$ shnur stanovitsya pryamym. Odnako chast' shnura dlinoi $\frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}c\tau _{i$ prodolzhaet dvigat'sya vniz po inercii. Pri $t \gt {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}\tau _{i}$ shnur tyanet kronshtein vniz, i eto deistvie prekrashaetsya pri $t = \tau _{i}.$ Estestvenno, chto kronshtein vozdeistvuet na konec shnura s siloi, napravlennoi vverh, tormozya dvizhenie ego elementov vniz. Okonchatel'no poperechnoe deistvie shnura na kronshtein prekratitsya pri $t \gt \tau _{i},$ kogda sformiruetsya otrazhennyi impul's, imeyushii protivopolozhnuyu (po otnosheniyu k padayushemu) polyarnost'.

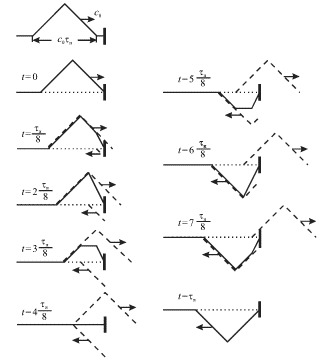Ris. 4.9.

Esli po shnuru bezhit garmonicheskaya volna, to po dostizhenii zakreplennogo konca shnura voznikaet obrashennaya otrazhennaya volna. Chtoby uchest' izmenenie ee polyarnosti, v argument uravneniya otrazhennoi volny dobavlyayut fazovyi sdvig $\varphi _{otr} = \pi.$ Poetomu govoryat, chto v etom sluchae pri otrazhenii faza volny skachkom menyaetsya na $\pi,$ ili "teryaetsya polvolny". V obshem sluchae pri proizvol'nyh granichnyh usloviyah sdvig fazy $\varphi _{otr}$ mozhet menyat'sya v intervale $0 \le \varphi _{otr} \le \pi.$ Poyasnim skazannoe prosteishim raschetom.

Pust' po shnuru bezhit garmonicheskaya volna. Dostignuv konca shnura pri $x = \ell ,$ ona budet otrazhat'sya (ris. 4.10). Smeshenie lyubogo uchastka struny, imeyushego koordinatu $x \le \ell,$ opredelyaetsya kak superpoziciya begushei i otrazhennoi voln:

$s(x,t) = s_{0} \sin (\omega t - kx) + s_{0} \sin [\omega t - k(2\ell - x) + \varphi _{otr} ].$

(4.33)

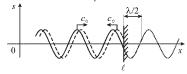Ris. 4.10.

V (4.33) uchteno, chto otrazhennaya volna, vo-pervyh, prohodit rasstoyanie "tuda i obratno", ravnoe $\ell + \left( {\displaystyle \ell - x} \right) = 2\ell - x,$ i, vo-vtoryh, priobretaet sdvig fazy $\varphi _{otr}$ pri ee otrazhenii. Provedem summirovanie v (4.33) i poluchim:

$s(x,t) = 2s_{0} \cos {\displaystyle \left[ {\displaystyle k(\ell - x) + {\displaystyle \frac{\displaystyle {\displaystyle \varphi _{otr} }}{\displaystyle {\displaystyle 2}}}} \right]}\sin {\displaystyle \left[ {\displaystyle \omega t - k\ell + {\displaystyle \frac{\displaystyle {\displaystyle \varphi _{otr} }}{\displaystyle {\displaystyle 2}}}} \right]}.$

(4.34)

Polagaem, chto amplituda volny $s_{0}$ ostaetsya postoyannoi pri rasprostranenii i ne menyaetsya pri otrazhenii.

Eto vyrazhenie yavlyaetsya uravneniem stoyachei volny. Osnovnye ee harakteristiki mogut byt' svedeny k sleduyushim:

1. V stoyachei volne vse uchastki shnura koleblyutsya s odinakovoi chastotoi $\omega$ i v faze, odnako amplituda etih kolebanii menyaetsya vdol' shnura, t.e. stoyachaya volna yavlyaetsya modoi kolebanii.

2. Amplituda kolebanii v stoyachei volne poluchaetsya iz (4.34) ravnoi:

$A(x) = 2s_{0} \cos {\displaystyle \left[ {\displaystyle k(\ell - x) + {\displaystyle \frac{\displaystyle {\displaystyle \varphi _{otr} }}{\displaystyle {\displaystyle 2}}}} \right]}.$

(4.35)

Iz etogo vyrazheniya vidno, chto nekotorye uchastki shnura koleblyutsya s amplitudoi, ravnoi $2s_{0}.$ Eto tak nazyvaemye "puchnosti" stoyachei volny. S drugoi storony, sushestvuyut uchastki, kotorye ostayutsya nepodvizhnymi, t. k. dlya nih amplituda $A = 0.$ Eto tak nazyvaemye "uzly" stoyachei volny.

Na ris 4.11 izobrazheny smesheniya fragmenta struny dlya treh posledovatel'nyh momentov vremeni $t_{1}, t_{2}$ i $t_{3}.$ Netrudno pokazat', chto rasstoyaniya mezhdu dvumya sosednimi uzlami, ukazannymi tochkami, ravno rasstoyaniyu mezhdu dvumya sosednimi puchnostyami, otmechennymi krestikami, i sostavlyaet velichinu $\Delta x = {\displaystyle \frac{\displaystyle {\displaystyle \pi }}{\displaystyle {\displaystyle k}}} = {\displaystyle \frac{\displaystyle {\displaystyle \lambda }}{\displaystyle {\displaystyle 2}}}.$

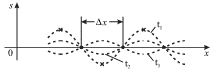Ris. 4.11.

3. Vse chasti shnura, lezhashie mezhdu dvumya sosednimi uzlami, sovershayut kolebaniya v faze. Pri perehode cherez uzel faza kolebanii skachkom izmenyaetsya na $\pi,$ chto sootvetstvuet izmeneniyu znaka $A(x).$

4. Na konce shnura $(x - \ell )$ amplituda

$A(\ell ) = 2s_{0} \cos {\displaystyle \frac{\displaystyle {\displaystyle \varphi _{otr} }}{\displaystyle {\displaystyle 2}}}.$

(4.36)

Dlya zakreplennogo konca shnura $A(\ell ) = 0$ i $\varphi _{otr} = \pi.$ Na ris. 4.10 pokazan uchastok v polvolny, kotoryi "teryaetsya" pri takom otrazhenii. Raspolozhennaya pravee etogo uchastka chast' volny, izobrazhennaya punktirom v oblasti $x \gt \ell,$ posle povorota napravleniya rasprostraneniya kak raz i budet yavlyat'sya volnoi, otrazhennoi v zakreplennoi tochke $x = \ell .$

Obratimsya teper' k otrazheniyu volny ot svobodnogo konca shnura. Tehnicheski eto mozhno realizovat', esli konec shnura privyazat' k tonkoi i legkoi niti, kotoraya sluzhit lish' dlya sozdaniya natyazheniya shnura s siloi $F.$

Process otrazheniya treugol'nogo impul'sa ot svobodnogo konca shnura pokazan na ris. 4.12. Obrashayut na sebya vnimanie dva obstoyatel'stva:

Otrazhennyi impul's sohranyaet tu zhe polyarnost', chto i padayushii. Eto svyazano s tem, chto pri dvizhenii svobodnyi konec budet tyanut' vverh prilegayushie k nemu sleva uchastki shnura, i, v rezul'tate, budet vozbuzhden otrazhennyi impul's, v kotorom elementy shnura takzhe smesheny vverh. V sluchae garmonicheskoi volny otrazhennaya volna nahoditsya v faze s padayushei. 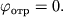Obrazuyushayasya stoyachaya volna budet opisyvat'sya uravneniem (4.34), v kotorom $\varphi _{otr} = 0.$
Konec shnura sovershaet "vzmah", velichina kotorogo vdvoe prevyshaet amplitudu impul'sa v ego seredine. Dlya garmonicheskoi volny na konce shnura 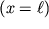$(x = \ell )$ obrazuetsya puchnost' stoyachei volny. Eto sleduet iz formuly (4.36), v kotoroi sleduet polozhit'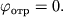 $\varphi _{otr} = 0.$

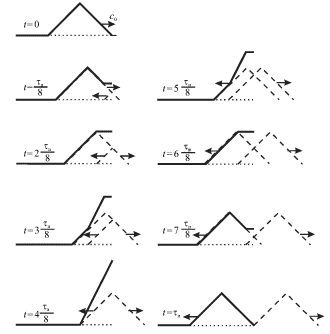Ris. 4.12.

Vozbuzhdenie stoyachih voln v shnure. Mody kolebanii.

Pust' kronshtein, k kotoromu privyazan levyi konec shnura, sovershaet garmonicheskie kolebaniya $s(t) = \xi _{0} \sin \omega t,$ gde $\xi _{0}$ - ochen' malaya amplituda. Poetomu levyi konec shnura mozhno schitat' zakreplennym. Po shnuru pobezhit garmonicheskaya volna (ris. 4.13), kotoraya posle otrazheniya ot pravogo zakreplennogo konca priobretet sdvig fazy, ravnyi $\pi.$ Dobezhav do levogo konca, ona eshe raz otrazitsya, a sdvig fazy stanet ravnym $2\pi.$

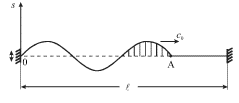Ris. 4.13.

Dvukratno otrazhennaya volna nalozhitsya na postoyanno begushuyu vpravo garmonicheskuyu volnu. Esli sdvig fazy kolebanii u etih voln budet kratnym velichine $2\pi,$ to rezul'tatom nalozheniya budet volna, amplituda kotoroi prevyshaet amplitudu $\xi _{0}$ ishodnoi begushei volny. Takim obrazom, begushaya volna usilitsya. Esli by ne bylo poter' energii, to narastanie amplitudy pri mnogokratnom otrazhenii bylo by neogranichennym. Odnako poteri, kak my ne raz videli, takzhe uvelichatsya s rostom amplitudy. Poetomu kolebaniya ustanovyatsya: v sistemu budet zakachano nekotoroe kolichestvo energii, a dal'neishii pritok ee budet raven dissipacii.

Opredelim chastotu vneshnego vozdeistviya $\omega,$ s kotoroi sleduet dvigat' levyi kronshtein, chtoby obespechit' maksimal'noe usilenie volny. Poskol'ku begushaya garmonicheskaya volna mozhet rassmatrivat'sya kak nabor sleduyushih drug za drugom so skorost'yu $c_{0}$ impul'sov raznoi polyarnosti, to my prosledim za usileniem lyubogo iz nih (naprimer, zashtrihovannogo na ris. 4.13). Vremya dvizheniya impul'sa (dlya opredelennosti tochki A v ego nachale) po shnuru tuda i obratno ravno $\Delta t = 2\ell / c_{0}.$ Uchtem dalee, chto posle dvuh otrazhenii etot impul's dva raza obratitsya. Dlya ego usileniya neobhodimo, chtoby v moment $t = \Delta t$ levyi konec shnura prohodil polozhenie ravnovesiya i dvigalsya pri etom vverh:

$\begin{array}{l} s(\Delta t) = \xi {\displaystyle }_{0}\sin (\omega \Delta t) = 0, \\ \dot {\displaystyle s}(\Delta t) = \xi _{0} \omega \cos (\omega \Delta t) = + \xi _{0} \omega. \\ \end{array}$

(4.37)

Poetomu chastota $\omega$ dolzhna udovletvoryat' usloviyu

$\omega _{p} \Delta t = 2\pi p,$

(4.38)

gde $p = I, II, III, \ldots$

Otsyuda

$\omega _{p} = {\displaystyle \frac{\displaystyle {\displaystyle \pi c_{0} }}{\displaystyle {\displaystyle \ell }}}p.$

(4.39)

Konfiguraciyu koleblyusheisya struny na chastotah (4.39) mozhno legko narisovat', kogda amplitudy begushei i otrazhennoi voln ne menyayutsya vdol' shnura i ravny mezhdu soboi. Ochevidno, chto eto budut stoyachie volny, rassmotrennye nami vyshe i sootvetstvuyushie odinakovym granichnym usloviyam: na oboih koncah shnura dolzhny byt' uzly smesheniya.

Nazad| Vpered

Publikacii s klyuchevymi slovami: kolebaniya - volny Publikacii so slovami: kolebaniya - volny
Sm. takzhe: Eho iz glubin krasnogo giganta

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce