Astronet > Kolebaniya i volny

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Kolebaniya i volny. Lekcii.

V.A.Aleshkevich, L.G.Dedenko, V.A.Karavaev (Fizicheskii fakul'tet MGU)
Izdatel'stvo Fizicheskogo fakul'teta MGU, 2001 g. Soderzhanie

Dlya primera na ris. 4.14 izobrazheny tri vozmozhnye konfiguracii shnura v moment vremeni, kogda smesheniya elementov shnura maksimal'ny. Kolebaniya, sootvetstvuyushie etim konfiguraciyam, yavlyayutsya normal'nymi kolebaniyami (modami), a chastoty $\omega _{I}, \omega _{II}, \omega _{III}$ - normal'nymi chastotami. Esli deistvie vneshnei sily prekratitsya, to eti kolebaniya budut prodolzhat'sya kak sobstvennye, poka ne zatuhnut.

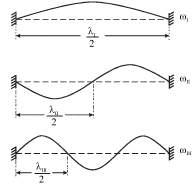Ris. 4.14.

Uslovie (4.39) mozhno perepisat' v bolee naglyadnom vide, esli pereiti ot chastoty $\omega _{p}$ k dline volny $\lambda _{p} = 2\pi c_{0} / \omega _{p}$ :

$\ell = p{\displaystyle \frac{\displaystyle {\displaystyle \lambda _{p} }}{\displaystyle {\displaystyle 2}}}.$

(4.40)

Eto uslovie oznachaet, chto pri normal'nyh kolebaniyah na dline shnura dolzhno ukladyvat'sya celoe chislo poluvoln. Legko teper' videt', chto kazhdaya iz mod mozhet byt' vozbuzhdena, esli prikladyvat' silu nuzhnoi chastoty k lyubomu uchastku shnura, za isklyucheniem teh, kotorye sovpadayut s uzlami dannoi mody.

Vidoizmenim granichnye usloviya i sdelaem oba konca shnura svobodnymi (privyazhem ih k natyanutym legkim nityam). Podschitaem chastoty vynuzhdayushei sily, na kotoryh vozbuzhdayutsya stoyachie volny (mody). Uchtem, chto posle dvuh otrazhenii impul's ne menyaet svoyu polyarnost', poetomu uslovie (4.40) ostanetsya prezhnim.

Na ris. 4.15 pokazany konfiguracii mod dlya shnura so svobodnymi koncami. Vidno, chto pri normal'nyh kolebaniyah na dline shnura takzhe dolzhno ukladyvat'sya celoe chislo poluvoln, no takim obrazom, chtoby na koncah shnura byli puchnosti.

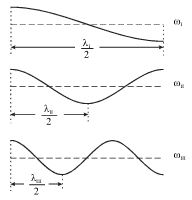Ris. 4.15.

Zakrepim teper' tol'ko levyi konec shnura i budem dvigat' kronshtein s maloi amplitudoi $\xi _{0}.$ Uslovie optimal'nogo vozbuzhdeniya stoyachih voln (mod) poluchaetsya iz teh soobrazhenii, chto impul's obrashaetsya tol'ko pri otrazhenii ot levogo konca shnura. Dlya usileniya impul'sa neobhodimo, chtoby levyi konec v moment vremeni $t = \Delta t$ dvigalsya vniz, prohodya polozhenie ravnovesiya:

$\begin{array}{l} s(\Delta t) = \xi {\displaystyle }_{0}\sin (\omega \Delta t) = 0, \\ \dot {\displaystyle s}(\Delta t) = \xi _{0} \omega \cos (\omega \Delta t) = - \xi _{0} \omega. \\ \end{array}$

(4.41)

Poetomu chastota \omega dolzhna udovletvoryat' usloviyu

$\omega _{p} \Delta t = (2p - 1)\pi,$

(4.42)

gde $p = I, II, III, \ldots$

Otsyuda

$\omega _{p} = {\displaystyle \frac{\displaystyle {\displaystyle \pi c_{0} }}{\displaystyle {\displaystyle 2\ell }}}(2p - 1).$

(4.43)

Poslednee uslovie stanovitsya bolee naglyadnym, esli pereiti k dline volny $\lambda _{p}$ :

$\ell = (2p - 1){\displaystyle \frac{\displaystyle {\displaystyle \lambda _{p} }}{\displaystyle {\displaystyle 4}}},$

(4.44)

gde $p = I, II, III, \ldots$ .

Sootvetstvuyushie tri nizshie mody izobrazheny na ris. 4.16. Ochevidno, chto eto budut stoyachie volny, otvechayushie raznym granichnym usloviyam: na levom konce dolzhen byt' uzel, a na pravom - puchnost'. Na dline shnura pri etom ukladyvaetsya nechetnoe chislo chetvertei dlin voln.

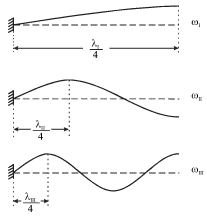Ris. 4.16.

Zamechanie. Pri vozbuzhdenii mody my zadavali zakon dvizheniya zakreplennogo konca shnura v vide $s(t) = \xi _{0} \sin \omega t,$ chto mozhet vyzvat' u chitatelya nekotoroe nedoumenie - kak mozhet dvigat'sya zakreplennyi konec? Odnako amplituda kolebanii $\xi _{0}$ obychno znachitel'no men'she amplitudy kolebanii v puchnostyah, poetomu neznachitel'no vibriruyushii konec shnura mozhet rassmatrivat'sya, kak nepodvizhnyi.

Volny v uprugih telah.

Kak my videli, sily vzaimodeistviya mezhdu sosednimi koleblyushimisya elementami shnura obespechivayut rasprostranenie v nem voln. V uprugih telah takie sily svodyatsya k kasatel'nym i normal'nym napryazheniyam, voznikayushim pri deformaciyah sdviga i rastyazheniya (szhatiya). Etim deformaciyam sootvetstvuyut 2 tipa voln: poperechnye i prodol'nye. Rassmotrim eti volny po otdel'nosti.

Poperechnye volny.

Esli po sterzhnyu, izgotovlennomu iz uprugogo materiala, udarit' molotkom v ego srednei chasti (ris. 4.17), to k ego koncam pobegut impul'sy, kak eto imelo mesto v shnure s gruzami, izobrazhennom na ris. 4.1. Odnako poperechnye smesheniya chastic sterzhnya budut nezametny dlya glaza, poetomu dlya registracii begushih po sterzhnyu vozmushenii trebuyutsya special'nye metody.

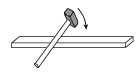Ris. 4.17.

Poskol'ku dispersiya voln mehanicheskoi prirody v sploshnoi srede otsutstvuet, to skorost' ih rasprostraneniya mozhno rasschitat' s pomosh'yu volnovogo uravneniya.

Na ris. 4.18 pokazan fragment koleblyushegosya sterzhnya. Na srednii element dlinoi $dx$ deistvuyut kasatel'nye napryazheniya (sleva $\sigma _{\tau } (x)$ i sprava $\sigma _{\tau } (x + dx)$ ), velichiny kotoryh proporcional'ny deformaciyam sdviga sosednih elementov:

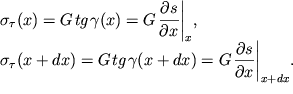$\begin{array}{l} \sigma _{\tau } (x) = G{\displaystyle \kern 1pt} tg{\displaystyle \kern 1pt} \gamma (x) = G{\displaystyle \left. {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial x}}}} \right|}_{x}, \\ \sigma _{\tau } (x + dx) = G{\displaystyle \kern 1pt} tg{\displaystyle \kern 1pt} \gamma (x + dx) = G{\displaystyle \left. {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial x}}}} \right|}_{x + dx}. \\ \end{array}$

(4.45)

Zdes' $G$ - modul' sdviga, $\gamma$ - ugol sdviga.

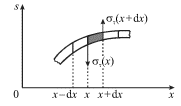Ris. 4.18.

Esli ploshad' poperechnogo secheniya sterzhnya ravna $S,$ to massa elementa $dm = S\rho dx$ ( $\rho$ - plotnost' materiala). Sledovatel'no, uravnenie ego dvizheniya mozhet byt' zapisano v vide:

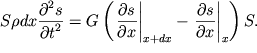$S\rho dx{\displaystyle \frac{\displaystyle {\displaystyle \partial ^{2}s}}{\displaystyle {\displaystyle \partial t^{2}}}} = G\left( {\displaystyle {\displaystyle \left. {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial x}}}} \right|}_{x + dx} - {\displaystyle \left. {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial x}}}} \right|}_{x} } \right)S.$

(4.46)

Podeliv obe chasti (4.46) na $S$ i $dx,$ poluchaem volnovoe uravnenie

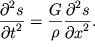${\displaystyle \frac{\displaystyle {\displaystyle \partial ^{2}s}}{\displaystyle {\displaystyle \partial t^{2}}}} = {\displaystyle \frac{\displaystyle {\displaystyle G}}{\displaystyle {\displaystyle \rho }}}{\displaystyle \frac{\displaystyle {\displaystyle \partial ^{2}s}}{\displaystyle {\displaystyle \partial x^{2}}}}.$

(4.47)

Ego resheniem, kak my uzhe otmechali vyshe, yavlyaetsya lyubaya funkciya argumenta $\theta = t \mp x / c$ :

$s(x,t) = s(\theta ) = s\left( {\displaystyle t \mp {\displaystyle \frac{\displaystyle {\displaystyle x}}{\displaystyle {\displaystyle c}}}} \right),$

(4.48)

a skorost' rasprostraneniya volny

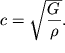$c = \sqrt {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle G}}{\displaystyle {\displaystyle \rho }}}}.$

(4.49)

Processy rasprostraneniya i otrazheniya poperechnyh voln v sterzhne polnost'yu analogichny takovym v odnorodnom natyanutom shnure, poetomu my ih rassmatrivat' ne budem. Skoncentriruem vnimanie na zakonomernostyah perenosa mehanicheskoi energii begushei volnoi.

Energiya, perenosimaya volnoi.

V lekcii po deformaciyam uprugih tverdyh tel my otmechali, chto pri deformacii sdviga v edinice ob'ema tela zapasaetsya potencial'naya energiya

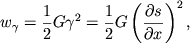$w_{\gamma } = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}G\gamma ^{2} = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}G\left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial x}}}} \right)^{2},$

(4.50)

nazyvaemaya ob'emnoi plotnost'yu energii deformacii sdviga. V (4.50) polagaem $\gamma \approx tg\gamma = {\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial x}}}.$

Pomimo etogo, edinica ob'ema s massoi, ravnoi $\rho,$ i kolebatel'noi skorost'yu $v = \partial s / \partial t$ imeet kineticheskuyu energiyu

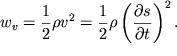$w_{v} = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}\rho v^{2} = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}\rho \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial t}}}} \right)^{2}.$

(4.51)

Polnaya energiya edinicy ob'ema ravna

$w = w_{\gamma } + w_{v} = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}{\displaystyle \left[ {\displaystyle G\left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial x}}}} \right)^{2} + \rho \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial t}}}} \right)^{2}} \right]}.$

(4.52)

Pokazhem, chto v begushei volne (4.48) $w_{\gamma } = w_{v}.$ Dlya etogo vychislim proizvodnye:

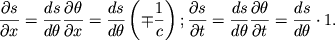${\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial x}}} = {\displaystyle \frac{\displaystyle {\displaystyle ds}}{\displaystyle {\displaystyle d\theta }}}{\displaystyle \frac{\displaystyle {\displaystyle \partial \theta }}{\displaystyle {\displaystyle \partial x}}} = {\displaystyle \frac{\displaystyle {\displaystyle ds}}{\displaystyle {\displaystyle d\theta }}}\left( {\displaystyle \mp {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle c}}}} \right); {\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial t}}} = {\displaystyle \frac{\displaystyle {\displaystyle ds}}{\displaystyle {\displaystyle d\theta }}}{\displaystyle \frac{\displaystyle {\displaystyle \partial \theta }}{\displaystyle {\displaystyle \partial t}}} = {\displaystyle \frac{\displaystyle {\displaystyle ds}}{\displaystyle {\displaystyle d\theta }}} \cdot 1.$

(4.53)

Iz (4.53) poluchaem

${\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial x}}} = \mp {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle c}}} \cdot {\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial t}}},\; ili \; \gamma = \mp {\displaystyle \frac{\displaystyle {\displaystyle v}}{\displaystyle {\displaystyle c}}}.$

(4.54)

Otmetim, chto v begushei volne deformacii $\gamma$ kakogo-libo elementa proporcional'ny ego kolebatel'noi skorosti $v.$

Vozvodya v kvadrat levoe ravenstvo (4.54), delya ego popolam i uchityvaya, chto $c^{2} = G / \rho,$ poluchaem

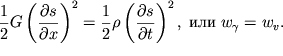${\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}G\left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial x}}}} \right)^{2} = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}\rho \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial t}}}} \right)^{2}, \; ili \; w_{\gamma } = w_{v}.$

(4.55)

Ravenstvo velichin $w_{\gamma }$ i $w_{v}$ pozvolyaet zapisat' polnuyu plotnost' energii w v vide:

$w = 2w_{\gamma } = 2w_{v}.$

(4.56)

Poskol'ku volna dvizhetsya, to ona osushestvlyaet perenos mehanicheskoi energii.

Tak, naprimer, za vremya $\Delta t$ cherez ploshadku edinichnoi ploshadi, zashtrihovannuyu na ris. 4.19, budet perenesena energiya, ravnaya

$\Delta W = wc\Delta t.$

(4.57)

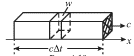Ris. 4.19.

Nazad| Vpered

Publikacii s klyuchevymi slovami: kolebaniya - volny Publikacii so slovami: kolebaniya - volny
Sm. takzhe: Eho iz glubin krasnogo giganta

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce