Astronet > Kolebaniya i volny

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Kolebaniya i volny. Lekcii.

V.A.Aleshkevich, L.G.Dedenko, V.A.Karavaev (Fizicheskii fakul'tet MGU)
Izdatel'stvo Fizicheskogo fakul'teta MGU, 2001 g. Soderzhanie

V fizike ispol'zuyut ponyatie plotnosti potoka energii, opredelyaemoi kolichestvom energii, perenosimoi volnoi za edinicu vremeni cherez edinichnuyu ploshadku, perpendikulyarnuyu napravleniyu rasprostraneniya volny. Soglasno (4.57), eta plotnost' ravna

$J = {\displaystyle \frac{\displaystyle {\displaystyle \Delta W}}{\displaystyle {\displaystyle \Delta t}}} = wc$

(4.58)

i imeet razmernost' [J] = Dzh/(m²*s).

Esli ploshadka imeet ploshad' $dS,$ a ee normal' $\bf n$ sostavlyaet s napravleniem rasprostraneniya volny (os'yu Oh) ugol $\alpha$ (ris. 4.20), to kolichestvo energii, perenosimoe volnoi cherez etu ploshadku za edinicu vremeni (potok energii) raven

$d\Phi = wc \cdot dS\cos \alpha.$

(4.59)

Ris. 4.20.

Professorom MGU N.A. Umovym v 1874 g. byl vveden vektor plotnosti potoka energii

${\displaystyle \bf J} = wc,$

(4.60)

poluchivshii nazvanie vektora Umova. S ego ispol'zovaniem potok $d\Phi$ mozhet byt' zapisan v vide

$d\Phi = {\displaystyle \bf J} \cdot d{\displaystyle \bf S} = JdS\cos \alpha,$

(4.61)

gde $d{\displaystyle \bf S} = dS \cdot {\displaystyle \bf n}.$

S podobnym predstavleniem potoka vektora skorosti my vstrechalis' pri izuchenii dvizheniya zhidkostei.

Udobstvo vektora Umova stanovitsya osobenno oshutimym, kogda volna rasprostranyaetsya v trehmernom prostranstve. Togda potok energii cherez proizvol'nuyu poverhnost' $S$ vyrazhaetsya v vide integrala po etoi poverhnosti:

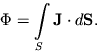$\Phi = {\displaystyle \int\limits_{S} {\displaystyle {\displaystyle \bf J} \cdot d{\displaystyle \bf S}} }.$

(4.62)

Poslednyaya formula budet ispol'zovana nizhe.

Podschitaem srednee znachenie za period vektora Umova dlya begushei vdol' sterzhnya poperechnoi garmonicheskoi volny

$s(x,t) = s_{0} \sin (\omega t - kx).$

(4.63)

Ob'emnaya plotnost' energii (summa potencial'noi i kineticheskoi energii) ravna

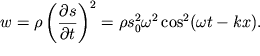$w = \rho \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial t}}}} \right)^{2} = \rho s_{0}^{2} \omega ^{2}\cos ^{2}(\omega t - kx).$

(4.64)

V nekotoryi moment vremeni ona raspredelena vdol' sterzhnya tak, kak pokazano na ris. 4.21. S techeniem vremeni eto raspredelenie smeshaetsya vdol' osi Oh so skorost'yu $s.$ Plotnost' potoka energii cherez lyuboe sechenie x = const budet periodicheski vozrastat' ot nulya do maksimal'noi velichiny $\rho s_{0}^{2} \omega ^{2}.$ Poetomu udobno pol'zovat'sya srednim znacheniem $J$ za period $T = 2\pi / \omega.$ Eta velichina nazyvaetsya intensivnost'yu begushei volny i ravna

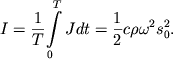$I = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle T}}}{\displaystyle \int\limits_{0}^{T} {\displaystyle Jdt = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}c\rho \omega ^{2}s_{0}^{2}.} }$

(4.65)

Vazhno otmetit', chto intensivnost' proporcional'na kvadratu amplitudy.

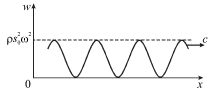Ris. 4.21.

V stoyachei volne net perenosa energii, t. k. ona yavlyaetsya superpoziciei dvuh begushih voln, perenosyashih odinakovoe kolichestvo energii v protivopolozhnyh napravleniyah. Odnako, lokal'noe dvizhenie energii v ogranichennom prostranstve mezhdu sosednimi uzlami vse zhe proishodit. V samom dele, zapishem uravnenie stoyachei volny (4.34), opustiv v nem postoyannye fazovye dobavki $\varphi _{otr} / 2 i k\ell$ :

$s(x,t) = 2s_{0} \cos kx\sin \omega t.$

(4.66)

Ob'emnaya plotnost' energii deformacii sdviga ravna:

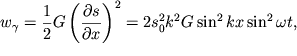$w_{\gamma } = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}G\left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial x}}}} \right)^{2} = 2s_{0}^{2} k^{2}G\sin ^{2}kx\sin ^{2}\omega t,$

(4.67)

a ob'emnaya plotnost' kineticheskoi energii vyrazhaetsya kak:

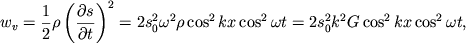$w_{v} = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}\rho \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial t}}}} \right)^{2} = 2s_{0}^{2} \omega ^{2}\rho \cos ^{2}kx\cos ^{2}\omega t = 2s_{0}^{2} k^{2}G\cos ^{2}kx\cos ^{2}\omega t,$

(4.68)

poskol'ku 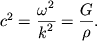$c^{2} = {\displaystyle \frac{\displaystyle {\displaystyle \omega ^{2}}}{\displaystyle {\displaystyle k^{2}}}} = {\displaystyle \frac{\displaystyle {\displaystyle G}}{\displaystyle {\displaystyle \rho }}}.$

Lokal'noe dvizhenie energii naglyadno demonstriruet ris. 4.22, na kotorom pokazan fragment stoyachei volny v momenty vremeni $t_{1} = 0$ i $t_{2} = t_{1} + T / 4$ (a) i sootvetstvuyushie raspredeleniya $w_{\gamma }$ (b) i $w_{v}$ (v).

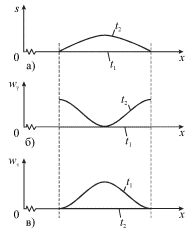Ris. 4.22.

Vidno, chto pri $t = t_{1},$ kogda elementy sterzhnya prohodyat polozhenie ravnovesiya i imeyut maksimal'nye skorosti, deformaciya otsutstvuet $(w_{\gamma } = 0),$ a vsya energiya zapasena v vide kineticheskoi energii $w_{v}$ i lokalizovana vblizi puchnosti. Odnako cherez chetvert' perioda kolebanii chasticy sterzhnya smestyatsya na maksimal'nye rasstoyaniya i ostanovyatsya $(w_{v} = 0).$ Energiya budet zapasena v vide potencial'noi energii $w_{\gamma }$ i lokalizovana vblizi uzlov. Eto oznachaet, chto energiya iz oblasti vblizi puchnosti za chetvert' perioda kolebanii peretekaet v obe storony po napravleniyu k uzlam. Zatem ona dvizhetsya v obratnom napravlenii, i etot process povtoryaetsya mnogokratno. Potok energii cherez uzly otsutstvuet. Srednee za period znachenie potoka energii cherez lyuboe sechenie x = const budet ravno nulyu $(I = 0).$

Prodol'nye volny.

Takie volny mogut byt' vozbuzhdeny udarom molotka po odnomu iz torcov uprugogo sterzhnya. Vozmushenie, rasprostranyayusheesya vdol' sterzhnya, vizual'no nezametno, odnako osnovnye zakonomernosti takogo volnovogo processa mozhno smodelirovat', esli vmesto sterzhnya ispol'zovat' dlinnuyu pruzhinu s bol'shim diametrom vitkov (ris. 4.23). Esli etu pruzhinu podvesit' gorizontal'no na neskol'kih nityah (ne pokazannyh na risunke) i rezko udarit' ladon'yu po levomu torcu, to po nei pobezhit impul's szhatiya s nekotoroi skorost'yu $c.$ Na ris. 4.23a etot impul's imeet dlinu $c\tau _{i}$ ( $\tau _{i}$ - dlitel'nost' impul'sa, ravnaya dlitel'nosti udara). Dobezhav do pravogo konca pruzhiny, on otrazitsya, pri etom, esli konec zakreplen (ris. 4.23b), to otrazhennyi impul's budet takzhe impul'som szhatiya. Esli pravyi konec svoboden, to otrazhennyi impul's budet impul'som rastyazheniya (ris. 4.23v). On voznikaet v moment smesheniya vpravo svobodnogo konca pruzhiny, kogda do nego dobezhit impul's szhatiya. Eta situaciya napominaet smeshenie svobodnogo konca shnkrv. Otmetim, chto v rassmotrennom sluchae smesheniya vitkov pruzhiny proishodyat vdol' napravleniya rasprostraneniya volny, poetomu volna nazyvaetsya prodol'noi.

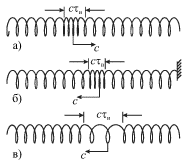Ris. 4.23.

Rassmotrim teper' rasprostranenie impul'sov szhatiya i rastyazheniya v sterzhne.

Myslenno razob'em sterzhen' na ryad elementov dlinoi $dx$ kazhdyi. Pri rasprostranenii prodol'noi volny koncy kazhdogo elementa, otmechennye na ris. 4.24 sploshnymi liniyami, budut smesheny v novye polozheniya, otmechennye punktirom. Eti smesheniya s budem schitat' polozhitel'nymi, esli oni proishodyat v polozhitel'nom napravlenii osi Oh, i otricatel'nymi - v protivopolozhnom sluchae.

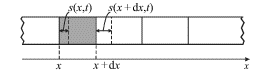Ris. 4.24.

Pust' levyi konec nekotorogo elementa, imeyushii koordinatu h, smestilsya v dannyi moment vremeni $t$ na rasstoyanie $s(x,t),$ a pravyi konec - na $s(x + dx,t).$ Deformaciya rastyazheniya (szhatiya) opredelyaetsya otnositel'nym udlineniem elementa $dx$ :

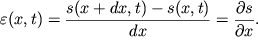$\varepsilon (x,t) = {\displaystyle \frac{\displaystyle {\displaystyle s(x + dx,t) - s(x,t)}}{\displaystyle {\displaystyle dx}}} = {\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial x}}}.$

(4.69)

Otmetim, deformacii rastyazheniya sootvetstvuet $\varepsilon \gt 0,$ a szhatiya - $\varepsilon \lt 0.$

V otlichie ot poperechnoi volny, pri rastyazhenii (szhatii) umen'shaetsya (uvelichivaetsya) plotnost' sredy $\rho.$ Ee mozhno predstavit' v vide

$\rho = \rho _{0} + \delta \rho ; \vert \delta \rho \vert \ll \rho _{0}.$

(4.70)

Zdes' $\delta \rho$ - malaya dobavka k ravnovesnoi plotnosti $\rho _{0},$ prichem $\delta \rho$ mozhet byt' kak polozhitel'noi, tak i otricatel'noi. S uchetom postoyanstva massy deformiruemogo elementa $dx$ mozhem zapisat'

$\rho _{0} dx = (\rho _{0} + \delta \rho )[dx + s(x + dx,t) - s(x,t)] = (\rho _{0} + \delta \rho )dx(1 + \varepsilon ).$

(4.71)

Raskryvaya skobki i prenebregaya maloi velichinoi $\varepsilon \cdot \delta \rho,$ nahodim

${\displaystyle \frac{\displaystyle {\displaystyle \delta \rho }}{\displaystyle {\displaystyle \rho _{0} }}} = - \varepsilon.$

(4.72)

Spustya nekotoroe vremya $t$ posle udara po torcu sterzhnya (ili posle rezkogo ottyagivaniya etogo torca) raspredelenie smeshenii $s,$ deformacii $\varepsilon$ i vozmushenii plotnosti $\delta \rho$ v begushih impul'sah szhatiya i rastyazheniya budut imet' vid, pokazannyi na ris. 4.25. Punktirom pokazany raspredeleniya vseh velichin v odin iz posleduyushih momentov vremeni.

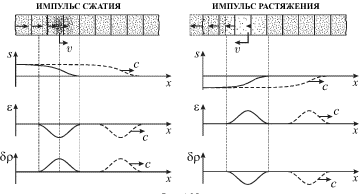Ris. 4.25.

Uravnenie volny, begushei vdol' osi Oh, v oboih sluchayah imeet vid $s(x,t) = s(t - x / c).$ Po analogii s (4.54) deformaciya $\varepsilon = \partial s / \partial x$ i kolebatel'naya skorost' $v = \partial s / \partial t$ elementa svyazany sootnosheniem

${\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial x}}} = - {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle c}}}{\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial t}}}, \; ili \; \varepsilon = - {\displaystyle \frac{\displaystyle {\displaystyle v}}{\displaystyle {\displaystyle c}}}.$

(4.73)

Podcherknem, chto v impul'se szhatiya $(\varepsilon \lt 0)$ skorost' $v$ sovpadaet po napravleniyu so skorost'yu $s,$ a v impul'se rastyazheniya oni imeyut protivopolozhnye napravleniya.

Rasschitaem skorost' rasprostraneniya prodol'nyh voln. Na ris. 4.26 izobrazhen fragment sterzhnya i pokazan ego element $dx,$ k koncam kotorogo prilozheny normal'nye napryazheniya $\sigma _{n}.$ Uravnenie dvizheniya elementa s poperechnym secheniem ravnym $S$ imeet vid:

$dm{\displaystyle \frac{\displaystyle {\displaystyle \partial ^{2}s}}{\displaystyle {\displaystyle \partial t^{2}}}} = S{\displaystyle \left[ {\displaystyle \sigma _{n} (x + dx,t) - \sigma _{n} (x,t)} \right]},$

(4.74)

gde $dm = \rho _{0} Sdx.$ Chtoby (4.74) preobrazovat' k volnovomu uravneniyu, neobhodimo svyazat' napryazheniya $\sigma _{n}$ s deformaciyami elementov sterzhnya. Naibolee prosto eto mozhno sdelat' dlya tonkogo sterzhnya.

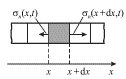Ris. 4.26.

Skorost' voln v tonkom sterzhne.

Esli sterzhen' tonkii, to deformacii i napryazheniya vdol' koordinaty h svyazany izvestnym zakonom Guka:

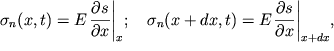$\sigma _{n} (x,t) = E{\displaystyle \left. {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial x}}}} \right|}_{x} ; \quad \sigma _{n} (x + dx,t) = E{\displaystyle \left. {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial x}}}} \right|}_{x + dx},$

(4.75)

gde $E$ - modul' Yunga.

Podstavlyaya (4.75) v (4.74) i proizvodya delenie na $\rho _{0} Sdx,$ poluchaem volnovoe uravnenie:

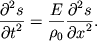${\displaystyle \frac{\displaystyle {\displaystyle \partial ^{2}s}}{\displaystyle {\displaystyle \partial t^{2}}}} = {\displaystyle \frac{\displaystyle {\displaystyle E}}{\displaystyle {\displaystyle \rho _{0} }}}{\displaystyle \frac{\displaystyle {\displaystyle \partial ^{2}s}}{\displaystyle {\displaystyle \partial x^{2}}}}.$

(4.76)

Skorost' prodol'nyh voln poluchaetsya ravnoi

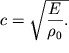$c = \sqrt {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle E}}{\displaystyle {\displaystyle \rho _{0} }}}.}$

(4.77)

Eta skorost' prevyshaet skorost' poperechnyh voln (sm. formulu (4.49)), poskol'ku $E \gt G.$ Po poryadku velichiny obe skorosti sovpadayut i dlya razlichnyh materialov preimushestvenno lezhat v diapazone $c\sim (10^{3}\div 10^{4}) m/c.$

Nazad| Vpered

Publikacii s klyuchevymi slovami: kolebaniya - volny Publikacii so slovami: kolebaniya - volny
Sm. takzhe: Eho iz glubin krasnogo giganta

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce