Astronet > Kolebaniya i volny

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Kolebaniya i volny. Lekcii.

V.A.Aleshkevich, L.G.Dedenko, V.A.Karavaev (Fizicheskii fakul'tet MGU)
Izdatel'stvo Fizicheskogo fakul'teta MGU, 2001 g. Soderzhanie

Skorost' voln v tolstom sterzhne.

Pust' vdol' osi tolstogo sterzhnya (osi h) rasprostranyaetsya prodol'naya volna, pri etom koleblyutsya elementy sterzhnya, nahodyashiesya vblizi ego osi.

Odin iz takih elementov pokazan na ris. 4.27. Pod deistviem normal'nogo napryazheniya $\sigma _{1}$ otnositel'noe udlinenie $\varepsilon _{1}$ opredelyaetsya pervym uravneniem (1.27), privedennym v lekcii po deformacii tverdogo tela:

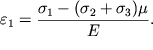$\varepsilon _{1} = {\displaystyle \frac{\displaystyle {\displaystyle \sigma _{1} - (\sigma _{2} + \sigma _{3} )\mu }}{\displaystyle {\displaystyle E}}}.$

(4.78)

Eto uravnenie otrazhaet tot fakt, chto pri udlinenii elementa $dx,$ izobrazhennogo na ris. 4.27, ploshad' ego poperechnogo secheniya umen'shaetsya (svyaz' prodol'noi i poperechnoi deformacii opredelyaetsya koefficientom Puassona $0 \lt \mu \lt 1 / 2$ ). Etot element potyanet k osi sterzhnya okruzhayushie ego elementy, razvivaya napryazheniya $\sigma _{2}$ i $\sigma _{3}.$ Eti elementy (lezhashie mezhdu ploskostyami x = const i x + dx = const) nachnut prihodit' v dvizhenie: snachala - nahodyashiesya vblizi osi sterzhnya, a zatem i elementy, blizkie k poverhnosti. 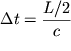Cherez vremya $\Delta t = {\displaystyle \frac{\displaystyle {\displaystyle L / 2}}{\displaystyle {\displaystyle c}}}$ ( $L$ - poperechnyi razmer sterzhnya, s - skorost' rasprostraneniya vozmusheniya) vse elementy smestyatsya, i napryazheniya $\sigma _{2}$ i $\sigma _{3}$ ischeznut.

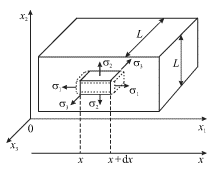Ris. 4.27.

Esli dlitel'nost' $\tau _{i}$ impul'sa, rasprostranyayushegosya vdol' osi sterzhnya, velika, tak chto $\tau _{i} \gg \Delta t = {\displaystyle \frac{\displaystyle {l}}{\displaystyle {\displaystyle 2c}}},$ to v (4.78) mozhno ne uchityvat' $\sigma _{2}$ i $\sigma _{3}.$ Skorost' takogo dlinnogo impul'sa budet opredelyat'sya formuloi (4.77). Takoi rezhim mozhno realizovat', esli

$L \ll c\tau _{i}.$

(4.79)

Uslovie (4.79) oznachaet, chto poperechnyi razmer sterzhnya $L$ znachitel'no men'she dliny impul'sa. Takoi sterzhen' mozhno schitat' tonkim. Esli rech' idet o garmonicheskoi volne, rasprostranyayusheisya vdol' sterzhnya, to uslovie (4.79) imeet vid

$L \ll \lambda,$

(4.80)

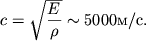gde $\lambda = cT$ - dlina volny, $T$ - period kolebanii. Tak, naprimer, dlya stal'nogo sterzhnya $c = \sqrt {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle E}}{\displaystyle {\displaystyle \rho }}}} \sim 5000 m/s.$ Pri chastote $\nu = 5000 Gc,\; \lambda = c / \nu \sim 1 m,$ poetomu sterzhni s poperechnym razmerom $L\sim 1 sm$ mogut schitat'sya tonkimi.

Esli dlitel'nosti impul'sa $\tau _{i} \ll \Delta t = {\displaystyle \frac{\displaystyle {l}}{\displaystyle {\displaystyle 2c}}}$ (sterzhen' tolstyi), to v (4.78) sleduet uchest' $\sigma _{2}$ i $\sigma _{3}$ . Chtoby naiti svyaz' $\varepsilon _{1}$ i $\sigma _{1},$ vmeste s uravneniem (4.78) zapishem analogichnye dlya $\varepsilon _{2}$ i $\varepsilon _{3}$ i slozhim vse tri uravneniya:

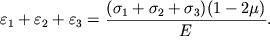$\varepsilon _{1} + \varepsilon _{2} + \varepsilon _{3} = {\displaystyle \frac{\displaystyle {\displaystyle (\sigma _{1} + \sigma _{2} + \sigma _{3} )(1 - 2\mu )}}{\displaystyle {\displaystyle E}}}.$

(4.81)

Dlya kratkosti vykladok vvedem srednie znacheniya

$\varepsilon = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 3}}}(\varepsilon _{1} + \varepsilon _{2} + \varepsilon _{3} ); \quad \sigma = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 3}}}(\sigma _{1} + \sigma _{2} + \sigma _{3} ).$

Togda (4.81) perepishetsya v vide

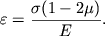$\varepsilon = {\displaystyle \frac{\displaystyle {\displaystyle \sigma (1 - 2\mu )}}{\displaystyle {\displaystyle E}}}.$

(4.82)

S uchetom (4.82) uravnenie (4.78) vidoizmenyaetsya:

$\varepsilon _{1} + {\displaystyle \frac{\displaystyle {\displaystyle 3\mu \varepsilon }}{\displaystyle {\displaystyle 1 - 2\mu }}} = {\displaystyle \frac{\displaystyle {\displaystyle 1 + \mu }}{\displaystyle {\displaystyle E}}}\sigma _{1}.$

(4.83)

Esli polozhit' v tolstom sterzhne $\varepsilon _{2} = \varepsilon _{3} = 0,$ to $\varepsilon = \varepsilon _{1} / 3,$ i iskomaya svyaz' poluchitsya v vide:

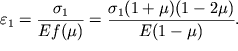$\varepsilon _{1} = {\displaystyle \frac{\displaystyle {\displaystyle \sigma _{1} }}{\displaystyle {\displaystyle Ef(\mu )}}} = {\displaystyle \frac{\displaystyle {\displaystyle \sigma _{1} (1 + \mu )(1 - 2\mu )}}{\displaystyle {\displaystyle E(1 - \mu )}}}.$

(4.84)

V etom sluchae svyaz' deformacii i napryazheniya opredelyaetsya kak modulem Yunga $E,$ tak i sleduyushei funkciei koefficienta Puassona

$f(\mu ) = {\displaystyle \frac{\displaystyle {\displaystyle 1 - \mu }}{\displaystyle {\displaystyle (1 + \mu )(1 - 2\mu )}}}.$

(4.85)

Legko ubedit'sya, chto pri lyubyh vozmozhnyh znacheniyah koefficienta Puassona $f(\mu ) \gt 1.$ Poetomu skorost' prodol'noi volny v etom sluchae

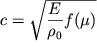$c = \sqrt {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle E}}{\displaystyle {\displaystyle \rho _{0} }}}f(\mu )}$

(4.86)

prevyshaet skorost' volny v tonkom sterzhne. Velichinu $E \cdot f(\mu )$ obychno nazyvayut "modulem odnostoronnego rastyazheniya".

Otmetim, chto naibolee slozhen analiz dlya promezhutochnogo sluchaya, kogda $L\sim \lambda.$ Dlya voln s takoi dlinoi volny imeet mesto dispersiya (fazovaya skorost' garmonicheskoi volny zavisit ot ee chastoty). Raspredelenie amplitudy volny v poperechnom sechenii sterzhnya vdol' osei $x_{2}$ i $x_{3}$ analogichno raspredeleniyu amplitudy dlya shnura dlinoi $L$ so svobodnymi koncami pri normal'nom kolebanii. Sterzhen' v etom sluchae vypolnyaet rol' volnovoda. Pri ego plavnom izgibanii volna rasprostranyaetsya vdol' ego osi.

Prodol'nye volny perenosyat energiyu, i dlya nih spravedlivy vse rassuzhdeniya i vyvody, poluchennye dlya poperechnyh voln. Formal'no vo vse vyrazheniya dlya plotnosti energii $w,$ vektora Umova $\bf J$ i dr. sleduet vmesto modulya sdviga $G$ podstavit' modul' Yunga $E$ ili $E \cdot f(\mu ).$ Predostavlyaem chitatelyu prodelat' eto samostoyatel'no.

Yavleniya na granice dvuh sred.

Rassmotrim podrobnee prohozhdenie prodol'noi volny cherez granicu razdela dvuh uprugih sred pri normal'nom padenii volny na etu granicu.

Pust' prodol'naya volna rasprostranyaetsya so skorost'yu $c_{1} = \sqrt {\displaystyle E_{1} / \rho _{1} }$ v srede s modulem Yunga $E_{1}$ i ravnovesnoi plotnost'yu $\rho _{1}$ (ris. 4.28). Opyt pokazyvaet, chto eta volna na granice razdela dvuh sred ( $h = 0$ na risunke) chastichno otrazhaetsya i chastichno prohodit vo vtoruyu sredu, kotoraya harakterizuetsya parametrami $E_{2}$ i $\rho _{2}.$ Sledovatel'no, mozhem zapisat'

1-ya sreda	2-ya sreda	(4.87)
(padayushaya + otrazhennaya volna)	(proshedshaya volna)
$s_{1} (x,t) = s_{01} \sin (\omega t - k_{1} x) + {\displaystyle s}'_{01} \sin (\omega t + k_{1} x)$	$s_{2} (x,t) = s_{02} \sin (\omega t - k_{2} x)$

Zdes' $\omega$ - chastota, $s_{01}, {\displaystyle s}'_{01}$ i $s_{02}$ - amplitudy padayushei, otrazhennoi i proshedshei voln sootvetstvenno, $k_{1} = \omega / c_{1}$ i $k_{2} = \omega / c_{2}$ - sootvetstvuyushie volnovye chisla.

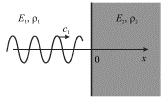Ris. 4.28.

Chtoby naiti sootnosheniya mezhdu amplitudami treh voln, opredelyayushie otrazhatel'nuyu i propuskatel'nuyu sposobnost' ("prozrachnost'") granicy razdela, zapishem dva usloviya, kotorye dolzhny vypolnyat'sya na granice razdela pri $h = 0.$

Pervoe - eto uslovie nerazryvnosti veshestva:

$s_{1} (0,t) = s_{2} (0,t).$

(4.88)

Vtoroe - ravenstvo napryazhenii:

$\sigma _{1} (0,t) = \sigma _{2} (0,t), \; ili \; E_{1} \varepsilon _{1} (0,t) = E_{2} \varepsilon _{2} (0,t).$

(4.89)

S uchetom (4.87) iz etih uslovii poluchaem:

$\begin{array}{l} s_{01} + {\displaystyle s}'_{01} = s_{02}, \\ - s_{01} E_{1} k_{1} + {\displaystyle s}'_{01} E_{1} k_{1} = - s_{02} E_{2} k_{2}. \\ \end{array}$

(4.90)

V akustike fundamental'nym yavlyaetsya ponyatie impedansa, ili udel'nogo volnovogo (akusticheskogo) soprotivleniya materiala. Eta velichina $z$ opredelyaetsya kak:

$z = {\displaystyle \frac{\displaystyle {\displaystyle szhimayushee\; napryazhenie}}{\displaystyle {\displaystyle kolebatel'naya\; skorost'}} = {\displaystyle \frac{\displaystyle {\displaystyle - \sigma }}{\displaystyle {\displaystyle v}}}}.$

(4.91)

Impedans legko mozhno vyrazit' cherez harakteristiki materiala, vospol'zovavshis' formuloi (4.73):

$\varepsilon = {\displaystyle \frac{\displaystyle {\displaystyle \sigma }}{\displaystyle {\displaystyle E}}} = - {\displaystyle \frac{\displaystyle {\displaystyle v}}{\displaystyle {\displaystyle c}}}.$

(4.92)

Otsyuda

$z = {\displaystyle \frac{\displaystyle {\displaystyle - \sigma }}{\displaystyle {\displaystyle v}}} = {\displaystyle \frac{\displaystyle {\displaystyle E}}{\displaystyle {\displaystyle c}}} = \rho c.$

(4.93)

S ispol'zovaniem etoi velichiny i vyrazhenii dlya $k_{1}$ i $k_{2}$ usloviya (4.90) primut vid:

$\begin{array}{l} s_{01} + {\displaystyle s}'_{01} = s_{02} \\ - s_{01} z_{1} + {\displaystyle s}'_{01} z_{1} = - s_{02} z_{2}. \\ \end{array}$

(4.94)

Otsyuda poluchaem iskomuyu svyaz' mezhdu amplitudami voln:

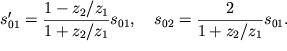${\displaystyle s}'_{01} = {\displaystyle \frac{\displaystyle {\displaystyle 1 - z_{2} / z_{1} }}{\displaystyle {\displaystyle 1 + z_{2} / z_{1} }}}s_{01}, \quad s_{02} = {\displaystyle \frac{\displaystyle {\displaystyle 2}}{\displaystyle {\displaystyle 1 + z_{2} / z_{1} }}}s_{01}.$

(4.95)

Dlya prakticheskih celei pol'zuyutsya koefficientami otrazheniya $R$ i propuskaniya $T,$ harakterizuyushimi otnoshenie intensivnostei otrazhennoi i proshedshei voln k intensivnosti padayushei volny. Eti koefficienty poluchayutsya iz (4.95) s uchetom (4.65):

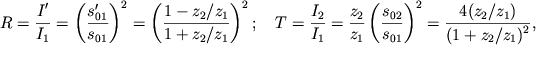$R = {\displaystyle \frac{\displaystyle {\displaystyle {\displaystyle I}'}}{\displaystyle {\displaystyle I_{1} }}} = \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle {\displaystyle s}'_{01} }}{\displaystyle {\displaystyle s_{01} }}}} \right)^{2} = \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle 1 - z_{2} / z_{1} }}{\displaystyle {\displaystyle 1 + z_{2} / z_{1} }}}} \right)^{2}; \quad T = {\displaystyle \frac{\displaystyle {\displaystyle I_{2} }}{\displaystyle {\displaystyle I_{1} }}} = {\displaystyle \frac{\displaystyle {\displaystyle z_{2} }}{\displaystyle {\displaystyle z_{1} }}}\left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle s_{02} }}{\displaystyle {\displaystyle s_{01} }}}} \right)^{2} = {\displaystyle \frac{\displaystyle {\displaystyle 4(z_{2} / z_{1} )}}{\displaystyle {\displaystyle (1 + z_{2} / z_{1} )^{2}}}},$

(4.96)

gde ispol'zovano to obstoyatel'stvo, chto intensivnost' begushei volny (sm. formulu (4.65))

$I = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}c\rho \omega ^{2}s_{0}^{2} = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}z\omega ^{2}s_{0}^{2}$

(4.97)

zavisit ne tol'ko ot amplitudy $s_{0}$ i chastoty $\omega,$ no i proporcional'na akusticheskomu soprotivleniyu $z.$ Sleduet otmetit', chto formuly (4.96) spravedlivy i dlya poperechnyh kolebanii.

Iz risunka 4.29, na kotorom izobrazheny zavisimosti (4.96), vidno, chto esli $z_{1} = z_{2},$ otrazheniya ne proishodit. Poetomu na praktike, kogda nado umen'shit' otrazhenie, starayutsya soglasovat' (sdelat' prakticheski odinakovymi) volnovye soprotivleniya dvuh sred.

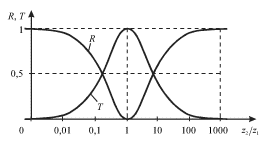Ris. 4.29.

Zametim takzhe, chto pri $z_{2} \ll z_{1},$ kak v sluchae svobodnogo konca sterzhnya ( $z_{2}$ - soprotivlenie vozduha), ili $z_{2} \gg z_{1}$ (zakreplennyi konec), $R \approx 1,$ t.e. proishodit prakticheski polnoe otrazhenie volny, chto my i ispol'zovali vyshe pri rassmotrenii otrazheniya v etih predel'nyh sluchayah.

Nazad| Vpered

Publikacii s klyuchevymi slovami: kolebaniya - volny Publikacii so slovami: kolebaniya - volny
Sm. takzhe: Eho iz glubin krasnogo giganta

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce