Astronet > Kolebaniya i volny

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Kolebaniya i volny. Lekcii.

V.A.Aleshkevich, L.G.Dedenko, V.A.Karavaev (Fizicheskii fakul'tet MGU)
Izdatel'stvo Fizicheskogo fakul'teta MGU, 2001 g. Soderzhanie

Akusticheskie fonony. Ob'emnye seismicheskie volny. Sovremennaya model' Zemli. Volny Releya i Lyava. Volny v zhidkostyah i gazah. Zvuk. Intensivnost' zvuka. Pogloshenie zvuka. Izluchateli zvuka. Primenenie akusticheskih metodov. Osnovnye harakteristiki zvuka. Zakon Vebera-Fehnera. Diagramma sluha. Akusticheskie rezonatory. Muzykal'nye instrumenty. Effekt Doplera i binaural'nyi effekt. Interferenciya i difrakciya voln.

Teplovye kolebaniya kristallicheskoi reshetki tverdyh tel. Akusticheskie fonony.

V tverdom tele iony sovershayut teplovye kolebaniya okolo polozhenii ravnovesiya v uzlah kristallicheskoi reshetki. Poskol'ku oni vzaimodeistvuyut drug s drugom, to sistema ionov dolzhna rassmatrivat'sya kak sovokupnost' svyazannyh oscillyatorov. Takie teplovye kolebaniya ionov mozhno predstavit' v vide superpozicii stoyachih zvukovyh voln, chastoty kotoryh $\omega$ lezhat v diapazone $0 \lt \omega \le \omega _{N},$ gde $\omega _{N}$ - maksimal'naya chastota kolebanii, obuslovlennaya diskretnost'yu sredy (sm. predydushuyu lekciyu).

Pri nagrevanii kristalla energiya teplovyh kolebanii uvelichivaetsya. Estestvenno, chto informaciyu ob etih kolebaniyah mozhno poluchit', izmeryaya teploemkost' kristallov.

Esli kazhdyi ion rassmatrivat' kak klassicheskii oscillyator, koleblyushiisya v treh vzaimno perpendikulyarnyh napravleniyah, to, v sootvetstvii s teoremoi o ravnoraspredelenii energii po stepenyam svobody, on obladal by energiei $\varepsilon _{1} = 6kT / 2,$ gde $k$ - postoyannaya Bol'cmana, a $T$ - absolyutnaya temperatura. Zdes' uchteno, chto koleblyushiisya ion obladaet srednei kineticheskoi i ravnoi ei srednei potencial'noi energiei $kT/2$ po kazhdoi iz treh stepenei svobody. Poskol'ku energiya kristalla, sostoyashego iz $N$ atomov, $U = N\varepsilon _{1} = 3NkT,$ to ego teploemkost' pri postoyannom ob'eme ravna:

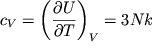$c_{V} = \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \partial U}}{\displaystyle {\displaystyle \partial T}}}} \right)_{V} = 3Nk$

(5.1)

i ne zavisit ot temperatury (zakon Dyulonga i Pti).

Mezhdu tem, formula (5.1) soglasuetsya s eksperimentom lish' pri vysokih temperaturah, a pri priblizhenii temperatury k absolyutnomu nulyu, kak pokazyvaet opyt, $c_{V} \sim T^{3}.$

Chtoby ob'yasnit' takoe povedenie teploemkosti, A. Einshtein predlozhil rassmatrivat' iony kak nezavisimye oscillyatory, obladayushie diskretnym naborom znachenii energii. Ranee podobnaya ideya byla vyskazana M. Plankom pri vyvode formuly dlya teplovogo izlucheniya tverdogo tela. Odnako, A. Einshteinu ne udalos' poluchit' zakon $T^{3}.$

Na samom dele, kak uzhe govorilos', teplovye kolebaniya ionov mogut byt' predstavleny kak superpoziciya normal'nyh kolebanii, ili mod sistemy svyazannyh oscillyatorov. Kazhdaya moda chastoty $\omega$ obladaet energiei, kratnoi $\hbar \omega,$ gde $\hbar = h / 2\pi$ ( $h = 6,67 \cdot 10^{ - 34} Dzh/s$ - postoyannaya Planka).

Esli prinyat' vo vnimanie, chto v tverdom tele vozmozhno rasprostranenie prodol'noi volny chastoty $\omega$ i dvuh poperechnyh voln toi zhe chastoty, imeyushih dva razlichnyh vzaimno perpendikulyarnyh napravleniya smesheniya atomov (dve razlichnye polyarizacii), to s uchetom razmerov kristalla i ego diskretnoi struktury mozhno podschitat' chislo mod v kristalle. Takoi podschet byl vpervye vypolnen P. Debaem, i poetomu eti volny poluchili nazvanie debaevskih.

Sleduet podcherknut', chto, v otlichie ot klassicheskogo predstavleniya, pri vychislenii energii kristalla moda predstavlyaetsya kak kvantovyi ob'ekt, obladayushii diskretnym naborom znachenii energii (naborom energeticheskih urovnei)

$\varepsilon _{n} = n\hbar \omega,$

(5.2)

gde $n$ - celoe chislo.

Pri termodinamicheskom ravnovesii veroyatnost' $\cal P}_{n$ vozbuzhdeniya mody ubyvaet po mere uvelicheniya ee energii $\varepsilon _{n}$ (ili chisla $n$ ) v sootvetstvii s raspredeleniem Bol'cmana: ${\displaystyle \cal P}_{n} \sim e^{ - n\hbar \omega / kT}.$ Pri nagrevanii kristalla veroyatnost' $\cal P}_{n$ rastet, a znachit uvelichivaetsya i zapasennaya kristallom energiya. Pri podschete poslednei Debaem byla vvedena harakternaya temperatura (temperatura Debaya) $\theta _{D}$ s pomosh'yu ravenstva

$k\theta _{D} = \hbar \omega _{N}.$

(5.3)

Obychno $\theta _{D}$ lezhit v intervale $(10^{2}\div 10^{3}) K.$ Pri $T \gg \theta _{D}$ spravedliv zakon Dyulonga i Pti, a pri $T \ll \theta _{D}$ teploemkost' $c_{V} \sim T^{3}.$

Sootnoshenie (5.2) dlya energii kolebanii v mode chastoty $\omega$ analogichno vyrazheniyu dlya energii fotonov (kvantov sveta). Eto pozvolyaet rassmatrivat' modu kak kvazichasticu, nazyvaemuyu teplovym fononom. Vvedenie etogo novogo ponyatiya yavlyaetsya ves'ma plodotvornym i, s matematicheskoi tochki zreniya, znachitel'no oblegchaet analiz teplovyh kolebanii kristallicheskoi reshetki. Predstavlenie o fononnom gaze v tverdom tele shiroko ispol'zuetsya pri opisanii takih svoistv, kak teploemkost', teploprovodnost', teplovoe rasshirenie, elektricheskoe soprotivlenie i dr. V fizike ispol'zuyutsya i drugie kvazichasticy: plazmon (volna elektronnoi plotnosti), magnon (volna peremagnichivaniya), polyaron (elektron + uprugaya deformaciya), eksiton (volna polyarizacii sredy). Eti kvazichasticy yavlyayutsya modami sootvetstvuyushih kolebanii.

Ob'emnye seismicheskie volny.

Chrezvychaino vazhnym primerom voln v uprugom tverdom tele yavlyayutsya seismicheskie volny, voznikayushie v ogranichennoi oblasti prostranstva (ochage) razmerom v neskol'ko kilometrov i rasprostranyayushiesya na ogromnye rasstoyaniya pod poverhnost'yu Zemli. Eti volny byvayut poperechnymi (volny sdviga) i prodol'nymi (szhatiya i razrezheniya) i mogut pronizyvat' vsyu nashu planetu. Eto pozvolyaet (podobno rentgenovskomu analizu) issledovat' vnutrennee stroenie Zemli. Etim zanimaetsya otdel'naya nauka, nazyvaemaya seismologiei. Dolgoe vremya seismologiya, odnim iz osnovatelei kotoroi yavlyaetsya russkii fizik B.B. Golicyn, byla naukoi o zemletryaseniyah i seismicheskih volnah. V nastoyashee vremya seismologiya zanimaetsya analizom raznoobraznyh dvizhenii v zemnoi tolshe.

Skorost' prodol'nyh voln priblizitel'no v 1,7 raza bol'she skorosti poperechnyh, poetomu eti volny registriruyutsya na seismogrammah posledovatel'no: vnachale prihodyat bolee bystrye prodol'nye (pervichnye), kotorye nazyvayutsya r-volnami, a potom poperechnye (vtorichnye), nazyvaemye s-volnami. Krome togo, seismografy registriruyut i zametnyi fon, ili shumy, svyazannye kak s rabotoi promyshlennyh ustanovok i transporta, tak i s seismicheskimi volnami (mikroseismami), generiruemymi shtormami i volneniem v okeanah.

Esli by skorosti r- i s-voln v Zemle ne menyalis' by s glubinoi, to volny rasprostranyalis' by po pryamym liniyam (pryamym seismicheskim lucham). V deistvitel'nosti skorosti prodol'noi $c_{p}$ i poperechnoi $c_{s}$ voln vozrastayut s pogruzheniem v nedra Zemli, za isklyucheniem nebol'shoi zony na glubinah 50-250 km. Poetomu seismicheskie luchi iskrivlyayutsya. V seismologii eksperimental'no opredelyayut godograf - vremya $\tau$ probega seismicheskih voln kak funkciyu epicentral'nogo rasstoyaniya $\Delta$ (rasstoyaniya v gradusah ili kilometrah po duge bol'shogo kruga mezhdu epicentrom i priemnikom voln; $1^\circ = 111 km$ ). Yasno, chto funkciya $\tau = \tau (\Delta )$ svyazana s raspredeleniem skorosti volny $c(\ell )$ ( $\ell$ - glubina), i poisk etogo raspredeleniya predstavlyaet interes pri issledovanii vnutrennego stroeniya Zemli.

Na ris. 5.1 pokazany puti p-voln i ukazano vremya ih rasprostraneniya v nedrah Zemli ot epicentra E do ustanovlennogo na poverhnosti priemnika. Preryvistye linii (izohrony) ukazyvayut vremya prihoda p-voln v razlichnye tochki zemnoi poverhnosti. Iz-za iskrivleniya luchei volny ne popadayut v obshirnuyu zonu teni.

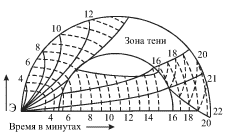Ris. 5.1.

Issledovanie zavisimosti skorostei $c_{p} (\ell )$ i $c_{s} (\ell )$ ot glubiny pozvolilo sdelat' vyvod, chto Zemlya razdelyaetsya na tri osnovnye chasti: koru, mantiyu i yadro. Kora otdelena ot mantii rezkoi seismicheskoi granicei, na kotoroi skachkoobrazno vozrastayut plotnost' $\rho$ i skorosti $c_{p}$ i $c_{s}.$ Eta granica byla otkryta v 1909 g. yugoslavskim seismologom Mohorovichichem i nosit nazvanie granicy M. Tolshina lezhashei vyshe granicy M zemnoi kory menyaetsya ot velichiny $\approx 10 km$ ( pod sloem vody v okeanicheskih oblastyah) do neskol'kih desyatkov kilometrov v gornyh raionah kontinental'nyh oblastei. Nizhe kory v intervale do glubin ~ 2900 km raspolozhena silikatnaya obolochka, ili mantiya Zemli. Sushestvovanie yadra s plotnost'yu, prevoshodyashei srednyuyu plotnost' Zemli ~ 5,5 g/sm^³, sleduet iz togo fakta, chto plotnost' zemnoi kory (ot ~ 2,8 g/sm³ u granitov do ~ 3,0 g/sm³ u bazal'tov) sushestvenno men'she etoi srednei plotnosti.

Na ris. 5.2 pokazany glubinnye zavisimosti skorostei r- i s-voln i na baze etih zavisimostei provedeno razbienie Zemli na tri oblasti. Takaya model' Zemli nazyvaetsya klassicheskoi model'yu Dzheffrisa-Gutenberga. Ona ostavalas' neizmennoi do konca 60-h godov HH veka. Osobennosti izmeneniya skorostei voln s glubinoi svyazany s izmeneniem struktury zemnyh porod. Pri perehode ot kory (granity, bazal'ty) k mantii (ul'traosnovnye gornye porody) skorosti vozrastayut. Uvelichenie skorostei pri priblizhenii k yadru svyazano s nalichiem fazovyh perehodov mineralov v bolee plotnye i zhestkie v mehanicheskom otnoshenii kristallicheskie modifikacii. Padenie skorosti r-voln pri perehode iz mantii v yadro est' sledstvie togo, chto vneshnyaya chast' yadra zhidkaya. Yadro sostoit v osnovnom iz zheleza i nebol'shoi primesi legkih elementov. Vo vneshnem yadre plavnoe vozrastanie skorosti $c_{p}$ svyazano s narastaniem davleniya k centru Zemli. Vo vnutrennem yadre skorost' p-voln ne menyaetsya, tak kak davlenie k centru Zemli vozrastaet neznachitel'no. Estestvenno, chto poperechnye s-volny vo vneshnei (zhidkoi) chasti yadra rasprostranyat'sya ne mogut.

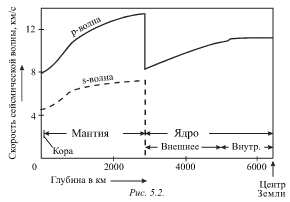Ris. 5.2.

Nazad| Vpered

Publikacii s klyuchevymi slovami: kolebaniya - volny Publikacii so slovami: kolebaniya - volny
Sm. takzhe: Eho iz glubin krasnogo giganta

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

Kolebaniya i volny. Lekcii.

Lekciya 5

Teplovye kolebaniya kristallicheskoi reshetki tverdyh tel. Akusticheskie fonony.

Ob'emnye seismicheskie volny.