Astronet > Kolebaniya i volny

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Kolebaniya i volny. Lekcii.

V.A.Aleshkevich, L.G.Dedenko, V.A.Karavaev (Fizicheskii fakul'tet MGU)
Izdatel'stvo Fizicheskogo fakul'teta MGU, 2001 g. Soderzhanie

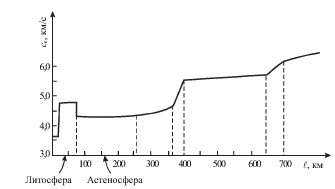
V poslednie gody byla vyyavlena detal'naya struktura mantii Zemli. Na ris. 5.3 pokazano raspredelenie skorosti $c_{s} (\ell )$ v mantii, iz kotorogo mozhno sdelat' zaklyuchenie o ee strukture. Zemnaya kora i verhnii sloi mantii do glubiny $\ell \approx 70 km$ obrazuyut naruzhnuyu zonu - litosferu, ili litosfernuyu plitu. Eta zhestkaya plita raskolota primerno na 10 bol'shih plit, po granicam kotoryh raspolozheno podavlyayushee chislo ochagov zemletryasenii. Pod zhestkoi litosfernoi plitoi na glubinah $70 \lt \ell \lt 250 km$ raspolozhen sloi povyshennoi tekuchesti, nazyvaemyi astenosferoi. Iz-za ee maloi vyazkosti $(\mu \sim 10^{20}\div 10^{21} Puaz)$ litosfernye plity kak by plavayut v "astenosfernom okeane" Zemli. V astenosfere, gde temperatura veshestva blizka k temperature plavleniya, skorosti voln ponizheny. Nachinaya s $\ell \approx 250 km$ skorosti vozrastayut iz-za uvelicheniya davleniya. Pri $\ell \approx 400 km$ vozrastanie skorosti est' rezul'tat fazovyh perehodov (mineraly oliviny perehodyat v shpinelevuyu modifikaciyu), a na glubinah $400 \lt \ell \lt 650 km$ skorost' vozrastaet iz-za rosta davleniya. Na glubinah $650 \lt \ell \lt 700 km$ raspolozhena vtoraya zona fazovyh perehodov, odnako ostaetsya otkrytym vopros o tom, kakie konkretno perehody otvetstvenny za bystryi rost skorosti.

Ris. 5.3.

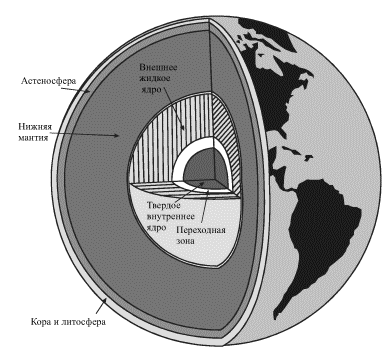
Na ris. 5.4 izobrazhen razrez Zemli, postroennyi v sootvetstvii s sovremennymi seismicheskimi dannymi.

Ris. 5.4.

Pri rasprostranenii ob'emnoi seismicheskoi volny v trehmernom sluchae amplituda umen'shaetsya s rasstoyaniem r, proidennym volnoi ot tochechnogo istochnika. Uravnenie takoi volny, nazyvaemoi sfericheskoi, imeet vid:

$s(r,t) = {\displaystyle \frac{\displaystyle {\displaystyle s_{0} }}{\displaystyle {\displaystyle r}}}e^{ - \alpha r}\sin {\displaystyle \left[ {\displaystyle \omega \left( {\displaystyle t - {\displaystyle \frac{\displaystyle {\displaystyle r}}{\displaystyle {\displaystyle c}}}} \right)} \right]}.$

(5.4)

Iz etogo uravneniya vidno, chto amplituda volny ubyvaet, vo-pervyh, iz-za ee geometricheskogo rashozhdeniya vo vse storony ot epicentra; eto ubyvanie proishodit obratno proporcional'no proidennomu volnoi rasstoyaniyu $r.$ Vo-vtoryh, amplituda volny ubyvaet iz-za perehoda chasti energii volny v teplo vsledstvie neideal'noi uprugosti zemnyh nedr. Eto oslablenie harakterizuetsya koefficientom zatuhaniya $\alpha.$ Koefficient $\alpha$ proporcionalen chastote seismicheskoi volny, poetomu korotkie volny zatuhayut bystree dlinnyh. Raschet pokazyvaet, chto dlya koefficientov zatuhaniya s- i p-voln mogut byt' zapisany sootnosheniya

$\alpha _{s} (km^{-1}) \sim 1 \cdot 10^{ - 3}\nu (Gc);\quad \alpha _{p} (km^{-1}) \sim 0,25 \cdot 10^{ -3}\nu (Gc)$

Chastoty ob'emnyh seismicheskih voln lezhat v infrazvukovom diapazone $0,1 Gc \lt \nu \lt10 Gc.$ Sledovatel'no, dlya voln s chastotoi $\nu \sim 1 Gc$ umen'shenie amplitudy v e raz u poperechnoi volny proishodit na puti ~ 1000 km, a u prodol'noi volny - na puti ~ 4000 km.

Pomimo begushih voln, v ob'eme Zemli mogut nablyudat'sya i stoyachie volny, kogda vsya Zemlya kolebletsya, kak celoe, s razlichnymi chastotami, sootvetstvuyushimi razlichnym modam kolebanii. Konfiguracii etih mod otnosyatsya k dvum osnovnym tipam: sferoidal'nye kolebaniya (naibol'shii period ~ 55 min., chastota ~ 3*10^-4 Gc) i torsionnye (krutil'nye) kolebaniya (naibol'shii period ~ 44 min., chastota ~ 3,8*10^-4 Gc). V nastoyashee vremya spektr etih kolebanii naschityvaet neskol'ko tysyach eksperimental'no obnaruzhennyh chastot.

Poverhnostnye seismicheskie volny.

Naryadu s ob'emnymi, po Zemle mogut rasprostranyatsya i poverhnostnye volny. Eti volny byvayut dvuh tipov i nazyvayutsya volnami Releya i Lyava. Oni byli teoreticheski predskazany Dzh. Releem v 1855 g. i Lyavom v 1911 g. V Releevskoi volne chasticy grunta smeshayutsya v vertikal'noi ploskosti, orientirovannoi vdol' napravleniya rasprostraneniya voln, a traektorii ih dvizheniya predstavlyayut soboi ellipsy (sm. dalee gravitacionnye volny na poverhnosti zhidkosti). V volne Lyava chasticy dvizhutsya v gorizontal'noi ploskosti poperek napravleniya rasprostraneniya volny.

Dliny poverhnostnyh voln $\lambda,$ vozbuzhdaemyh pri zemletryasenii, lezhat v intervale ot desyatkov do mnogih soten kilometrov. V poverhnostnyh volnah amplituda ubyvaet s glubinoi, i na glubine $\ell \gt \lambda$ kolebaniya mantii maly. Poetomu s pomosh'yu takih voln mozhno issledovat' lish' naruzhnye sloi Zemli.

Iz-za dvumernogo rasprostraneniya amplituda poverhnostnyh voln ubyvaet medlennee (obratno proporcional'no $\sqrt {\displaystyle r}$ ), chem u ob'emnyh voln. Poetomu takie volny mogut po neskol'ko raz obegat' vokrug zemnogo shara. Skorost' poverhnostnyh voln zavisit ot chastoty, t. e. oni obladayut dispersiei.

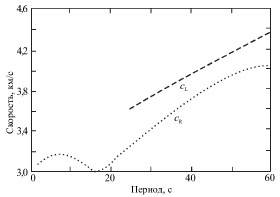
Na risunke 5.5 pokazany zavisimosti gruppovyh skorostei voln Releya $c_{R}$ i Lyava $c_{L}$ ot perioda kolebaniya volny. Legko videt', chto volny Lyava rasprostranyayutsya bystree voln Releya. Otmetim, chto na ris. 5.5 pokazany $c_{R}$ i $c_{L}$ lish' dlya voln, amplitudy kotoryh opredelennym obrazom ubyvayut s glubinoi. Vozmozhny poverhnostnye volny i s drugimi raspredeleniyami amplitud po glubine.

Ris. 5.5.

Seismicheskie volny mozhno vyzvat' pri pomoshi vzryva. Nebol'shie vzryvy ispol'zuyutsya v inzhenernoi seismologii dlya provedeniya razvedki poleznyh iskopaemyh (nefti, rudy, gaza i t. d.). Podzemnye yadernye vzryvy sozdayut intensivnye volny, kotorye mozhno registrirovat' na lyubyh rasstoyaniyah. Eto daet vozmozhnost' nadezhno provodit' kontrol' nad podzemnymi yadernymi ispytaniyami.

Volny v zhidkostyah i gazah.

V zhidkostyah i gazah vozmozhny lish' deformacii szhatiya i rastyazheniya, poetomu v nih mogut rasprostranyatsya tol'ko prodol'nye volny. Hotya my ranee i rasschityvali skorost' rasprostraneniya vozmushenii v gaze, tem ne menee vychislim skorost' rasprostraneniya prodol'nyh voln s ispol'zovaniem volnovogo uravneniya. Poslednee mozhet byt' polucheno iz (4.74), v kotorom $\sigma _{n}$ sleduet zamenit' velichinoi $- \delta p = p_{0} - p,$ gde $r$ - davlenie v volne, $p_{0}$ - ravnovesnoe davlenie v srede, $\delta p$ - vozmushenie davleniya. Togda my mozhem zapisat'

$dm{\displaystyle \frac{\displaystyle {\displaystyle \partial ^{2}s}}{\displaystyle {\displaystyle \partial t^{2}}}} = [ - \delta p(x + dx,t) + \delta p(x,t)]S.$

(5.5)

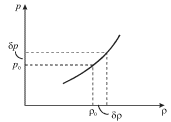
Chtoby iz (5.5) poluchit' volnovoe uravnenie, neobhodimo znat' material'noe uravnenie sredy

$p = p(\rho ).$

(5.6)

Kachestvenno eta zavisimost' izobrazhena na ris. 5.6. Pri ochen' malyh vozmusheniyah plotnosti $\left| {\displaystyle \delta \rho } \right| \ll \rho _{0}$ i davleniya $\left| {\displaystyle \delta p} \right| \ll p_{0}$ iz (5.6) poluchaem:

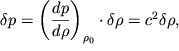$\delta p = \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle dp}}{\displaystyle {\displaystyle d\rho }}}} \right)_{\rho _{0} } \cdot \delta \rho = c^{2}\delta \rho,$

(5.7)

gde vvedeno oboznachenie

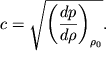$c = \sqrt {\displaystyle \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle dp}}{\displaystyle {\displaystyle d\rho }}}} \right)_{\rho _{0} } }.$

(5.8)

Ris. 5.6.

S uchetom (4.69) i (4.72) vozmusheniya plotnosti $\delta \rho$ v (5.7) svyazany so smesheniem s sootnosheniem:

$\delta \rho = - \varepsilon \rho _{0} = - \rho _{0} {\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial x}}}.$

(5.9)

Sledovatel'no, (5.7) primet vid:

$\delta p = - \rho _{0} c^{2}{\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial x}}}.$

(5.10)

Podstavlyaya (5.10) v (5.5), zapisyvaya $dm = \rho _{0} Sdx$ i perehodya k predelu pri $dx \to 0,$ poluchim volnovoe uravnenie

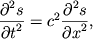${\displaystyle \frac{\displaystyle {\displaystyle \partial ^{2}s}}{\displaystyle {\displaystyle \partial t^{2}}}} = c^{2}{\displaystyle \frac{\displaystyle {\displaystyle \partial ^{2}s}}{\displaystyle {\displaystyle \partial x^{2}}}},$

(5.11)

iz kotorogo srazu vidno, chto skorost' volny zadaetsya vyrazheniem (5.8) i ne zavisit ot chastoty (dispersiya otsutstvuet). Estestvenno, chto s takoi skorost'yu rasprostranyayutsya volny s dlinoi volny $\lambda,$ prevoshodyashei dlinu svobodnogo probega molekul v gaze ili mezhatomnye rasstoyaniya v zhidkostyah $\ell.$ V etom sluchae zhidkost' i gaz mogut rassmatrivat'sya kak sploshnye sredy. Dlya voln vysokih chastot, kogda $\lambda \sim \ell,$ voznikaet dispersiya, a volny s dlinoi $\lambda \lt \ell$ rasprostranyat'sya voobshe ne mogut.

Uprugie volny v zhidkostyah i gazah, kak, vprochem, i v tverdyh telah, nazyvayutsya akusticheskimi, a razdel fiziki, kotoryi ih izuchaet - akustikoi. Chastoty etih voln lezhat v diapazone ot dolei gerca (infrazvuk) do 10¹³ Gc (giperzvuk). Etim chastotam sootvetstvuyut dliny voln $\lambda$ ot desyatkov kilometrov do neskol'kih angstrem. Znacheniya skorostei (fazovyh i gruppovyh) dlya raznyh sred lezhat v diapazone ot dolei do desyatkov km/s.

Dlya vozduha material'noe uravnenie (5.6) yavlyaetsya uravneniem adiabaty i v akustike obychno zapisyvaetsya v vide (sm. takzhe predydushie lekcii):

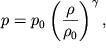$p = p_{0} \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \rho }}{\displaystyle {\displaystyle \rho _{0} }}}} \right)^{\gamma },$

(5.12)

gde $\gamma = c_{p} / c_{V}$ - pokazatel' adiabaty.

Togda iz (5.8) skorost' volny (v akustike upotreblyayut termin "skorost' zvuka") v gaze poluchaetsya ravnoi

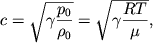$c = \sqrt {\displaystyle \gamma {\displaystyle \frac{\displaystyle {\displaystyle p_{0} }}{\displaystyle {\displaystyle \rho _{0} }}}} = \sqrt {\displaystyle \gamma {\displaystyle \frac{\displaystyle {\displaystyle RT}}{\displaystyle {\displaystyle \mu }}}},$

(5.13)

gde $\mu$ - molyarnaya massa gaza.

Skorost' zvuka zavisit, takim obrazom, ot roda gaza i po poryadku velichiny sovpadaet so srednei skorost'yu teplovogo dvizheniya molekul.

Dlya zhidkosti material'nym uravneniem yavlyaetsya poluempiricheskoe uravnenie Teta:

$p = p_{vn} {\displaystyle \left[ {\displaystyle \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \rho }}{\displaystyle {\displaystyle \rho _{0} }}}} \right)^{\Gamma } - 1} \right]},$

(5.14)

gde $p_{vn}$ - harakternoe vnutrennee davlenie, obuslovlennoe mezhmolekulyarnym vzaimodeistviem (ono sostavlyaet dlya bol'shinstva zhidkostei bez puzyr'kov i razlichnyh vklyuchenii neskol'ko tysyach atmosfer). Parametr $\Gamma$ imeet poryadok neskol'kih edinic (naprimer, dlya vody $\Gamma \approx 7$ ).

V tablice privedeny znacheniya skorosti zvuka, izmerennye v nekotoryh gazah (pri temperature $t = 0^\circ C$ ) i zhidkostyah.

Gazy	Skorost' zvuka, m/s	Zhidkosti	Skorost' zvuka, m/s
Vodorod	1265	Voda $(t = 20^\circ C)$	1490
Gelii	965	Etil. spirt $(t = 20^\circ C)$	1180
Azot	334	Vodorod $(t = -252^\circ C)$	1127
Vozduh	331	Kislorod $(t = -183^\circ C)$	911
Kislorod	316	Azot $(t = -196^\circ C)$	867
Uglekislota	216	Gelii $(t = -269^\circ C)$	180

Nazad| Vpered

Publikacii s klyuchevymi slovami: kolebaniya - volny Publikacii so slovami: kolebaniya - volny
Sm. takzhe: Eho iz glubin krasnogo giganta

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce