Astronet > Kolebaniya i volny

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Kolebaniya i volny. Lekcii.

V.A.Aleshkevich, L.G.Dedenko, V.A.Karavaev (Fizicheskii fakul'tet MGU)
Izdatel'stvo Fizicheskogo fakul'teta MGU, 2001 g. Soderzhanie

Energiya, perenosimaya zvukovoi volnoi.

Intensivnost' zvuka zadaetsya formuloi (4.65)

$I = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}c\rho _{0} \omega ^{2}s_{0}^{2}$

(5.15)

i proporcional'na kvadratu chastoty. Poetomu pri perehode v oblast' vysokih chastot oblegchaetsya zadacha polucheniya bol'shih intensivnostei, neobhodimyh, naprimer, dlya nablyudeniya nelineinyh effektov (sm. sleduyushuyu lekciyu). V zavisimosti ot reshaemoi zadachi v akustike ispol'zuyutsya volny s intensivnost'yu ot 10^-8 Vt/sm² do 10⁶ Vt/sm².

Dlya prakticheskih celei intensivnost' $I$ vyrazhayut cherez vozmushenie davleniya $\delta p,$ kotoroe nazyvayut takzhe "zvukovym davleniem". Naibolee prosto takuyu zavisimost' mozhno poluchit' iz (5.15) pri uchete, chto amplituda skorosti kolebanii chastic $v_{0} = \omega s_{0}.$ S drugoi storony, v sootvetstvii s akusticheskim zakonom Oma (formula (3.53) v lekcii po mehanike sploshnyh sred) eta skorost' ravna

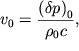$v_{0} = {\displaystyle \frac{\displaystyle {\displaystyle \left( {\displaystyle \delta p} \right)_{0} }}{\displaystyle {\displaystyle \rho _{0} c}}},$

(5.16)

gde $\left( {\displaystyle \delta p} \right)_{0}$ - amplituda kolebanii vozmushenii davleniya $\delta p.$ Poetomu

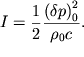$I = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}{\displaystyle \frac{\displaystyle {\displaystyle \left( {\displaystyle \delta p} \right)_{0}^{2} }}{\displaystyle {\displaystyle \rho _{0} c}}}.$

(5.17)

Vypolnim nekotorye prostye ocenki.

1. Vblizi strui gaza, vytekayushei iz sopla reaktivnogo dvigatelya samoleta, amplituda kolebanii zvukovogo davleniya $(\delta p)_{0} = 300 Pa$ (vspomnim, chto $p_{0} = 10^{5} Pa$ i $\left( {\displaystyle \delta p} \right)_{0} \ll p_{0}.$ Takoe davlenie nahoditsya na poroge bolevogo oshusheniya (sm. dalee). Poskol'ku akusticheskoe volnovoe soprotivlenie vozduha $z = \rho _{0} c = 41 sm^{-2} \cdot s^{-1},$ to $v_{0} = 73 sm/s.$ Esli prinyat', chto chastota $\nu = 10^{3} Gc$ (hotya iz turbiny ishodit mnogochastotnyi shum), to amplituda smesheniya $s_{0} = v_{0} / 2\pi \nu = 0,01 sm.$ Takim obrazom, smeshenie chastic vozduha dazhe pri takom sil'nom zvuke okazyvaetsya malym.

2. Zvuki na predele slyshimosti na chastote $\nu = 10^{3} Gc$ (uho cheloveka ves'ma chuvstvitel'no k etoi chastote) imeyut amplitudu zvukovogo davleniya $(\delta p)_{0} = 2 \cdot 10^{ - 5} Pa,$ a smeshenie chastic vozduha $s_{0} = 0,8 \cdot 10^{ - 9} sm.$ Umestno zametit', chto sovremennye metody izmereniya smeshenii v principe dayut vozmozhnost' zaregistrirovat' kolebaniya s amplitudoi $s_{0} \sim 10^{ - 16} sm.$

3. V ul'trazvukovyh volnah s chastotami poryadka neskol'kih megagerc intensivnosti mogut dostigat' neskol'kih soten Vt/sm², a s ispol'zovaniem fokusiruyushih ustroistv - dazhe bolee desyatka kVt/sm². Eto privodit k poyavleniyu ogromnyh uskorenii chastic sredy, v kotoroi rasprostranyaetsya ul'trazvukovaya volna. Naprimer, pri rasprostranenii v vode volny s chastotoi $\nu = 10^{6} Gc$ i intensivnost'yu $I = 100 Vt/sm^{2}$ amplituda uskoreniya $a_{0} = \omega ^{2}s_{0},$ soglasno (5.15), poluchaetsya ravnoi

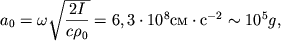$a_{0} = \omega \sqrt {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle 2I}}{\displaystyle {\displaystyle c\rho _{0} }}}} = 6,3 \cdot 10^{8} sm \cdot s^{-2} \sim 10^{5}g,$

(5.18)

chto na pyat' poryadkov prevoshodit uskorenie svobodnogo padeniya $g.$ Uchet poyavleniya takih gromadnyh uskorenii osobenno vazhen v biologicheskih issledovaniyah s primeneniem ul'trazvuka.

Pogloshenie zvuka.

Nalichie vyazkosti i teploprovodnosti sredy privodit k potere energii zvukovoi volny, i eta energiya rashoduetsya na nagrevanie sredy. Volna davleniya $\delta p({\displaystyle \bf r},t),$ a takzhe volny smesheniya $s({\displaystyle \bf r},t)$ i skorosti $v({\displaystyle \bf r},t) = \partial s / \partial t$ po mere rasprostraneniya zatuhayut. Zdes' $\bf r$ - radius-vektor, zadayushii polozhenie tochki v trehmernom prostranstve, v kotoroi fiksiruyutsya vozmusheniya davleniya, smeshenie chastic i ih skorost'. V sluchae garmonicheskoi volny, rasprostranyayusheisya po odnomu napravleniyu (vdol' osi Ox), vozmusheniya davleniya zapisyvayutsya v vide

$\delta p(x,t) = (\delta p)_{0} e^{ - \alpha x}\sin {\displaystyle \left[ {\displaystyle \omega \left( {\displaystyle t - {\displaystyle \frac{\displaystyle {\displaystyle x}}{\displaystyle {\displaystyle c}}}} \right)} \right]},$

(5.19)

gde $\alpha$ - koefficient zatuhaniya. Eto uravnenie harakterizuet ploskuyu volnu (vozmushenie $\delta p$ v ploskosti x = const odinakovo). V etom sluchae otsutstvuet geometricheskoe rashozhdenie volny. Amplituda etoi volny $(\delta p)_{0} e^{ - \alpha x}$ eksponencial'no ubyvaet s proidennym rasstoyaniem. V sootvetstvii s (5.17) intensivnost' volny ravna

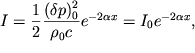$I = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}{\displaystyle \frac{\displaystyle {\displaystyle (\delta p)_{0}^{2} }}{\displaystyle {\displaystyle \rho _{0} c}}}e^{ - 2\alpha x} = I_{0} e^{ - 2\alpha x},$

(5.20)

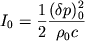gde $I_{0} = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}{\displaystyle \frac{\displaystyle {\displaystyle (\delta p)_{0}^{2} }}{\displaystyle {\displaystyle \rho _{0} c}}}$ - nachal'naya intensivnost' volny. Esli prenebrech' poteryami, svyazannymi s teploprovodnost'yu, to koefficient $\alpha,$ soglasno gidrodinamike, okazyvaetsya ravnym

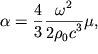$\alpha = {\displaystyle \frac{\displaystyle {\displaystyle 4}}{\displaystyle {\displaystyle 3}}}{\displaystyle \frac{\displaystyle {\displaystyle \omega ^{2}}}{\displaystyle {\displaystyle 2\rho _{0} c^{3}}}}\mu,$

(5.21)

gde $\mu$ - vyazkost' zhidkosti ili gaza. Vazhno otmetit', chto $\alpha \sim \omega ^{2}.$ Etim ob'yasnyaetsya tot fakt, chto rezkii zvuk vystrela ili shelchka knuta, v spektre kotorogo prisutstvuet shirokii nabor chastot, po mere rasprostraneniya transformiruetsya v bolee myagkii, poskol'ku v spektre ostayutsya preimushestvenno nizkie chastoty. Zametim, chto pogloshenie zvuka v vode sushestvenno men'she, chem v vozduhe, a v tverdyh telah eshe men'she, chem v vode. Ochen' nizkim poglosheniem zvuka otlichayutsya takie kristally, kak sapfir, topaz, berill, niobat litiya i drugie.

V zaklyuchenie otmetim, chto pogloshenie zvuka yavlyaetsya glavnym prepyatstviem, ogranichivayushim primenenie mnogih materialov na vysokih chastotah.

Izluchateli zvuka.

Primenyaemye v akustike izluchateli uprugih voln mozhno podrazdelit' na dve bol'shie gruppy.

K pervoi otnosyatsya izluchateli-generatory; kolebaniya v nih vozbuzhdayutsya iz-za nalichiya prepyatstviya na puti postoyannogo potoka gaza ili zhidkosti (sireny, svistki, generatory Gartmana). Takie generatory primenyayutsya v osnovnom v diapazone chastot do $30\div 40 kGc.$ Oni otlichayutsya vysokim koefficientom preobrazovaniya kineticheskoi energii strui v akusticheskuyu (do 50%), prostotoi konstrukcii i ekspluatacii, desheviznoi. Intensivnost' zvuka v neposredstvennoi blizosti ot izluchatelya mozhet dostigat' 10 Vt/sm². K nedostatkam etih izluchatelei otnosyatsya shirokii spektr izluchaemyh chastot, nestabil'nost' izluchaemoi moshnosti, nevozmozhnost' polucheniya zvukovyh kolebanii zadannoi formy.

Vtoruyu gruppu izluchatelei sostavlyayut elektroakusticheskie preobrazovateli. Svoe nazvanie oni poluchili ottogo, chto preobrazuyut elektricheskie kolebaniya v mehanicheskie kolebaniya kakogo-libo tverdogo tela, kotoroe i izluchaet v okruzhayushuyu sredu akusticheskie volny. Naibolee rasprostranennye elektroakusticheskie preobrazovateli, takie, kak elektrodinamicheskie izluchateli, magnitostrikcionnye i p'ezoelektricheskie preobrazovateli, predstavlyayut soboi lineinye ustroistva, blagodarya chemu oni vozbuzhdayut akusticheskuyu volnu toi zhe formy, chto i elektricheskii signal. Krome togo, eti ustroistva obratimy, to est' mogut rabotat' i kak izluchateli, i kak priemniki zvuka.

V diapazone slyshimyh chastot shirokoe rasprostranenie poluchili elektrodinamicheskie izluchateli, princip deistviya kotoryh osnovan na vzaimodeistvii peremennogo elektricheskogo toka s magnitnym polem (telefony, gromkogovoriteli). V magnitostrikcionnyh preobrazovatelyah ispol'zuetsya effekt magnitostrikcii - deformacii tverdogo tela v magnitnom pole.

V ul'trazvukovom i giperzvukovom diapazonah (do 10¹⁰ Gc) naibolee shiroko primenyayutsya p'ezoelektricheskie preobrazovateli, princip deistviya kotoryh osnovan na obratnom p'ezoeffekte - deformacii tela pod deistviem elektricheskogo polya.

Na ris. 5.7 shematichno pokazan prosteishii preobrazovatel', osnovu kotorogo sostavlyaet p'ezoplastinka, vyrezannaya special'nym obrazom iz monokristalla kvarca, niobata litiya (LiNbO₃) ili drugogo p'ezomateriala. K protivopolozhnym poverhnostyam plastinki (obychno metallizirovannym ili pokrytym metallicheskimi elektrodami) prikladyvaetsya peremennoe napryazhenie $U$ s chastotoi $\nu.$ Tolshina plastinki $\ell$ budet pri etom periodicheski izmenyat'sya s toi zhe chastotoi, prichem eto izmenenie ne prevoshodit neskol'kih mikron. Vibriruyushie poverhnosti plastinki privodyat v dvizhenie soprikasayushiisya s nimi vozduh. Naibol'shaya amplituda kolebanii budet pri rezonanse, kogda na tolshine $\ell$ ukladyvaetsya nechetnoe chislo poluvoln:

$\ell = n{\displaystyle \frac{\displaystyle {\displaystyle \lambda _{n} }}{\displaystyle {\displaystyle 2}}}; n = 1, 3, 5 \ldots$

(5.22)

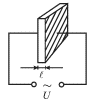Ris. 5.7.

Otmetim, chto pri chetnom $n$ na elektrodah voznikli by elektricheskie zaryady odnogo znaka, chto nevozmozhno. Rezonansnye chastoty poluchayutsya ravnymi

$\nu _{n} = {\displaystyle \frac{\displaystyle {\displaystyle c}}{\displaystyle {\displaystyle \lambda _{n} }}} = {\displaystyle \frac{\displaystyle {\displaystyle nc}}{\displaystyle {\displaystyle 2\ell }}}.$

(5.23)

Naprimer, dlya p'ezokvarca pri skorosti prodol'nyh voln $c = 5700 m/s$ i tolshine plastinki $\ell = 1 mm$ rezonansnye chastoty ravny

$\nu _{n} = n \cdot 2850 kGc.$

(5.24)

Naibol'shuyu amplitudu kolebanii imeet volna osnovnoi chastoty $(n = 1),$ poetomu p'ezoizluchateli primenyayutsya, kak pravilo, na osnovnoi chastote.

Na chastotah do neskol'kih megagerc shirokoe rasprostranenie poluchili preobrazovateli iz p'ezokeramiki. P'ezokeramika predstavlyaet soboi polikristallicheskii segnetoelektricheskii material (tverdye rastvory na osnove BaTiO₃-CaTiO₃, PbTiO₃-PbZnO₃ i drugie), obladayushii posle polyarizacii v elektricheskom pole ustoichivymi i sil'nymi p'ezoelektricheskimi svoistvami. Iz p'ezokeramiki mozhno izgotavlivat' izluchateli samoi raznoi formy (v vide plastin, sterzhnei, kolec i tak dalee). S pomosh'yu preobrazovatelei sfericheskoi ili cilindricheskoi formy poluchayut sfokusirovannyi ul'trazvukovoi puchok, v fokuse kotorogo intensivnost' zvuka dostigaet $10^{5}\div 10^{6} Vt/sm^{2}.$

Na chastotah poryadka desyatkov i soten megagerc tolshina $\ell$ stanovitsya nastol'ko maloi, chto izgotovit' preobrazovatel' mozhno lish' v zhestkom soedinenii so zvukoprovodom - massivnym kuskom zvukoprovodyashego materiala. V etom sluchae na horosho otpolirovannuyu poverhnost' zvukoprovoda napylyaetsya metallicheskaya plenka (odin elektrod), k kotoroi privarivaetsya tolstaya (poryadka 1 mm) plastinka p'ezoelektrika. Zatem eta plastinka soshlifovyvaetsya do nuzhnoi tolshiny $\ell,$ posle chego na nee nanositsya vtoroi elektrod.

Na chastotah poryadka 1 GGc tolshina p'ezopreobrazovatelya sostavlyaet $\ell \sim 1 mkm.$ Izgotovlenie takih preobrazovatelei predstavlyaet ser'eznuyu tehnologicheskuyu problemu. V etom chastotnom diapazone primenyayutsya plenochnye preobrazovateli, poluchaemye napyleniem na torec zvukoprovoda p'ezoelektricheskih plenok iz takih materialov, kak CdS, ZnS, ZnO i drugie. Sovremennye tehnologii pozvolyayut sozdavat' preobrazovateli s koefficientom preobrazovaniya elektricheskoi energii v akusticheskuyu do 90% i moshnost'yu volny, dostigayushei neskol'kih vatt.

Nazad| Vpered

Publikacii s klyuchevymi slovami: kolebaniya - volny Publikacii so slovami: kolebaniya - volny
Sm. takzhe: Eho iz glubin krasnogo giganta

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce