Astronet > Kolebaniya i volny

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Kolebaniya i volny. Lekcii.

V.A.Aleshkevich, L.G.Dedenko, V.A.Karavaev (Fizicheskii fakul'tet MGU)
Izdatel'stvo Fizicheskogo fakul'teta MGU, 2001 g. Soderzhanie

Garmonicheskie kolebaniya (1.7) dopuskayut naglyadnuyu graficheskuyu interpretaciyu. Ee smysl sostoit v tom, chto kazhdomu garmonicheskomu kolebaniyu s chastotoi $\omega _{0}$ mozhno postavit' v sootvetstvie vrashayushiisya s uglovoi skorost'yu $\omega _{0}$ vektor, dlina kotorogo ravna amplitude $s_{0},$ a ego nachal'noe (startovoe) polozhenie zadaetsya uglom $\varphi _{0},$ sovpadayushim s nachal'noi fazoi (ris. 1.5).

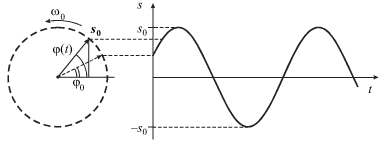Ris. 1.5.

Vertikal'naya proekciya vektora $\bf s_{0}$ izmenyaetsya so vremenem: $s(t) = s_{0} \sin \varphi (t).$ Mgnovennoe polozhenie vektora $\bf s_{0}$ opredelyaetsya uglom $\varphi (t),$ kotoryi nazyvaetsya fazoi i raven:

$\varphi (t) = \omega _{0} t + \varphi _{0} .$

(1.18)

Pri uglovoi skorosti (krugovoi chastote) $\omega _{0}$ vektor sovershaet $\nu _{0} = \omega _{0} / 2\pi$ oborotov (ciklov) v sekundu, a prodolzhitel'nost' odnogo oborota (period) ravna otnosheniyu ugla $2\pi$ k uglovoi skorosti $\omega _{0} :\; T = 2\pi / \omega _{0} .$

S pomosh'yu vektornyh diagramm legko osushestvit' slozhenie garmonicheskih kolebanii. Tak, esli neobhodimo slozhit' dva garmonicheskih kolebaniya s odinakovymi chastotami

$s(t) = s_{1} (t) + s_{2} (t) = s_{01} \sin (\omega _{0} t + \varphi _{1} ) + s_{02} \sin (\omega _{0} t + \varphi _{2} ) = s_{0} \sin (\omega _{0} t + \varphi _{0} ),$

to amplitudu $s_{0}$ i nachal'nuyu fazu $\varphi _{0}$ summarnogo kolebaniya $s(t)$ s toi zhe chastotoi $\omega _{0}$ mozhno legko rasschitat' iz ris. 1.6a, na kotorom graficheski izobrazhena operaciya slozheniya vektorov $\bf s_{0}} = {\displaystyle \bf s_{01}} + {\displaystyle \bf s_{02}$ v moment vremeni $t = 0:$

$s_{0} = \sqrt {\displaystyle (s_{01} \cos \varphi _{1} + s_{02} \cos \varphi _{2} )^{2} + (s_{01} \sin \varphi _{1} + s_{02} \sin \varphi _{2} )^{2}},$

$\varphi _{0} = {\rm arctg\,}{\displaystyle \frac{\displaystyle {\displaystyle s_{01} \sin \varphi _{1} + s_{02} \sin \varphi _{2} }}{\displaystyle {\displaystyle s_{01} \cos \varphi _{1} + s_{02} \cos \varphi _{2} }}}.$

Yasno, chto vertikal'naya proekciya vektora $\bf s_{0}$ budet takzhe izmenyat'sya po garmonicheskomu zakonu s chastotoi $\omega _{0},$ poskol'ku vzaimnoe raspolozhenie vektorov $s_{01}$ i $s_{02}$ ne izmenyaetsya s techeniem vremeni.

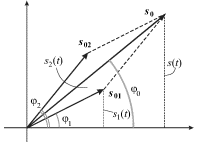Ris. 1.6a.

Iz etoi diagrammy naglyadno vidno, chto summarnoe kolebanie $s(t)$ operezhaet po faze kolebanie $s_{1} (t)$ i otstaet po faze ot kolebaniya $s_{2} (t).$ Polnaya faza dlya kazhdogo iz treh kolebanii v proizvol'nyi moment vremeni otlichaetsya ot ih nachal'nyh faz na odnu i tu zhe velichinu $\omega _{0} t,$ kotoruyu pri postroenii vektornyh diagramm ne uchityvayut. Pri etom kolebanie izobrazhaetsya nepodvizhnym vektorom (ris. 1.6b), a chastota kolebaniya predpolagaetsya izvestnoi.

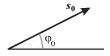Ris. 1.6b.

Slozhenie vzaimno-perpendikulyarnyh kolebanii.

Rassmotrim kolebatel'nuyu sistemu, sostoyashuyu iz tochechnogo gruza massy $m$ i chetyreh svyazannyh s nim pruzhin (ris. 1.7) - uslozhnennyi variant rassmotrennogo vyshe pruzhinnogo mayatnika.

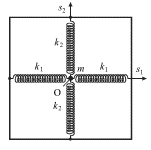Ris. 1.7.

Esli massa dvizhetsya po gladkoi gorizontal'noi poverhnosti (na risunke pokazan vid sverhu), to ee mgnovennoe raspolozhenie opisyvaetsya dvumya smesheniyami iz polozheniya ravnovesiya - tochki O: $s_{1} (t)$ i $s_{2} (t).$ Takaya sistema obladaet dvumya stepenyami svobody. Budem schitat' smesheniya malymi, chtoby, vo-pervyh, vypolnyalsya zakon Guka, a, vo-vtoryh, pri smeshenii vdol' napravleniya $s_{1}$ deformacii pruzhin s zhestkost'yu $k_{2}$ ne privodili k skol'ko-nibud' zametnomu vkladu v vozvrashayushuyu silu $F_{1} = - 2k_{1} s_{1} .$ Analogichno, pri smeshenii v perpendikulyarnom napravlenii $s_{2}$ vozvrashayushaya sila $F_{2} = - 2k_{2} s_{2} .$ Pri takih usloviyah kolebaniya v dvuh vzaimno perpendikulyarnyh napravleniyah proishodyat nezavisimo drug ot druga:

$s_{1} (t) = s_{01} \sin (\omega _{01} t + \varphi _{1} ), \quad s_{2} (t) = s_{02} \sin (\omega _{02} t + \varphi _{2} ).$

(1.19)

Zdes' sobstvennye chastoty garmonicheskih kolebanii ravny

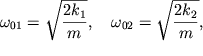$\omega _{01} = \sqrt {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle 2k_{1} }}{\displaystyle {\displaystyle m}}}}, \quad \omega _{02} = \sqrt {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle 2k_{2} }}{\displaystyle {\displaystyle m}}}},$

(1.20)

a amplitudy i nachal'nye fazy opredelyayutsya nachal'nymi usloviyami.

Pri vozbuzhdenii kolebanii v takoi sisteme pri proizvol'nom sootnoshenii sobstvennyh chastot $\omega _{01}$ i $\omega _{02}$ traektoriya koleblyushegosya gruza mozhet byt' chrezvychaino slozhnoi. Ee, v principe, mozhno proanalizirovat', prinimaya vo vnimanie tot fakt, chto rezul'tiruyushee dvizhenie gruza yavlyaetsya superpoziciei dvuh vzaimno-perpendikulyarnyh nezavisimyh kolebanii.

Rassmotrim vnachale dvizhenie gruza, esli $\omega _{01} = \omega _{02} = \omega _{0}$ (zhestkosti vseh pruzhin odinakovy). Chtoby poluchit' traektoriyu dvizheniya, isklyuchim iz (1.19) tekushee vremya. Dlya etogo perepishem (1.19) v vide:

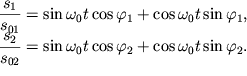$\begin{array}{ l} {\displaystyle \frac{\displaystyle {\displaystyle s_{1} }}{\displaystyle {\displaystyle s_{01} }}} = \sin \omega _{0} t\cos \varphi _{1} + \cos \omega _{0} t\sin \varphi _{1}, \\ {\displaystyle \frac{\displaystyle {\displaystyle s_{2} }}{\displaystyle {\displaystyle s_{02} }}} = \sin \omega _{0} t\cos \varphi _{2} + \cos \omega _{0} t\sin \varphi _{2} . \\ \end{array}$

(1.21)

Umnozhim pervoe uravnenie (1.21) na $\cos \varphi _{2},$ a vtoroe - na $\cos \varphi _{1}$ i vychtem vtoroe uravnenie iz pervogo. V rezul'tate poluchim

${\displaystyle \frac{\displaystyle {\displaystyle s_{1} }}{\displaystyle {\displaystyle s_{01} }}}\cos \varphi _{2} - {\displaystyle \frac{\displaystyle {\displaystyle s_{2} }}{\displaystyle {\displaystyle s_{02} }}}\cos \varphi _{1} = \cos \omega _{0} t\sin \left( {\displaystyle \varphi _{1} - \varphi _{2} } \right).$

(1.22a)

Teper' umnozhim pervoe uravnenie na $\sin \varphi _{2},$ a vtoroe - na $\sin \varphi _{1},$ povtorim vychitanie i poluchim

${\displaystyle \frac{\displaystyle {\displaystyle s_{1} }}{\displaystyle {\displaystyle s_{01} }}}\sin \varphi _{2} - {\displaystyle \frac{\displaystyle {\displaystyle s_{2} }}{\displaystyle {\displaystyle s_{02} }}}\sin \varphi _{1} = \sin \omega _{0} t\sin (\varphi _{2} - \varphi _{1} ).$

(1.22b)

Nakonec, vozvedem v kvadrat kazhdoe iz ravenstv (1.22) i slozhim ih. V rezul'tate vremya budet isklyucheno, a uravnenie traektorii dvizhushegosya gruza budet uravneniem ellipsa:

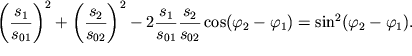$\left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle s_{1} }}{\displaystyle {\displaystyle s_{01} }}}} \right)^{2} + \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle s_{2} }}{\displaystyle {\displaystyle s_{02} }}}} \right)^{2} - 2{\displaystyle \frac{\displaystyle {\displaystyle s_{1} }}{\displaystyle {\displaystyle s_{01} }}}{\displaystyle \frac{\displaystyle {\displaystyle s_{2} }}{\displaystyle {\displaystyle s_{02} }}}\cos (\varphi _{2} - \varphi _{1} ) = \sin ^{2}(\varphi _{2} - \varphi _{1} ).$

(1.23)

Takim obrazom, v obshem sluchae gruz budet sovershat' periodicheskie dvizheniya po ellipticheskoi traektorii. Napravlenie dvizheniya vdol' traektorii i orientaciya ellipsa otnositel'no osei Os₁ i Os₂ zavisyat ot nachal'noi raznosti faz $\Delta \varphi = \varphi _{2} - \varphi _{1} .$ Na ris. 1.8 izobrazheny traektorii dvizheniya gruza pri razlichnyh znacheniyah $\Delta \varphi .$

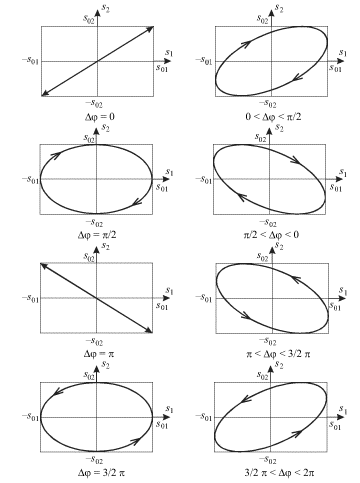Ris. 1.8.

Vse traektorii zaklyucheny v pryamougol'nik so storonami $2s_{01}$ i $2s_{02}.$ Pri $\Delta \varphi = 0$ i $\Delta \varphi = \pi$ gruz dvizhetsya po pryamoi linii. Pri $\Delta \varphi = \pi / 2$ i $\Delta \varphi = 3\pi / 2$ poluosi ellipsa sovpadayut s Os₁ i Os₂ (pri $s_{10} = s_{20}$ ellips vyrozhdaetsya v okruzhnost'). Pri raznosti faz $0 \lt \Delta \varphi \lt \pi$ gruz dvizhetsya po chasovoi strelke, a pri $\pi \lt \Delta \varphi \lt 2\pi$ - protiv chasovoi strelki.

Tipichnym primerom dvumernogo oscillyatora (mayatnika) yavlyaetsya elektron v atome, kotoryi dvizhetsya vokrug yadra po ellipticheskoi orbite s periodom obrasheniya $T\sim 10^{ - 15} s.$ Mozhno schitat', chto takoi elektron odnovremenno sovershaet dva vzaimno-perpendikulyarnyh kolebaniya s chastotoi $\omega _{0} = 2\pi / T\sim 10^{16}~s^{-1}.$

Esli chastoty dvuh vzaimno-perpendikulyarnyh kolebanii ne sovpadayut, no yavlyayutsya kratnymi: $m\omega _{02} = n\omega _{01},$ gde $m$ i $n$ - celye chisla, to traektorii dvizheniya predstavlyayut soboi zamknutye krivye, nazyvaemye figurami Lissazhu (ris. 1.9). Otmetim, chto otnoshenie chastot kolebanii ravno otnosheniyu chisel tochek kasaniya figury Lissazhu k storonam pryamougol'nika, v kotoryi ona vpisana.

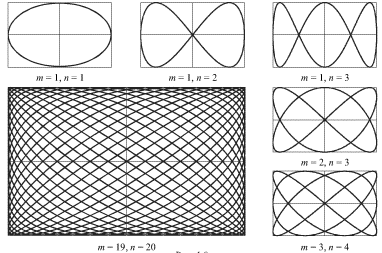Ris. 1.9.

Esli kratnost' mezhdu chastotami otsutstvuet, to traektorii ne yavlyayutsya zamknutymi i postepenno zapolnyayut ves' pryamougol'nik, napominaya nit' v klubke.

Nazad| Vpered

Publikacii s klyuchevymi slovami: kolebaniya - volny Publikacii so slovami: kolebaniya - volny
Sm. takzhe: Eho iz glubin krasnogo giganta

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

Kolebaniya i volny. Lekcii.

Metod vektornyh diagramm.

Slozhenie vzaimno-perpendikulyarnyh kolebanii.