Astronet > Kolebaniya i volny

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Kolebaniya i volny. Lekcii.

V.A.Aleshkevich, L.G.Dedenko, V.A.Karavaev (Fizicheskii fakul'tet MGU)
Izdatel'stvo Fizicheskogo fakul'teta MGU, 2001 g. Soderzhanie

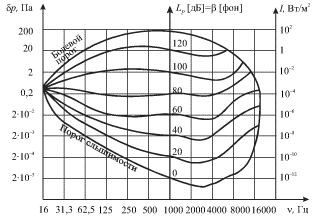
Na ris. 5.12 izobrazhena "diagramma sluha", na kotoroi pokazany oblasti chastot i zvukovyh davlenii, a takzhe urovni intensivnosti zvukov, vosprinimaemyh chelovecheskim uhom. Normal'noe uho slyshit tol'ko te zvuki, kotorye lezhat vnutri etoi oblasti. Nizhnyaya granica oblasti harakterizuet zavisimost' poroga slyshimosti ot chastoty, a verhnyaya - porog bolevogo oshusheniya, kogda volna perestaet vosprinimat'sya kak zvuk, vyzyvaya v uhe oshushenie boli i davleniya. Otmetim, chto chelovecheskoe uho yavlyaetsya unikal'nym priemnikom akusticheskih voln, vosprinimayushim zvuki, razlichayushiesya po intensivnosti na 12-15 poryadkov v oblasti chastot okolo 1 kGc, gde diagramma sluha imeet naibol'shee vertikal'noe sechenie. Iz diagrammy vidno, chto pri odinakovom zvukovom davlenii i odinakovoi intensivnosti zvuki razlichnoi chastoty mogut vosprinimat'sya, kak zvuki raznoi gromkosti $\beta.$ Poetomu v akustike, pomimo sub'ektivnoi velichiny - gromkosti zvuka $\beta,$ ocenivaemoi na sluh, ispol'zuyutsya i ob'ektivnye harakteristiki zvuka, kotorye mogut byt' neposredstvenno izmereny, - uroven' zvukovogo davleniya $L_{p}$ i ravnyi emu uroven' intensivnosti. Poskol'ku soglasno (5.17) intensivnost' proporcional'na kvadratu zvukovogo davleniya, obe eti harakteristiki opredelyayutsya formuloi:

$L_{p} = 2\lg {\displaystyle \frac{\displaystyle {\displaystyle \delta p}}{\displaystyle {\displaystyle \delta p_{por} }}} = \lg {\displaystyle \frac{\displaystyle {\displaystyle I}}{\displaystyle {\displaystyle I_{por} }}}.$

(5.30)

Ris. 5.12.

V principe, $L_{p}$ - velichina bezrazmernaya, no dlya chislennogo znacheniya logarifma ispol'zuyut nazvanie "Bel" (v chest' izobretatelya telefona G. Bella). Na praktike obychno ispol'zuyut v 10 raz men'shuyu edinicu - "decibel", tak chto (5.30) prinimaet vid:

$L_{p} [dB] = 20\lg {\displaystyle \frac{\displaystyle {\displaystyle \delta p}}{\displaystyle {\displaystyle \delta p_{por} }}} = 10\lg {\displaystyle \frac{\displaystyle {\displaystyle I}}{\displaystyle {\displaystyle I_{por} }}}.$

(5.30a)

V opredelenii $L_{p}$ prinyato ispol'zovat' standartnyi porog slyshimosti $\delta p_{por} = 2 \cdot 10^{ - 5} Pa,$ a sootvetstvuyushee emu znachenie minimal'noi intensivnosti $I_{por}$ zavisit, soglasno (5.17), ot sredy, v kotoroi rasprostranyaetsya zvuk, i dlya vozduha pri normal'nyh usloviyah sostavlyaet $I_{por} = 10^{ - 12} Vt/m^{2}.$

Dlya gromkosti zvuka $\beta$ ispol'zuyut edinicu pod nazvaniem "fon". Gromkost' tona v fonah dlya lyuboi chastoty ravna urovnyu zvukovogo davleniya v decibelah dlya tona s chastotoi $\nu = 1 kGc,$ vosprinimaemogo kak zvuk toi zhe gromkosti.

Na ris. 5.12 izobrazheny takzhe krivye dlya urovnei ravnoi gromkosti pri razlichnyh urovnyah zvukovogo davleniya i intensivnosti, iz kotoryh vidno, chto pri $\nu = 1 kGc\; \beta = L_{p},$ a dlya drugih slyshimyh uhom chastot $\beta$ i $L_{p}$ mogut zametno otlichat'sya.

Akusticheskie rezonatory.

V ryade sluchaev voznikaet neobhodimost' vydeleniya garmonicheskih sostavlyayushih iz slozhnyh zvukovyh kolebanii. S takoi zadachei prihoditsya stalkivat'sya pri upomyanutom vyshe spektral'nom analize slozhnyh zvukov, pri sozdanii uzkopolosnyh priemnikov zvuka, chuvstvitel'nyh k opredelennoi chastote, muzykal'nyh instrumentov i dr. Dlya takih celei ispol'zuetsya akusticheskii rezonator - ustroistvo, obladayushee odnoi ili mnozhestvom sobstvennyh chastot.

Tipichnym primerom akusticheskoi sistemy, reagiruyushei lish' na odnu chastotu, yavlyaetsya sosud sfericheskoi formy s otkrytoi gorlovinoi (ris. 5.13), kotoryi nazyvaetsya rezonatorom Gel'mgol'ca. V zadnei chasti rezonatora imeetsya eshe odno malen'koe otverstie v vide sopla, sluzhashee dlya obnaruzheniya kolebanii. Vozduh v gorlovine yavlyaetsya koleblyusheisya massoi. Pri smeshenii etoi massy, naprimer, v storonu sfericheskogo ob'ema $V$ vozduh v etom ob'eme slegka szhimaetsya, i voznikayushie sily izbytochnogo davleniya vypolnyayut rol' vozvrashayushei sily. Esli ploshad' gorloviny ravna $S,$ a ee dlina - $\ell,$ to massa koleblyushegosya stolba ravna $m = \rho _{0} \ell S,$ gde $\rho _{0}$ - plotnost' nevozmushennogo vozduha. Pri smeshenii massy $m$ na rasstoyanie $\xi \ll \ell$ (polozhitel'noe napravlenie osi $O\xi$ pokazano na risunke) plotnost' vozduha izmenyaetsya na velichinu $\delta \rho,$ udovletvoryayushuyu ravenstvu

${\displaystyle \frac{\displaystyle {\displaystyle \delta \rho }}{\displaystyle {\displaystyle \rho _{0} }}} = - {\displaystyle \frac{\displaystyle {\displaystyle S \cdot \xi }}{\displaystyle {\displaystyle V}}}.$

(5.31)

Soglasno (5.7), izbytochnoe davlenie okazyvaetsya ravnym

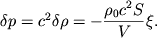$\delta p = c^{2}\delta \rho = - {\displaystyle \frac{\displaystyle {\displaystyle \rho _{0} c^{2}S}}{\displaystyle {\displaystyle V}}}\xi.$

(5.32)

Sledovatel'no, uravnenie dvizheniya stolba vozduha prinimaet vid

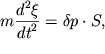$m{\displaystyle \frac{\displaystyle {\displaystyle d^{2}\xi }}{\displaystyle {\displaystyle dt^{2}}}} = \delta p \cdot S,$

ili

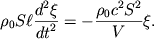$\rho _{0} S\ell {\displaystyle \frac{\displaystyle {\displaystyle d^{2}\xi }}{\displaystyle {\displaystyle dt^{2}}}} = - {\displaystyle \frac{\displaystyle {\displaystyle \rho _{0} c^{2}S^{2}}}{\displaystyle {\displaystyle V}}}\xi.$

(5.33)

Otsyuda nahodim, chto sobstvennaya chastota kolebanii stolba vozduha v gorlovine, ili chastota rezonatora Gel'mgol'ca, ravna

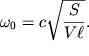$\omega _{0} = c\sqrt {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle S}}{\displaystyle {\displaystyle V\ell }}}}.$

(5.34)

Pri ob'eme rezonatora $V = 10^{ - 3} m^{3},$ ploshadi otverstiya gorloviny $S = 1 sm^{2}$ i ee dline $\ell = 1 sm,$ skorosti zvuka $c = 334 m/s$ dlya chastoty $\nu _{0}$ poluchim velichinu

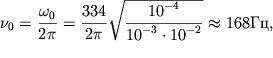$\nu _{0} = {\displaystyle \frac{\displaystyle {\displaystyle \omega _{0} }}{\displaystyle {\displaystyle 2\pi }}} = {\displaystyle \frac{\displaystyle {\displaystyle 334}}{\displaystyle {\displaystyle 2\pi }}}\sqrt {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle 10^{ - 4}}}{\displaystyle {\displaystyle 10^{ - 3} \cdot 10^{ - 2}}}}} \approx 168 Gc,$

(5.35)

sootvetstvuyushuyu slyshimomu diapazonu zvukovyh chastot.

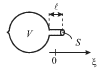Ris. 5.13.

Zavisimost' sobstvennoi chastoty kolebanii rezonatora ot ego parametrov i prezhde vsego ot ob'ema $V$ effektno demonstriruetsya v sleduyushem opyte (ris. 5.14). Pered dinamikom D, podklyuchennym k generatoru zvukovoi chastoty G ustanavlivayutsya neskol'ko rezonatorov, otlichayushihsya svoimi razmerami. Okolo zadnego otverstiya kazhdogo iz rezonatorov pomeshaetsya legkii bumazhnyi propeller-vertushka, kotoryi mozhet vrashat'sya vokrug vertikal'noi osi. Pri plavnom uvelichenii chastoty zvukovogo generatora budet vozrastat' chastota akusticheskoi volny, ispuskaemoi dinamikom v napravlenii rezonatorov i igrayushei rol' garmonicheskoi vynuzhdayushei sily. Pri posledovatel'nom sovpadenii chastoty etoi volny $\nu$ s sobstvennymi chastotami $\nu _{1}, \nu _{2}$ i $\nu _{3}$ rezonatorov davlenie vozduha v ih ob'emah budet kolebat'sya s maksimal'noi (rezonansnoi) amplitudoi. Iz zadnih otverstii rezonatorov budut bit' sil'nye strui vozduha, chto fiksiruetsya po nachalu vrasheniya vertushek snachala u bol'shogo, zatem u srednego i, nakonec, u samogo malen'kogo rezonatora, imeyushego samuyu vysokuyu sobstvennuyu chastotu $\nu _{3} .$

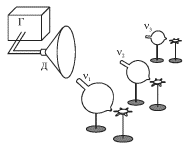Ris. 5.14.

Umestno otmetit', chto pri chastote rezonatora $\nu _{0} \sim 10^{2} Gc$ dlina vozbuzhdayushei ego volny $\lambda = c / \nu _{0} \approx 3,3 m.$ Eta dlina znachitel'no bol'she harakternyh razmerov rezonatora: $\lambda \gg V^{1 / 3}.$ Sledovatel'no, ne mozhet byt' i rechi o stoyachei akusticheskoi volne chastoty $\nu _{0}$ v samoi sfericheskoi polosti.

Odnako i v samoi polosti mozhno vozbudit' stoyachie volny s dlinoi $\lambda \le V^{1 / 3}$ i chastotoi $\nu = c / \lambda \ge c / V^{1 / 3}.$ Esli harakternyi razmer rezonatora $V^{1 / 3}\sim 10 sm,$ to chastoty etih voln $\nu \gt 3000 Gc.$ Takoi rezonator budet obladat' mnozhestvom sobstvennyh chastot v kilogercovom diapazone.

Naibolee prostym v izgotovlenii akusticheskim rezonatorom yavlyaetsya derevyannyi yashik ili truba, otkrytye libo s odnoi, libo s dvuh protivopolozhnyh storon.

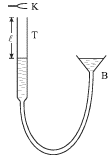
Prodelaem sleduyushii opyt. Zapolnim vodoi nizhnyuyu chast' vertikal'noi trubki T, ispol'zuya sistemu soobshayushihsya sosudov, i podnesem k verhnemu koncu zvuchashii na chastote $\nu$ kamerton K (ris. 5.15). Peremeshaya voronku V vverh, mozhno dobit'sya usileniya tonal'nogo zvuka, sozdavaemogo sistemoi "kamerton + chast' truby, zapolnennaya vozduhom". Eto usilenie budet pri sovpadenii chastoty $\nu$ s odnoi iz sobstvennyh chastot $\nu _{p}$ rezonatora - truby s vozduhom dlinoi $\ell,$ "zakrytoi" u nizhnego konca. Sobstvennye chastoty stoyachih voln v takom rezonatore legko podschitat', esli uchest', chto na nizhnem konce dolzhen byt' uzel smeshenii, a na verhnem - puchnost'. Eto vozmozhno lish' dlya dlin voln $\lambda _{p},$ udovletvoryayushih izlozhennomu v predydushei lekcii usloviyu (4.40):

$\ell = (2p - 1){\displaystyle \frac{\displaystyle {\displaystyle \lambda _{p} }}{\displaystyle {\displaystyle 4}}}, p = I, II, III, \ldots ,$

kogda na dline truby ukladyvaetsya nechetnoe chislo chetvertei dlin voln. Sootvetstvenno, chastoty kolebanii budut ravny

$\nu _{p} = {\displaystyle \frac{\displaystyle {\displaystyle c}}{\displaystyle {\displaystyle \lambda _{p} }}} = {\displaystyle \frac{\displaystyle {\displaystyle c}}{\displaystyle {\displaystyle 4\ell }}}(2p - 1).$

(5.36)

Hotya usilenie zvuka budet pri neskol'kih dlinah vozdushnogo stolba $\ell,$ odnako samym effektivnym ono budet pri $\nu = \nu _{I}$ ili $\ell = {\displaystyle \frac{\displaystyle {\displaystyle c}}{\displaystyle {\displaystyle 4\nu }}}.$

Ris. 5.15.

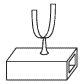
Osobo podcherknem, chto rezonator sozdaet bolee blagopriyatnye usloviya dlya zvuchaniya kamertona, pozvolyaya pereraspredelit', a stalo byt' i usilit' zvuk po opredelennym napravleniyam. Imenno poetomu v opytah kamertony ustanavlivayut na derevyannyi yashik, otkrytyi s odnogo konca i nastroennyi na chastotu kamertona (ris. 5.16).

Ris. 5-16.

Nazad| Vpered

Publikacii s klyuchevymi slovami: kolebaniya - volny Publikacii so slovami: kolebaniya - volny
Sm. takzhe: Eho iz glubin krasnogo giganta

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce