Astronet > Kolebaniya i volny

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Kolebaniya i volny. Lekcii.

V.A.Aleshkevich, L.G.Dedenko, V.A.Karavaev (Fizicheskii fakul'tet MGU)
Izdatel'stvo Fizicheskogo fakul'teta MGU, 2001 g. Soderzhanie

Nekotorye svedeniya o muzykal'nyh instrumentah.

Derevyannye deki muzykal'nyh instrumentov vypolnyayut funkcii rezonatorov, obespechivaya horoshie usloviya zvuchaniya. Chastoty strunnyh instrumentov ne zavisyat ot rezonatora. Osnovnaya chastota zvuka $\nu _{1}$ i chastoty obertonov zavisyat tol'ko ot massy, natyazheniya i dliny struny. Odnako tembr zvuka zavisit ot sposoba vozbuzhdeniya i ot reakcii rezonatora i effektivnosti, s kotoroi rezonator "podderzhivaet" eti chastoty i posylaet sootvetstvuyushie volny v okruzhayushee prostranstvo.

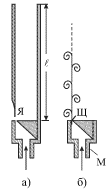
V duhovyh instrumentah formirovanie zvuka svyazano s nalichiem avtokolebanii i zavisit kak ot konstrukcii instrumenta, tak i ot sposoba, s pomosh'yu kotorogo vozduh vduvaetsya v instrument. V kachestve illyustracii rassmotrim kachestvenno process vozniknoveniya avtokolebanii v organnoi trube, razrez kotoroi izobrazhen na ris. 5.17a.

Ris. 5.17.

Pri ravnomernom postuplenii v mundshtuk M (situaciya b) vozduh prohodit cherez uzkuyu shel' Sh, za kotoroi obrazuetsya turbulentnyi potok. Obrazuyushayasya pri takom techenii vihrevaya dorozhka yavlyaetsya istochnikom "shelevogo" tona, osnovnaya chastota kotorogo obratno proporcional'na periodu sledovaniya vihrei $T_{v}.$ Po sushestvu sistema "mundshtuk + shel'" predstavlyaet soboi slozhnuyu avtokolebatel'nuyu sistemu, teoreticheskoe opisanie kotoroi - ser'eznaya problema.

Vihri, vyhodyashie iz sheli, poocheredno prohodyat sleva i sprava ot yazychka Ya, vyzyvaya ego vibraciyu (situaciya a). Yazychok okazyvaet periodicheskoe vozdeistvie na stolb vozduha v trube. Voznikayushie v stolbe impul'sy szhatiya, dobezhav do otkrytogo konca truby, otrazhayutsya v vide impul'sov razrezheniya i vozvrashayutsya k sheli cherez vremya $T = 2\ell / c$ ( $\ell$ - dlina truby, $c$ - skorost' zvuka v vozduhe), upravlyaya postupleniem vozduha cherez shel'. Takim obrazom, osnovnaya chastota $\nu _{1} = 1 / T$ formiruetsya rezonatornoi sistemoi. Odnako mozhno vduvat' vozduh tak, chtoby v trube odnovremenno sushestvovali dva impul'sa szhatiya, i my uslyshim zvuchanie truby na chastote pervogo obertona (udvoennoi chastote).

Organnye truby obychno konstruiruyutsya dlya zvuchaniya na osnovnoi chastote. V duhovyh instrumentah vozbuzhdayushim vibratorom (analogom yazychka Ya v organnoi trube) mozhno upravlyat', chtoby posylat' v trubu odin ili bolee impul'sov, prezhde chem pervyi otrazitsya ot otkrytogo konca. Vysota zvuka instrumenta opredelyaetsya kolichestvom impul'sov v sekundu, otrazhennyh ot otkrytogo konca duhovogo instrumenta.

Proiznosimye chelovekom zvuki svyazany s tem, chto golosovye svyazki gortani vibriruyut pod naporom dvizhushegosya vozduha, a gortan' yavlyaetsya ob'emnym rezonatorom. Kak pravilo, u muzhchin ob'em gortani bol'she, chem u zhenshin, poetomu v sootvetstvii s formuloi (5.34) muzhskie golosa bolee nizkie.

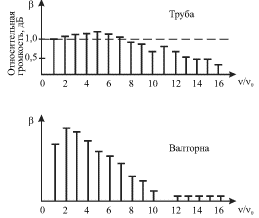
Na ris. 5.18 pokazany spektry zvukov, izvlekaemyh na trube i valtorne s odinakovoi osnovnoi chastotoi $\nu _{0} = 440 Gc.$ Po osi ordinat otlozhena gromkost' $\beta$ (normirovana na gromkost' volny osnovnoi chastoty). V spektre zvuka valtorny otsutstvuyut chastoty $\nu \gt 10 kGc,$ poetomu ee zvuk bolee priglushennyi, nezheli zvuk truby.

Ris. 5.18.

Zavershaya opisanie osnovnyh principov deistviya istochnikov zvuka i muzykal'nyh instrumentov, umestno upomyanut' o dvuh akusticheskih effektah, s proyavleniyami kotoryh my prakticheski ezhednevno vstrechaemsya.

Effekt Doplera.

Nablyudaya za prohodyashim mimo poezdom ili dvizhushimsya avtomobilem, my zamechaem, chto vysota tona podavaemogo imi zvukovogo signala postoyanno izmenyaetsya. Eto i est' odno iz proyavlenii effekta Doplera, sostoyashego v izmenenii chastoty zvuka pri otnositel'nom dvizhenii istochnika i priemnika. Rassmotrim eto yavlenie neskol'ko podrobnee.

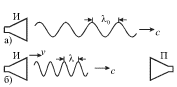
Pust' istochnik I (ris. 5.19a) izluchaet monohromaticheskuyu (t.e. garmonicheskuyu) akusticheskuyu volnu chastoty $\nu _{0}.$ Togda dlina etoi volny, rasprostranyayusheisya v vozduhe so skorost'yu s, budet ravna:

$\lambda _{0} = c / \nu _{0}.$

(5.37)

Ris. 5.19.

Esli teper' istochnik budet dvigat'sya so skorost'yu $v \lt c$ v napravlenii rasprostraneniya volny, to volna budet "otryvat'sya" ot istochnika so skorost'yu $c - v,$ i ee dlina umen'shitsya (ris. 5.19b):

$\lambda = {\displaystyle \frac{\displaystyle {\displaystyle c - v}}{\displaystyle {\displaystyle \nu _{0} }}}.$

(5.38)

Dostignuv nepodvizhnogo priemnika P, eta volna budet vozdeistvovat' na nego s chastotoi

$\nu = {\displaystyle \frac{\displaystyle {\displaystyle c}}{\displaystyle {\displaystyle \lambda }}} = \nu _{0} {\displaystyle \frac{\displaystyle {\displaystyle c}}{\displaystyle {\displaystyle c - v}}} = \nu _{0} {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 1 - v / c}}},$

(5.39)

kotoraya budet bol'she ishodnoi chastoty $\nu _{0}.$ Pri dvizhenii istochnika v protivopolozhnom napravlenii eta chastota umen'shitsya. Imenno eto izmenenie chastoty tona signala my fiksiruem pri priblizhenii i posleduyushem udalenii poezda ili avtomobilya.

Izmenenie chastoty budet takzhe i pri dvizhenii priemnika P, odnako fizicheskaya prichina etogo izmeneniya sostoit v tom, chto volna s dlinoi $\lambda _{0} = c / \nu _{0}$ budet postupat' v priemnik so skorost'yu $v + c$ (esli priemnik dvizhetsya navstrechu volne). Sledovatel'no, chastota vozdeistviya na priemnik budet ravna

$\nu = {\displaystyle \frac{\displaystyle {\displaystyle c + v}}{\displaystyle {\displaystyle \lambda _{0} }}} = \nu _{0} {\displaystyle \frac{\displaystyle {\displaystyle c + v}}{\displaystyle {\displaystyle c}}} = \nu _{0} \left( {\displaystyle 1 + {\displaystyle \frac{\displaystyle {\displaystyle v}}{\displaystyle {\displaystyle c}}}} \right)$

(5.40)

i prevysit ishodnuyu chastotu.

V silu razlichiya fizicheskih prichin, privodyashih k izmeneniyu chastoty pri dvizhenii istochnika i priemnika, raznyatsya i formuly (5.39) i (5.40). Odnako pri $v \ll c,$ kak netrudno ubedit'sya, s tochnost'yu do chlenov poryadka $\left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle v}}{\displaystyle {\displaystyle c}}}} \right)^{2}$ formula (5.39) mozhet byt' zapisana v vide (5.40).

Pri odnovremennom dvizhenii navstrechu drug drugu istochnika so skorost'yu $v_{i}$ i priemnika so skorost'yu $v_{p}$ obe formuly mozhno ob'edinit' v odnu

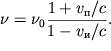$\nu = \nu _{0} {\displaystyle \frac{\displaystyle {\displaystyle 1 + v_{p} / c}}{\displaystyle {\displaystyle 1 - v_{i} / c}}}.$

(5.41)

Pri udalenii istochnika ili priemnika v formule (5.41) sleduet izmenit' znak pri sootvetstvuyushei skorosti.

Pri skorostyah $v \gt c$ formiruyutsya udarnye volny, i formuly, opisyvayushie izmenenie chastoty, stanovyatsya nespravedlivymi.

Binaural'nyi effekt.

Etot effekt predstavlyaet soboi psihofiziologicheskoe yavlenie, zaklyuchayusheesya v slitnom vospriyatii zvukov, prinimaemyh pravym i levym uhom. On daet vozmozhnost' opredelit' napravlenie na istochnik zvuka i igraet sushestvennuyu rol' v muzykal'noi akustike (stereofoniya).

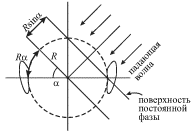
Risunok 5.20 illyustriruet etot effekt. Esli volna padaet pod uglom $\alpha$ k linii, soedinyayushei oba uha (punktirom izobrazhen kontur radiusa $R,$ imitiruyushii golovu cheloveka), to volna dostignet levogo uha pozdnee pravogo, a vremya zaderzhki sostavit velichinu

$\Delta t = {\displaystyle \frac{\displaystyle {\displaystyle R\sin \alpha + R\alpha }}{\displaystyle {\displaystyle c}}},$

(5.42)

gde $R\alpha$ - krivolineinyi put', prohodimyi zvukovoi volnoi pri ogibanii eyu golovy cheloveka za schet difrakcii (sm. nizhe).

Ris. 5.20.

Krome togo, poskol'ku golova chastichno ekraniruet zvuk, to amplituda volny, dostigayushei levogo uha, neskol'ko umen'shaetsya. Sovmestnoe deistvie etih dvuh faktorov daet cheloveku vozmozhnost' opredelit' napravlenie na istochnik zvuka. Esli period kolebanii zvukovoi volny sravnim so vremenem zaderzhki:

$\Delta t \le T / 2,$

(5.43)

to volny, padayushie pod uglom, vyzyvayut kolebaniya barabannyh pereponok levogo i pravogo uha so sdvigom faz $0 \le \Delta \varphi \le \pi,$ po kotoromu chelovek i opredelyaet napravlenie prihoda volny.

Esli polozhit' $R = 10 sm,\; \sin \alpha \approx 1,$ to dlya voln s periodom $T \lt 10^{ - 3} s\; (\nu \ge 1 kGc)$ uslovie (5.43) ne vypolnyaetsya, i opredelit' napravlenie po sdvigu fazy stanovitsya zatrudnitel'no. Odnako ostaetsya vozmozhnost' sravnit' amplitudy voln, dostigayushih oboih ushei, i tem samym opredelit' ugol $\alpha.$

Interferenciya voln.

V predydushei lekcii my poluchili uravnenie stoyachei volny (4.34), opisyvayushee kolebaniya shnura (ili inoi sredy), po kotoromu navstrechu drug drugu rasprostranyayutsya dve garmonicheskie volny odinakovoi chastoty $\omega$ i amplitudy $s_{0}.$ V rezul'tate nalozheniya voln proishodit pereraspredelenie v prostranstve ob'emnoi plotnosti energii kolebanii. V uzlah, gde volny vstrechayutsya v protivofaze, eta energiya ravna nulyu. V puchnostyah, naprotiv, volny skladyvayutsya v faze, i energiya maksimal'na. Yavlenie nalozheniya voln, privodyashee k pereraspredeleniyu v prostranstve ob'emnoi plotnosti energii kolebanii, nosit nazvanie interferencii.

Interferenciya yavlyaetsya odnim iz fundamental'nyh yavlenii, prisushih volnam razlichnoi prirody (akusticheskim, elektromagnitnym, volnam na poverhnosti zhidkosti, plazmennym volnam i dr.). Ona byla horosho izvestna eshe vo vremena N'yutona, kotoryi osushestvil zamechatel'nyi opyt, privedshii k otkrytiyu zakonomernostei interferencionnoi kartiny i poluchivshii nazvanie "kol'ca N'yutona". Eti zakonomernosti legko proslezhivayutsya v opytah po interferencii kapillyarnyh voln na poverhnosti zhidkosti. V sleduyushei lekcii daetsya opisanie haraktera dvizheniya chastic zhidkosti v takih volnah i ustanavlivaetsya svyaz' mezhdu chastotoi, dlinoi volny i skorost'yu ee rasprostraneniya.

Nazad| Vpered

Publikacii s klyuchevymi slovami: kolebaniya - volny Publikacii so slovami: kolebaniya - volny
Sm. takzhe: Eho iz glubin krasnogo giganta

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce