Astronet > Kolebaniya i volny

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Kolebaniya i volny. Lekcii.

V.A.Aleshkevich, L.G.Dedenko, V.A.Karavaev (Fizicheskii fakul'tet MGU)
Izdatel'stvo Fizicheskogo fakul'teta MGU, 2001 g. Soderzhanie

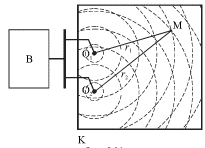
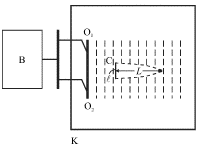
Odin iz takih opytov vyglyadit sleduyushim obrazom (ris. 5.21). V neglubokuyu kyuvetu K s bol'shoi ploshad'yu osnovaniya nalivayut vodu. Volny na ee poverhnosti vozbuzhdayut s pomosh'yu vibratora V, privodyashego v periodicheskoe dvizhenie dva malen'kih sharika O₁ i O₂, kotorye yavlyayutsya tochechnymi istochnikami voln. Eti shariki slegka pogruzheny v vodu i sovershayut sinhronnye kolebaniya s chastotoi $\nu \sim 10^{2} Gc$ v napravlenii, perpendikulyarnom poverhnosti vody. Ot kazhdogo iz tochechnyh istochnikov rasprostranyaetsya volna s dlinoi $\lambda \sim 3 mm$ i skorost'yu $c\sim 40 sm/s.$ Grebni etih voln v fiksirovannyi moment vremeni izobrazheny na risunke punktirom. V rezul'tate nalozheniya voln obrazuetsya interferencionnaya kartina, kotoruyu udobno nablyudat' v stroboskopicheskom osveshenii (osveshaya ee vspyshkami sveta, sleduyushimi takzhe s chastotoi $\nu \sim 10^{2} Gc$ ). Pri takom osveshenii volny budut kazat'sya prakticheski nepodvizhnymi.

Ris. 5.21.

Naibolee sil'nye vozmusheniya poverhnosti budut nablyudat'sya v teh mestah, gde volny skladyvayutsya v faze. Govoryat, chto zdes' raspolagayutsya interferencionnye maksimumy. V mestah, kuda volny prihodyat v protivofaze, poverhnost' budet prakticheski ne vozmushena: zdes' raspolagayutsya interferencionnye minimumy. Vozmushenie poverhnosti v proizvol'noi tochke M zavisit ot raznosti hoda $\Delta r = r_{2} - r_{1},$ gde $r_{1}$ i $r_{2}$ - rasstoyaniya ot tochki M do sootvetstvuyushego tochechnogo istochnika. Deistvitel'no, smeshenie s poverhnosti zhidkosti v tochke M mozhno rassmatrivat' kak rezul'tat nalozheniya dvuh sinusoidal'nyh (t.e. monohromaticheskih) voln, proshedshih rasstoyaniya $r_{1}$ i $r_{2}$ :

$s(t) = s_{0} \sin (\omega t - kr_{1} - \varphi _{1} ) + s_{0} \sin (\omega t - kr_{2} - \varphi _{2} ).$

(5.44)

Zdes' predpolagaetsya, chto obe volny v tochke M imeyut odinakovye amplitudy (hotya eto i ne sovsem verno), i postoyannye fazovye dobavki $\varphi _{1}$ i $\varphi _{2},$ tak chto ih raznost' $\Delta \varphi = \varphi _{2} - \varphi _{1}$ ne zavisit ot vremeni.

Vypolnyaya v (5.44) summirovanie, poluchaem:

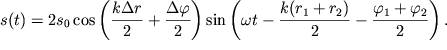$s(t) = 2s_{0} \cos \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle k\Delta r}}{\displaystyle {\displaystyle 2}}} + {\displaystyle \frac{\displaystyle {\displaystyle \Delta \varphi }}{\displaystyle {\displaystyle 2}}}} \right)\sin \left( {\displaystyle \omega t - {\displaystyle \frac{\displaystyle {\displaystyle k(r_{1} + r_{2} )}}{\displaystyle {\displaystyle 2}}} - {\displaystyle \frac{\displaystyle {\displaystyle \varphi _{1} + \varphi _{2} }}{\displaystyle {\displaystyle 2}}}} \right).$

(5.45)

Esli polozhit' dlya prostoty $\Delta \varphi = 0,$ to polozhenie interferencionnyh maksimumov opredelyaetsya iz usloviya

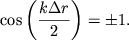$\cos \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle k\Delta r}}{\displaystyle {\displaystyle 2}}}} \right) = \pm 1.$

(5.46)

Poskol'ku $k = 2\pi / \lambda,$ to poslednemu usloviyu sootvetstvuet raznost' hoda

$\Delta r = r_{2} - r_{1} = m\lambda,$

(5.47)

gde $m = 0, \pm 1, \pm 2, \ldots.$

Kazhdomu maksimumu prinyato prisvaivat' poryadkovyi nomer, opredelyaemyi sootvetstvuyushim chislom $m$ (maksimum nulevogo, pervogo, minus pervogo i t.d. poryadka). Interferencionnye minimumy raspolagayutsya v teh mestah, gde

$\Delta r = r_{2} - r_{1} = (2m + 1){\displaystyle \frac{\displaystyle {\displaystyle \lambda }}{\displaystyle {\displaystyle 2}}},$

(5.48)

i tak zhe numeruyutsya $(m = 0, \pm 1, \pm 2, \ldots).$

Rassmotrennaya interferencionnaya kartina sootvetstvuet idealizirovannoi situacii. Real'nye volny dazhe v luchshem sluchae yavlyayutsya kvazimonohromaticheskimi. Dlya takih voln amplitudy $s_{0}$ i fazy $\varphi _{1}$ i $\varphi _{2}$ yavlyayutsya medlenno menyayushimisya funkciyami vremeni (zametnye izmeneniya etih funkcii proishodyat za vremya $\tau \gg T = {\displaystyle \frac{\displaystyle {\displaystyle 2\pi }}{\displaystyle {\displaystyle \omega }}}$ ). Odnako, esli oba sharika privodyatsya v kolebatel'noe dvizhenie odnim vibratorom, raznost' faz $\Delta \varphi$ v (5.45) ostaetsya postoyannoi, polozhenie interferencionnyh maksimumov zadaetsya formuloi (5.47) i ne zavisit ot vremeni.

V prakticheski vazhnyh sluchayah istochniki interferiruyushih voln mogut byt' nezavisimy. V nashem opyte eto mozhno osushestvit', esli ispol'zovat' dva vibratora, k kazhdomu iz kotoryh prisoedinen malen'kii sharik. Togda raznost' faz $\Delta \varphi$ budet takzhe izmenyat'sya na masshtabe vremeni $\tau,$ i ee mozhno zapisat' v vide

$\Delta \varphi (t) = \overline {\displaystyle \Delta \varphi } + \delta (t),$

(5.49)

gde $\overline {\displaystyle \Delta \varphi }$ - srednee po vremeni znachenie raznosti faz, $\delta (t)$ - znakoperemennaya funkciya. Schitaya dlya prostoty v (5.45) $s_{0} = {\displaystyle \rm const},$ prihodim k vyvodu, chto interferencionnaya kartina, kak celoe, budet dostatochno haotichno smeshat'sya v raznye storony. Esli takuyu kartinu snimat' na kinoplenku so vremenem ekspozicii kadra $\Delta t \gt \tau ,$ to na kazhdom kadre budet otpechatana usrednennaya za vremya $\Delta t$ "razmazannaya" kartina. Ona mozhet stat' sovsem nerazlichimoi, esli interferencionnye maksimumy budut smeshat'sya na velichiny, ravnye ili prevyshayushie rasstoyaniya mezhdu sosednimi maksimumami. Takaya situaciya dostatochno chasto vstrechaetsya pri interferencii svetovyh voln. Chtoby polnogo "smazyvaniya" kartiny ne proizoshlo, ochevidno, neobhodimo vypolnenie sleduyushego usloviya:

$|\delta (t)| \ll 2\pi.$

(5.50)

Chem luchshe vypolnyaetsya eto neravenstvo, tem vyshe kachestvo kartiny. Tak, naprimer, dlya svetovyh voln $\tau \sim 10^{ - 9}\div 10^{ - 12} s,$ i pri vizual'nom nablyudenii (dlya organov zreniya $\Delta t\sim 0,1 s$ ) my vsegda registriruem "razmazannuyu" interferencionnuyu kartinu.

S kachestvom kartiny napryamuyu svyazano ponyatie kogerentnosti interferiruyushih voln. Kogerentnost' harakterizuetsya bezrazmernym koefficientom $\gamma$ (stepen'yu kogerentnosti), kotoryi mozhet menyat'sya v intervale $0 \lt \gamma \lt 1.$ Chem vyshe kachestvo kartiny, tem bol'she stepen' kogerentnosti. Dlya monohromaticheskih voln, konechno, $\gamma = 1.$

Etim zamechaniem o kogerentnosti voln my zdes' i ogranichimsya, a detal'noe opisanie etogo ponyatiya budet dano v kurse "Optika".

Difrakciya voln.

V uproshennom smysle pod difrakciei ponimayut krug yavlenii, v kotoryh proyavlyaetsya otstuplenie ot pryamolineinogo rasprostraneniya voln. Takoe ponimanie difrakcii, voobshe govorya, neverno, poskol'ku pryamolineinoe rasprostranenie voln yavlyaetsya lish' opredelennym priblizheniem. Deistvitel'no, specifika lyubogo volnovogo dvizheniya proyavlyaetsya v tom, chto eto dvizhenie, vozniknuv vnachale v ogranichennoi oblasti, stremitsya rasprostranit'sya v ravnoi stepeni vo vse storony. Vyborom special'noi formy etoi oblasti mozhno dobit'sya togo, chto volna pobezhit preimushestvenno v nekotoryh napravleniyah. Vdol' odnogo iz takih napravlenii pobezhit fragment volny, kotoryi s opredelennoi tochnost'yu mozhno schitat' dvizhushimsya pryamolineino.

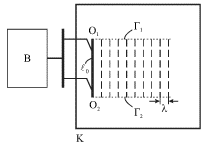
Dlya nablyudeniya osnovnyh zakonomernostei difrakcii vidoizmenim harakter vozbuzhdeniya voln na poverhnosti vody v opisannom ranee opyte. V kachestve istochnika volny vmesto sharikov budem ispol'zovat' plastinu O₁O₂, dlina kotoroi $\ell _{0} = (3\div 5) sm,$ t.e. zametno prevyshaet dlinu volny $\lambda \sim 3 mm$ (ris. 5.22). V rezul'tate po poverhnosti vody pobezhit "ploskaya" volna v napravlenii, perpendikulyarnom plastine. Otchetlivo nablyudayutsya dve pryamolineinye granicy G₁ i G₂, otdelyayushie vozmushennuyu volnoi i gladkuyu chasti poverhnosti vody. Dlya etoi poslednei chasti mozhno upotrebit' zaimstvovannyi iz optiki termin: "oblast' geometricheskoi teni". Samu volnu chasto nazyvayut volnovym puchkom, ili luchom. V etom eksperimente mozhno schitat', chto volna rasprostranyaetsya pryamolineino i ne zahodit v oblast' teni. Eto svyazano s tem, chto razmer ee volnovogo fronta $\ell _{0} \gg \lambda.$

Ris. 5.22.

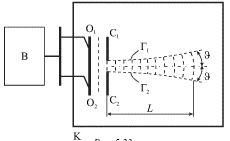
Umen'shim teper' etot razmer. Eto naibolee prosto osushestvit', esli parallel'no plastine O₁O₂ ustanovit' dve vertikal'nye stenki S₁ i S₂, rasstoyanie $\ell$ mezhdu kotorymi mozhno izmenyat' (ris. 5.23).

Ris. 5.23.

Esli sdelat' $\ell \leq 5\lambda \approx 15 mm,$ to volna nachnet postepenno zahodit' v oblast' teni, a ee front budet iskrivlyat'sya. Na nekotorom harakternom rasstoyanii $L$ volnovoi puchok priobretet zametnuyu uglovuyu rashodimost' i dalee budet rasprostranyat'sya po chasti poverhnosti, ogranichennoi uglom $2\vartheta.$ Pri umen'shenii zazora $\ell$ mezhdu stenkami ugol $2\vartheta$ vozrastaet, a rasstoyanie $L$ umen'shaetsya. Eto otstuplenie ot pryamolineinogo rasprostraneniya yavlyaetsya rezul'tatom difrakcii, sushestvenno togda, kogda $\ell \sim \lambda.$

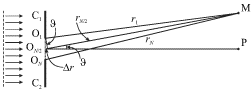
Ne sostavlyaet truda ocenit' velichiny $\vartheta$ i $L,$ ispol'zuya podhod, predlozhennyi francuzskim uchenym O. Frenelem v XIX stoletii dlya ob'yasneniya difrakcii svetovyh voln. Sleduya Frenelyu, uchastok fronta padayushei volny v zazore mezhdu stenkami mozhno rassmatrivat' kak cepochku iz $N \gg 1$ blizko raspolozhennyh odinakovyh tochechnyh istochnikov $O_{1}, O_{2}, \ldots, O_{N}$ (ris. 5.24).

Ris. 5.24.

Vozmushenie v lyuboi tochke M poverhnosti vody est' rezul'tat interferencii $N$ voln ot etih, tak nazyvaemyh "vtorichnyh" istochnikov, i zavisit ot raznosti hoda vseh interferiruyushih voln. V prakticheski vazhnyh sluchayah rasstoyaniya $r_{1}, r_{2}, \ldots, r_{N} \gg \ell,$ poetomu otrezki $O_{1}M, O_{2}M, \ldots, O_{N}M$ mozhno schitat' parallel'nymi. Ponyatno, chto v tochku P, lezhashuyu na osi volnovogo puchka, interferiruyushie volny prihodyat v faze i vozmushenie poverhnosti v nei budet maksimal'nym. Naprotiv, v tochke M volny mogut pogasit' drug druga, esli raznost' hoda $\Delta r = r_{N / 2} - r_{1}$ mezhdu volnami ot krainego istochnika O₁ i srednego istochnika $O_{N / 2}$ budet ravna $\lambda / 2.$ Poskol'ku eta raznost', kak vidno iz ris. 5.24, ravna ${\displaystyle \frac{\displaystyle {\displaystyle \ell }}{\displaystyle {\displaystyle 2}}}\sin \vartheta,$ to

$\Delta r = {\displaystyle \frac{\displaystyle {\displaystyle \ell }}{\displaystyle {\displaystyle 2}}}\sin \vartheta = {\displaystyle \frac{\displaystyle {\displaystyle \lambda }}{\displaystyle {\displaystyle 2}}}.$

(5.51)

Analogichno, v protivofaze budut prihodit' volny i ot drugih par istochnikov $(O_{2}, O_{N / 2 + 1};\; O_{3}, O_{N / 2 + 2};\; \ldots;\; O_{N / 2 - 1}, O_{N}).$ Govoryat, chto v tochke M budet nablyudat'sya pervyi minimum difrakcionnoi kartiny. Ne sostavlyaet truda napisat' uslovie, podobnoe (5.51), i dlya drugih minimumov. Odnako, kak pokazyvaet strogii analiz, bolee 90% vsei energii perenositsya volnoi v predelah ugla $2\vartheta.$ Poetomu na risunke (5.23) granicy G₁ i G₂ ves'ma uslovny i ocherchivayut lish' osnovnuyu, naibolee energoemkuyu chast' puchka.

Dlya ocenki difrakcionnoi rashodimosti volnovyh puchkov ispol'zuetsya ugol $\vartheta,$ kotoryi pri $\ell \gg \lambda$ ocenivaetsya soglasno (5.51) po formule

$\vartheta \approx {\displaystyle \frac{\displaystyle {\displaystyle \lambda }}{\displaystyle {l}}}.$

(5.52)

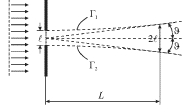
Takuyu rashodimost' puchok priobretaet na nekotorom harakternom rasstoyanii $L.$ Ego mozhno legko ocenit' iz risunka 5.25, na kotorom punktirom izobrazheny asimptoty k granicam G₁ i G₂. Budem uslovno schitat', chto na rasstoyanii $L$ poperechnyi razmer puchka udvoilsya i stal ravnym $2\ell.$ Togda s uchetom (5.52) my mozhem zapisat':

$\vartheta = {\displaystyle \frac{\displaystyle {\displaystyle \ell }}{\displaystyle {l}}} = {\displaystyle \frac{\displaystyle {\displaystyle \lambda }}{\displaystyle {\displaystyle \ell }}}.$

(5.53)

Otsyuda

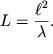$L = {\displaystyle \frac{\displaystyle {\displaystyle \ell ^{2}}}{\displaystyle {\displaystyle \lambda }}}.$

(5.54)

Velichina $L$ nazyvaetsya difrakcionnoi dlinoi puchka s dlinoi volny $\lambda$ i poperechnym razmerom $\ell.$ Ona opredelyaet masshtab rasstoyanii, na kotoryh razvivaetsya zametnaya difrakciya puchka.

Ris. 5.25.

Sdelaem nekotorye ocenki. V opyte, izobrazhennom na risunke (5.22), $\ell = 5 sm,\; \lambda = 3 mm,$ i $L\sim 80 sm.$ Eto oznachaet, chto v kyuvete difrakciya prosto ne uspevaet zametno razvit'sya. Pri umen'shenii $\ell$ (ris. 5.23) do velichiny $\ell = 5\lambda = 15 mm,$ difrakcionnaya dlina puchka $L = 7,5 sm,$ i difrakciya stanovitsya otchetlivo vidna.

Esli na puti volnovogo puchka postavit' prepyatstvie - stenku S (ris. 5.26), to srazu za stenkoi budet ten', odnako volna, proidya rasstoyanie $\sim L = \ell ^{2} / \lambda,$ obognet prepyatstvie. Illyustraciei k skazannomu yavlyaetsya, naprimer, vozmozhnost' uslyshat' zvukovoi signal avtomobilya, nahodyas' pozadi nebol'shogo stroeniya. Odnako za mnogoetazhnyi dom zvuk prakticheski ne pronikaet.

Ris. 5.26.

Nazad| Vpered

Publikacii s klyuchevymi slovami: kolebaniya - volny Publikacii so slovami: kolebaniya - volny
Sm. takzhe: Eho iz glubin krasnogo giganta

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce