Astronet > Kolebaniya i volny

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Kolebaniya i volny. Lekcii.

V.A.Aleshkevich, L.G.Dedenko, V.A.Karavaev (Fizicheskii fakul'tet MGU)
Izdatel'stvo Fizicheskogo fakul'teta MGU, 2001 g. Soderzhanie

Volny na poverhnosti zhidkosti. Gravitacionnye volny. Kapillyarnye volny. Cunami. Vnutrennie volny. Akusticheskie volny bol'shoi amplitudy. Lineinyi i nelineinyi rezhimy rasprostraneniya. Uedinennye volny (solitony).

Volny na poverhnosti zhidkosti. Gravitacionnye volny.

Mnogie iz nas mogut dolgo lyubovat'sya poverhnost'yu morya ili reki, po kotoroi perekatyvayutsya volny. Rozhdennye vetrom, oni rasprostranyayutsya zatem za schet sily tyazhesti. Takie volny nazyvayutsya gravitacionnymi. Chasticy vody sovershayut v nih dvizhenie po krugovym i ellipticheskim traektoriyam ("vverh - vniz" i "vpered - nazad" odnovremenno), poetomu takie volny (kak i volny Lyava) nel'zya otnesti ni k prodol'nym, ni k poperechnym. Gravitacionnye volny obladayut ryadom udivitel'nyh svoistv, k analizu kotoryh my i pristupim.

Pust' po poverhnosti vodoema glubinoi $H$ rasprostranyaetsya vdol' osi Ox poverhnostnaya garmonicheskaya volna

$s(x,t) = s_{0} \sin (\omega t - kx),$

(6.1)

gde $s$ - smeshenie poverhnosti vody vverh ot ravnovesnogo gorizontal'nogo polozheniya, otmechennogo na ris. 6.1 punktirom. Budem schitat', chto $| s| \ll H.$

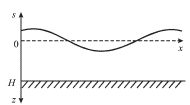Ris. 6.1.

Predpolozhim, chto davlenie zhidkosti na glubine $z$ ravno:

$p(z,x,t) = \rho gz + \delta p(z,x,t),$

(6.2)

gde $\delta p$ - dobavka k gidrostaticheskomu davleniyu $\rho gz,$ obuslovlennaya volnovym dvizheniem poverhnosti. Sdelaem takzhe predpolozhenie, chto

$\delta p(z,x,t) = f(z)\rho gs(x,t).$

(6.3)

Vyrazhenie (6.3) zapisano v priblizhenii, chto vozmushenie davleniya vblizi poverhnosti $(z \to 0)$ opredelyaetsya dopolnitel'nym gidrostaticheskim davleniem $\rho gs,$ svyazannym s izmeneniem urovnya zhidkosti pri rasprostranenii volny:

$\delta p(0,x,t) = \rho gs(x,t),$

(6.4)

prichem s glubinoi eto vozmushenie dolzhno ubyvat'. Sledovatel'no, funkciya $f(z)$ s rostom $z$ takzhe dolzhna ubyvat', pri etom $f(0) = 1.$ Pozzhe my dokazhem, chto predstavlenie vozmusheniya davleniya v vide (6.3) opravdanno.

Dlya opisaniya volnovogo dvizheniya zhidkosti nam neobhodimo, vo-pervyh, dlya zadannoi chastoty $\omega$ naiti $k,$ to est' ustanovit' dispersionnuyu zavisimost' $\omega = \omega (k)$ i, vo-vtoryh, opredelit' vid funkcii $f(z).$ Eto mozhno sdelat', esli s uchetom (6.2) zapisat' uravneniya Eilera dlya dvizheniya neszhimaemoi i nevyazkoi zhidkosti v ploskosti XOZ (sm. uravnenie (3.30) v lekcii po gidrodinamike):

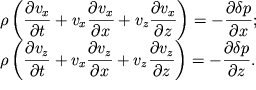$\begin{array}{l} \rho \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \partial v_{x} }}{\displaystyle {\displaystyle \partial t}}} + v_{x} {\displaystyle \frac{\displaystyle {\displaystyle \partial v_{x} }}{\displaystyle {\displaystyle \partial x}}} + v_{z} {\displaystyle \frac{\displaystyle {\displaystyle \partial v_{x} }}{\displaystyle {\displaystyle \partial z}}}} \right) = - {\displaystyle \frac{\displaystyle {\displaystyle \partial \delta p}}{\displaystyle {\displaystyle \partial x}}}; \\ \rho \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \partial v_{z} }}{\displaystyle {\displaystyle \partial t}}} + v_{x} {\displaystyle \frac{\displaystyle {\displaystyle \partial v_{z} }}{\displaystyle {\displaystyle \partial x}}} + v_{z} {\displaystyle \frac{\displaystyle {\displaystyle \partial v_{z} }}{\displaystyle {\displaystyle \partial z}}}} \right) = - {\displaystyle \frac{\displaystyle {\displaystyle \partial \delta p}}{\displaystyle {\displaystyle \partial z}}}. \\ \end{array}$

(6.5)

Pri zapisi (6.5) my predpolagaem, chto dvizhenie chastic po osi Oy otsutstvuet. Uchtem dalee, chto chlenami $v_{x} {\displaystyle \frac{\displaystyle {\displaystyle \partial v_{x} }}{\displaystyle {\displaystyle \partial x}}}, v_{z} {\displaystyle \frac{\displaystyle {\displaystyle \partial v_{z} }}{\displaystyle {\displaystyle \partial z}}}, v_{x} {\displaystyle \frac{\displaystyle {\displaystyle \partial v_{z} }}{\displaystyle {\displaystyle \partial x}}}$ i $v_{z} {\displaystyle \frac{\displaystyle {\displaystyle \partial v_{z} }}{\displaystyle {\displaystyle \partial z}}}$ v silu ih malosti mozhno prenebrech'. Togda poluchaem

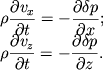$\begin{array}{l} \rho {\displaystyle \frac{\displaystyle {\displaystyle \partial v_{x} }}{\displaystyle {\displaystyle \partial t}}} = - {\displaystyle \frac{\displaystyle {\displaystyle \partial \delta p}}{\displaystyle {\displaystyle \partial x}}}; \\ \rho {\displaystyle \frac{\displaystyle {\displaystyle \partial v_{z} }}{\displaystyle {\displaystyle \partial t}}} = - {\displaystyle \frac{\displaystyle {\displaystyle \partial \delta p}}{\displaystyle {\displaystyle \partial z}}}. \\ \end{array}$

(6.6)

Eti uravneniya dopolnim usloviem neszhimaemosti:

${\displaystyle \frac{\displaystyle {\displaystyle \partial v_{x} }}{\displaystyle {\displaystyle \partial x}}} + {\displaystyle \frac{\displaystyle {\displaystyle \partial v_{z} }}{\displaystyle {\displaystyle \partial z}}} = 0.$

(6.7)

Uravneniya (6.6) i (6.7) pri zadannyh granichnyh usloviyah dayut vozmozhnost' rasschitat' $v_{z}, v_{x}$ i $\delta p$ i, tem samym, poluchit' reshenie zadachi o dvizhenii zhidkosti, vklyuchaya dvizhenie ee poverhnosti.

Prodifferenciruem pervoe iz uravnenii (6.6) po $h,$ a vtoroe - po $z$ :

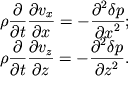$\begin{array}{l} \rho {\displaystyle \frac{\displaystyle {\displaystyle \partial }}{\displaystyle {\displaystyle \partial t}}}{\displaystyle \frac{\displaystyle {\displaystyle \partial v_{x} }}{\displaystyle {\displaystyle \partial x}}} = - {\displaystyle \frac{\displaystyle {\displaystyle \partial ^{2}\delta p}}{\displaystyle {\displaystyle \partial x^{2}}}}; \\ \rho {\displaystyle \frac{\displaystyle {\displaystyle \partial }}{\displaystyle {\displaystyle \partial t}}}{\displaystyle \frac{\displaystyle {\displaystyle \partial v_{z} }}{\displaystyle {\displaystyle \partial z}}} = - {\displaystyle \frac{\displaystyle {\displaystyle \partial ^{2}\delta p}}{\displaystyle {\displaystyle \partial z^{2}}}}. \\ \end{array}$

(6.8)

V levyh chastyah etoi sistemy uravnenii izmenen poryadok differencirovaniya.

Slozhim teper' uravneniya (6.8). Togda s uchetom (6.7) mozhem zapisat':

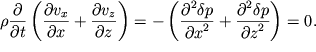$\rho {\displaystyle \frac{\displaystyle {\displaystyle \partial }}{\displaystyle {\displaystyle \partial t}}}\left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \partial v_{x} }}{\displaystyle {\displaystyle \partial x}}} + {\displaystyle \frac{\displaystyle {\displaystyle \partial v_{z} }}{\displaystyle {\displaystyle \partial z}}}} \right) = - \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \partial ^{2}\delta p}}{\displaystyle {\displaystyle \partial x^{2}}}} + {\displaystyle \frac{\displaystyle {\displaystyle \partial ^{2}\delta p}}{\displaystyle {\displaystyle \partial z^{2}}}}} \right) = 0.$

(6.9)

Uravnenie

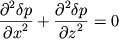${\displaystyle \frac{\displaystyle {\displaystyle \partial ^{2}\delta p}}{\displaystyle {\displaystyle \partial x^{2}}}} + {\displaystyle \frac{\displaystyle {\displaystyle \partial ^{2}\delta p}}{\displaystyle {\displaystyle \partial z^{2}}}} = 0$

(6.10)

yavlyaetsya znamenitym uravneniem Laplasa, ispol'zuemym vo mnogih razdelah fiziki. Poetomu ego reshenie horosho izvestno.

Na poverhnosti vodoema pri $z = 0$ granichnym usloviem yavlyaetsya ravenstvo (6.4), a na dne pri $z = H$ dolzhno vypolnyat'sya uslovie $v_{z} = 0,$ iz kotorogo s uchetom vtorogo uravneniya (6.6) poluchaem:

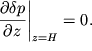${\displaystyle \left. {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \partial \delta p}}{\displaystyle {\displaystyle \partial z}}}} \right|}_{z = H} = 0.$

(6.11)

Podstavim dalee (6.3) v (6.10) i uchtem, chto 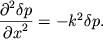${\displaystyle \frac{\displaystyle {\displaystyle \partial ^{2}\delta p}}{\displaystyle {\displaystyle \partial x^{2}}}} = - k^{2}\delta p.$

Togda (6.10) primet vid:

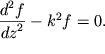${\displaystyle \frac{\displaystyle {\displaystyle d^{2}f}}{\displaystyle {\displaystyle dz^{2}}}} - k^{2}f = 0.$

(6.12)

S metodom resheniya takih uravnenii my poznakomilis' v lekciyah po kolebaniyam. Ispol'zuya podstanovku $f(z) = Ae^{\lambda z},$ poluchaem harakteristicheskoe uravnenie $\lambda ^{2} - k^{2} = 0,$ otkuda $\lambda _{1,2} = \pm k,$ i obshee reshenie (6.12) mozhet byt' zapisano v vide funkcii:

$f(z) = Ae^{kz} + Be^{ - kz},$

(6.13)

pri etom granichnye usloviya dlya $f(z)$ sleduyushie:

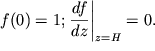$f(0) = 1; {\displaystyle \left. {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle df}}{\displaystyle {\displaystyle dz}}}} \right|}_{z = H} = 0.$

(6.14)

Podstavlyaya (6.13) v (6.14), poluchaem:

$\begin{array}{l} A + B = 1; \\ Ae^{kH} - Be^{ - kH} = 0. \\ \end{array}$

(6.15)

Otsyuda

$f(z) = {\displaystyle \frac{\displaystyle {\displaystyle {\displaystyle \rm ch}\;{\displaystyle \left[ {\displaystyle k(z - H)} \right]}}}{\displaystyle {\displaystyle ch(kH)}}},$

(6.16)

gde funkciya ${\displaystyle \rm ch}\;\alpha = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}(e^{\alpha } + e^{ - \alpha })$ -giperbolicheskii kosinus.

Grafik funkcii $f(z)$ izobrazhen na ris. 6.2. Teper' ostalos' tol'ko opredelit' volnovoe chislo $k,$ vhodyashee v (6.1) i (6.3). Eto mozhno sdelat', esli snachala iz (6.1) naiti vertikal'noe uskorenie chasticy na poverhnosti zhidkosti. Pri etom nado uchest', chto polozhitel'nye znacheniya $v_{z}$ sootvetstvuyut umen'sheniyu $s$ :

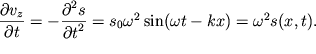${\displaystyle \frac{\displaystyle {\displaystyle \partial v_{z} }}{\displaystyle {\displaystyle \partial t}}} = - {\displaystyle \frac{\displaystyle {\displaystyle \partial ^{2}s}}{\displaystyle {\displaystyle \partial t^{2}}}} = s_{0} \omega ^{2}\sin (\omega t - kx) = \omega ^{2}s(x,t).$

(6.17)

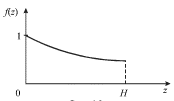Ris. 6.2.

Podstavim (6.17) v levuyu chast' vtorogo uravneniya (6.6), a pravuyu chast' etogo uravneniya zapishem, ispol'zuya predstavlenie (6.3). Togda poluchim

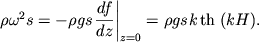$\rho \omega ^{2}s = - \rho gs{\displaystyle \left. {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle df}}{\displaystyle {\displaystyle dz}}}} \right|}_{z = 0} = \rho gs{\displaystyle \kern 1pt} k{\displaystyle \kern 1pt} {\displaystyle \rm th}\;(kH).$

(6.18)

V (6.18) uchteno, chto $({\displaystyle \rm ch}\;\alpha )' = {\displaystyle \rm sh}\;\alpha,\; {\displaystyle \rm th}\;\alpha = {\displaystyle \rm sh}\;\alpha / {\displaystyle \rm ch}\;\alpha.$ Poetomu dispersionnoe sootnoshenie poluchaetsya v vide:

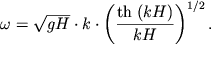$\omega = \sqrt {\displaystyle gH} \cdot k \cdot \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle {\displaystyle \rm th}\;(kH)}}{\displaystyle {\displaystyle kH}}}} \right)^{1 / 2}.$

(6.19)

Oboznachim $c_{0} = \sqrt {\displaystyle gH}.$ Togda

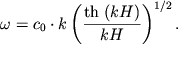$\omega = c_{0} \cdot k\left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle {\displaystyle \rm th}\;(kH)}}{\displaystyle {\displaystyle kH}}}} \right)^{1 / 2}.$

(6.20)

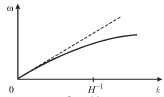
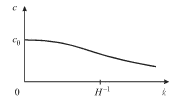
Na ris. 6.3 eta zavisimost' izobrazhena sploshnoi liniei, a punktirom pokazana pryamaya $\omega = c_{0} k.$ Fazovaya skorost' volny $c = \omega / k$ kak funkciya volnovogo chisla pokazana na ris. 6.4.


Ris. 6.3.	Ris. 6.4.

Takim obrazom, poverhnostnye gravitacionnye volny podverzheny sil'noi dispersii. Effekt dispersii yarko vyrazhen u okeanskih voln, zarozhdayushihsya v udalennyh shtormovyh raionah. Poskol'ku dlinnye volny (s men'shim $k$ ) dvizhutsya bystree, chem korotkie, to oni prihodyat k beregam ran'she korotkih na 1-2 dnya.

Effekt dispersii mozhet ispol'zovat'sya pri opredelenii mesta vozniknoveniya voln, proshedshih do tochki nablyudeniya chrezvychaino bol'shie rasstoyaniya. Rasstoyanie ot shtormovogo raiona do mesta, gde volny fiksiruyut, podschityvaetsya po raznosti vremen pribytiya voln raznoi dliny volny i, sledovatel'no, raznoi chastoty. Preobladayushaya chastota pribyvayushih voln rastet vo vremeni, a dlina proidennogo puti nahoditsya po skorosti izmeneniya chastoty. Tak, po ocenke, odin iz paketov voln, nablyudavshihsya v severnoi chasti Tihogo okeana, proshel polovinu okruzhnosti zemnogo shara ot Indiiskogo okeana po duge bol'shogo kruga, prohodyashei yuzhnee Avstralii.

Real'nye volny, kak uzhe govorilos' ran'she, predstavlyayut soboi superpoziciyu voln, ili volnovye pakety, kotorye dvizhutsya s gruppovoi skorost'yu $u = d\omega / dk.$ Skorost' $u$ gruppy men'she, chem skorosti $c = \omega / k$ kazhdoi iz voln v gruppe. Esli rassmatrivat' otdel'nuyu volnu, to mozhno videt', chto ona peremeshaetsya bystree, chem gruppa. Pri dostizhenii fronta gruppy ona zatuhaet, a ee mesto zanimayut volny, dogonyayushie gruppu s tyla.

Fazovaya skorost' volny c, kak sleduet iz (6.20), zavisit ot parametra $kH = 2\pi H / \lambda.$ Poetomu razlichayut volny glubokoi i melkoi vody.

Nazad| Vpered

Publikacii s klyuchevymi slovami: kolebaniya - volny Publikacii so slovami: kolebaniya - volny
Sm. takzhe: Eho iz glubin krasnogo giganta

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

Kolebaniya i volny. Lekcii.

Lekciya 6

Volny na poverhnosti zhidkosti. Gravitacionnye volny.