Astronet > Kolebaniya i volny

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Kolebaniya i volny. Lekcii.

V.A.Aleshkevich, L.G.Dedenko, V.A.Karavaev (Fizicheskii fakul'tet MGU)
Izdatel'stvo Fizicheskogo fakul'teta MGU, 2001 g. Soderzhanie

Esli $kH \gg 1\; (H \gg \lambda ),$ to takie volny nazyvayut volnami glubokoi vody. Vozmusheniya $\delta p$ sosredotocheny v pripoverhnostnom sloe tolshinoi $\sim \lambda$ i ne "chuvstvuyut" prisutstviya dna. Dlya takih voln, s uchetom priblizheniya ${\displaystyle \rm th}\; (kH) \approx 1,$ dispersionnoe sootnoshenie (6.19) primet vid:

$\omega = \sqrt {\displaystyle gk}.$

(6.21)

Takim obrazom, eti volny obladayut sil'noi dispersiei.

Sdelaem nekotorye ocenki. V okeane preobladayut volny s periodom kolebanii $T\sim 10 s.$ Soglasno (6.21) dlina volny $\lambda = 2\pi / k\sim 150 m,$ a fazovaya skorost' $c\sim 15 m/s.$ Takaya skorost' yavlyaetsya tipichnoi, tak kak ona sovpadaet s harakternoi skorost'yu vetra vblizi poverhnosti, generiruyushego volny glubokoi vody.

Esli proanalizirovat' raspredelenie vozmushenii davleniya s glubinoi, opisyvaemoe funkciei $f(z)$ (sm. (6.16)), to mozhno pokazat', chto $f = e^{ - 1}$ pri $z = \lambda / 6 = 25 m.$ Takim obrazom, priblizhenie glubokoi vody spravedlivo v teh mestah, gde glubina $H \geq 25 m.$

Volny melkoi vody.

Pri priblizhenii k beregu glubina $H$ umen'shaetsya, i realizuetsya uslovie $kH \lt 1\; (2\pi H \lt \lambda ).$ Hotya chastota volny ostaetsya prezhnei, odnako dispersionnoe sootnoshenie primet inoi vid:

$\omega = k\sqrt {\displaystyle gH} = kc_{0},$

(6.22)

iz kotorogo sleduet, chto na melkoi vode dispersiya voln otsutstvuet. Skorost' voln $c_{0} = \sqrt {\displaystyle gH}$ umen'shaetsya s glubinoi, i na glubine $H = 1 m$ skorost' $c_{0} \sim 3 m/s,$ a dlina volny pri $T\sim 10 s$ ravna $\lambda = c_{0} T\sim 30 m.$

V neposredstvennoi blizosti k beregu, gde glubina $H$ sravnima s amplitudoi volny $s_{0},$ volna iskazhaetsya - poyavlyayutsya krutye grebni, kotorye dvizhutsya bystree samoi volny i zatem oprokidyvayutsya. Eto proishodit potomu, chto glubina pod grebnem ravna $H + s_{0}$ i prevoshodit glubinu pod vpadinoi $H - s_{0}.$ V rezul'tate kolebaniya chastic volny priobretayut slozhnyi harakter. Po analogii so zvukami muzykal'nyh instrumentov, oscillogrammy kotoryh pokazany v predydushei lekcii, mozhno skazat', chto kolebaniya chastic vody yavlyayutsya superpoziciei kolebanii mnogih chastot, prichem po mere priblizheniya k beregu shirina chastotnogo spektra uvelichivaetsya. S podobnym iskazheniem akusticheskih voln my vstretimsya neskol'ko pozdnee, kogda budem izuchat' nelineinoe rasprostranenie voln konechnoi amplitudy.

Iz privedennoi vyshe klassifikacii gravitacionnyh voln sleduet, chto dlya okeana s glubinoi $H = 5 km$ volny glubokoi vody dolzhny imet' $\lambda \lt 2\pi H\sim 30 km.$ Soglasno (6.21) ih period kolebanii $T = 2\pi / \omega \leq 2 min.$ , a skorost' $c = \lambda / T \leq 250 m/s$ . Dlya kontinental'nogo shel'fa $H\sim 50 m,$ poetomu volnami glubokoi vody budut volny s $\lambda \leq 300 m,\; T \leq 15 s$ i $c \leq 20 m/s.$

S drugoi storony, na glubine H \sim 5 km volny s dlinami voln $\lambda \geq 30 km$ budut volnami melkoi vody. Eti volny imeyut period kolebanii $T \geq 2 min.$ , a ih skorost' $c \geq 250 m/s$ . Takie volny dvigayutsya so skorost'yu reaktivnogo samoleta i mogut peresech' Atlanticheskii okean primerno za 7 chasov.

Harakter dvizheniya chastic zhidkosti.

Rasschitaem skorosti chastic $v_{x}$ i $v_{z},$ kak funkcii koordinat $x, z$ i vremeni $t.$ Eto legko sdelat' iz uravnenii (6.6) s uchetom (6.3), (6.1) i (6.16):

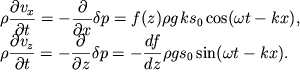$\begin{array}{l} \rho {\displaystyle \frac{\displaystyle {\displaystyle \partial v_{x} }}{\displaystyle {\displaystyle \partial t}}} = - {\displaystyle \frac{\displaystyle {\displaystyle \partial }}{\displaystyle {\displaystyle \partial x}}}\delta p = f(z)\rho g{\displaystyle \kern 1pt} ks_{0} \cos (\omega t - kx), \\ \rho {\displaystyle \frac{\displaystyle {\displaystyle \partial v_{z} }}{\displaystyle {\displaystyle \partial t}}} = - {\displaystyle \frac{\displaystyle {\displaystyle \partial }}{\displaystyle {\displaystyle \partial z}}}\delta p = - {\displaystyle \frac{\displaystyle {\displaystyle df}}{\displaystyle {\displaystyle dz}}}\rho gs_{0} \sin (\omega t - kx). \\ \end{array}$

(6.23)

Otsyuda

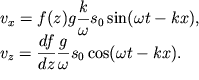$\begin{array}{l} v_{x} = f(z)g{\displaystyle \frac{\displaystyle {\displaystyle k}}{\displaystyle {\displaystyle \omega }}}s_{0} \sin (\omega t - kx), \\ v_{z} = {\displaystyle \frac{\displaystyle {\displaystyle df}}{\displaystyle {\displaystyle dz}}}{\displaystyle \frac{\displaystyle {\displaystyle g}}{\displaystyle {\displaystyle \omega }}}s_{0} \cos (\omega t - kx). \\ \end{array}$

(6.24)

Na ris. 6.5 pokazany vektory skorosti chastic na glubine $z$ i na poverhnosti v fiksirovannyi moment vremeni. Punktirom izobrazheno polozhenie volny cherez malyi promezhutok vremeni. Pod grebnem volny chasticy imeyut sostavlyayushuyu skorosti $v_{x} \gt 0,$ a pod vpadinoi $v_{x} \lt 0.$ Skorost' nekotoroi chasticy A napravlena vniz, i s techeniem vremeni budet izmenyat'sya. Legko ponyat', chto v posleduyushii moment skorost' chasticy A budet takoi, kak u chasticy B v nastoyashii moment, zatem - kak u chasticy C v nastoyashii moment, i tak dalee. Poetomu traektoriya chasticy A budet ellipticheskoi. Po mere uvelicheniya koordinaty $z$ (glubiny pogruzheniya) $v_{z} \to 0,$ ellipsy splyushivayutsya, i pri $z \geq \lambda$ chasticy zhidkosti koleblyutsya prakticheski vdol' osi Ox.

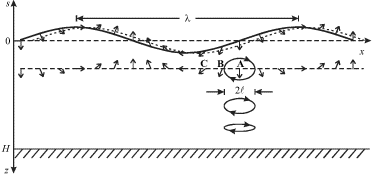Ris. 6.5.

Razmer $\ell$ bol'shoi poluosi ellipsa mozhno ocenit' iz usloviya

$\ell \approx (v_{x} )_{max} T = g{\displaystyle \frac{\displaystyle {\displaystyle k}}{\displaystyle {\displaystyle \omega }}}s_{0} T.$

(6.25)

Sravnim $\ell$ s dlinoi volny $\lambda$ :

${\displaystyle \frac{\displaystyle {\displaystyle \ell }}{\displaystyle {\displaystyle \lambda }}} \approx {\displaystyle \frac{\displaystyle {\displaystyle g}}{\displaystyle {\displaystyle \lambda }}}{\displaystyle \frac{\displaystyle {\displaystyle k}}{\displaystyle {\displaystyle \omega }}}s_{0} T.$

(6.26)

Uchtem, chto $\omega / k = c,\; \lambda = cT,\; c_{0} = \sqrt {\displaystyle gH}$ - skorost' voln melkoi vody. Togda

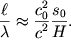${\displaystyle \frac{\displaystyle {\displaystyle \ell }}{\displaystyle {\displaystyle \lambda }}} \approx {\displaystyle \frac{\displaystyle {\displaystyle c_{0}^{2} }}{\displaystyle {\displaystyle c^{2}}}}{\displaystyle \frac{\displaystyle {\displaystyle s_{0} }}{\displaystyle {\displaystyle H}}}.$

(6.27)

Dlya melkoi vody $c = c_{0},$ i

${\displaystyle \frac{\displaystyle {\displaystyle \ell }}{\displaystyle {\displaystyle \lambda }}} = {\displaystyle \frac{\displaystyle {\displaystyle s_{0} }}{\displaystyle {\displaystyle H}}} \ll 1.$

(6.28)

Poskol'ku v etom sluchae $\lambda \sim H,$ to $\ell \sim s_{0},$ t.e. vozrastaet s rostom amplitudy volny $s_{0}.$ No tak kak $s_{0} \ll H,$ to amplituda gorizontal'nyh kolebanii $\ell \ll \lambda.$

Chasticy na poverhnosti glubokoi zhidkosti dvizhutsya po traektoriyam, blizkim k krugovym. Po takim zhe traektoriyam budet dvigat'sya i plavayushee na poverhnosti nebol'shoe telo, naprimer, pritoplennyi poplavok.

Do sih por my predpolagali, chto profil' volny yavlyaetsya sinusoidal'nym, chto vozmozhno tol'ko v tom sluchae, esli amplituda volny ochen' mala po sravneniyu s ee dlinoi. V prirode takim profilem real'no obladayut tol'ko prilivnye volny, dlina kotoryh chrezvychaino velika po sravneniyu s ih vysotoi. Obychnye vetrovye volny imeyut bolee slozhnyi vid. Kak pokazyvayut raschety, chasticy zhidkosti v nih dvizhutsya po okruzhnostyam, radius kotoryh eksponencial'no ubyvaet s glubinoi (sm. ris. 6.6). Sploshnymi liniyami na risunke pokazany linii ravnogo davleniya, lyubaya iz kotoryh mozhet sootvetstvovat' poverhnosti vody pri opredelennoi amplitude volny. Eti linii yavlyayutsya trohoidami - traektoriyami tochek, raspolozhennyh na radiuse mezhdu centrom i obodom kolesa, katyashegosya pod gorizontal'noi pryamoi, raspolozhennoi na vysote $\frac{\displaystyle {\displaystyle \lambda }}{\displaystyle {\displaystyle 2\pi }}$ nad urovnem nevozmushennoi poverhnosti vody. Poetomu takaya volna nazyvaetsya trohoidal'noi i otlichaetsya ot sinusoidal'noi garmonicheskoi volny, zadavaemoi formuloi (6.1). Ochen' blizkimi k trohoidal'nym yavlyayutsya volny posle nastupleniya na more shtilya. Eto tak nazyvaemaya mertvaya zyb'. V chastnom sluchae, kogda radius orbity chasticy, nahodyasheisya na poverhnosti vody, raven ${\displaystyle \frac{\displaystyle {\displaystyle \lambda }}{\displaystyle {\displaystyle 2\pi }}},$ profil' volny imeet vid cikloidy (verhnyaya krivaya na ris. 6.6). Odnako, opyt pokazyvaet, chto cikloidal'naya forma poverhnosti vody mozhet nablyudat'sya tol'ko u stoyachih voln.

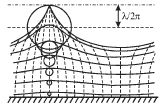Ris. 6.6.

Opytnym putem takzhe ustanovleno, chto u begushih trohoidal'nyh voln ugol mezhdu kasatel'noi k poverhnosti vody i gorizontom ne prevyshaet $\sim 30^\circ.$ Esli ugol skata u grebnya volny prevyshaet eto znachenie, kotoroe sootvetstvuet otnosheniyu amplitudy trohoidal'noi volny k ee dline ${\displaystyle \frac{\displaystyle {\displaystyle s_{0} }}{\displaystyle {\displaystyle \lambda }}} \approx {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 4\pi }}} \approx 0,08,$ to volna teryaet ustoichivost'. Eto yavlenie igraet bol'shuyu rol' v processe zarozhdeniya i razvitiya voln, chto mozhno zametit', nablyudaya za nimi v prisutstvii vetra. Vysokie volny s ostrymi grebeshkami ne mogut prodolzhat' svoi beg, tak kak ih grebni oprokidyvayutsya i razrushayutsya, i volny umen'shayutsya po vysote.

Nazad| Vpered

Publikacii s klyuchevymi slovami: kolebaniya - volny Publikacii so slovami: kolebaniya - volny
Sm. takzhe: Eho iz glubin krasnogo giganta

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

Kolebaniya i volny. Lekcii.

Volny glubokoi vody.

Volny melkoi vody.

Harakter dvizheniya chastic zhidkosti.