Astronet > Kolebaniya i volny

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Kolebaniya i volny. Lekcii.

V.A.Aleshkevich, L.G.Dedenko, V.A.Karavaev (Fizicheskii fakul'tet MGU)
Izdatel'stvo Fizicheskogo fakul'teta MGU, 2001 g. Soderzhanie

Pri analize zavisimosti skorosti ot volnovogo chisla, izobrazhennoi na ris. 6.4, voznikaet vopros: do kakoi velichiny padaet skorost' c pri uvelichenii volnovogo chisla $k$ (ili umen'shenii dliny volny). Opyt pokazyvaet, chto s umen'sheniem dliny volny skorost' dostigaet minimuma, a zatem nachinaet vozrastat'. Eto svyazano s tem, chto pri malom radiuse $R$ krivizny poverhnosti $(R\sim \lambda )$ nachinayut igrat' zametnuyu rol' sily poverhnostnogo natyazheniya. Pod ih deistviem poverhnost' vody stremitsya umen'shit' svoyu ploshad'. Situaciya napominaet rassmotrennuyu ranee, v sluchae s natyanutym rezinovym shnurom. Takie volny nazyvayutsya kapillyarnymi.

Esli pri uvelichenii natyazheniya shnura skorost' rasprostraneniya po nemu voln vozrastala, to pri usilenii roli poverhnostnogo natyazheniya (umen'shenii $\lambda \sim R$ ) skorost' kapillyarnyh voln dolzhna takzhe uvelichivat'sya. Izvestno, chto davlenie pod iskrivlennoi cilindricheskoi poverhnost'yu $p\sim {\displaystyle \frac{\displaystyle {\displaystyle \sigma }}{\displaystyle {\displaystyle R}}},$ gde $\sigma$ - koefficient poverhnostnogo natyazheniya. Esli priblizhenno schitat', chto $\lambda = 2\pi R,$ to po analogii s formuloi dlya skorosti zvuka v gaze (pri $\gamma = 1$ ) mozhno ocenit' fazovuyu skorost' takih voln:

$c_{k} = {\displaystyle \frac{\displaystyle {\displaystyle \omega }}{\displaystyle {\displaystyle k}}} = \sqrt {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle p}}{\displaystyle {\displaystyle \rho }}}} = \sqrt {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \sigma }}{\displaystyle {\displaystyle \rho }}}k}.$

(6.29)

Raschet pokazyvaet, chto formula (6.29) dlya kapillyarnyh voln glubokoi vody okazyvaetsya tochnoi. Uchet konechnosti glubiny vodoema daet dlya etih voln rezul'tat, analogichnyi poluchennomu vyshe dlya gravitacionnyh voln: v formule (6.29) pod kornem dopolnitel'no poyavlyaetsya mnozhitel' ${\displaystyle \rm th}\;(kH).$

Kapillyarnye volny takzhe ispytyvayut dispersiyu, odnako, v otlichie ot gravitacionnyh, ih fazovaya skorost' vozrastaet s uvelicheniem volnovogo chisla $k,$ t.e. s umen'sheniem $\lambda.$ Polezno zapisat' dispersionnoe sootnoshenie (6.29) v vide:

$\omega ^{2} = {\displaystyle \frac{\displaystyle {\displaystyle \sigma }}{\displaystyle {\displaystyle \rho }}}k^{3}.$

(6.30)

Kak sleduet iz etogo sootnosheniya, gruppovaya skorost' $u_{k}$ kapillyarnyh voln glubokoi vody bol'she ih fazovoi skorosti $c_{k}$ v poltora raza: $u_{kap} = {\displaystyle \frac{\displaystyle {\displaystyle d\omega }}{\displaystyle {\displaystyle dk}}} = {\displaystyle \frac{\displaystyle {\displaystyle 3}}{\displaystyle {\displaystyle 2}}}\sqrt {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \sigma }}{\displaystyle {\displaystyle \rho }}}k} = {\displaystyle \frac{\displaystyle {\displaystyle 3}}{\displaystyle {\displaystyle 2}}}c_{kap},$ togda kak dlya gravitacionnyh voln (sm. 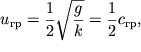(6.21)) $u_{gr} = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}\sqrt {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle g}}{\displaystyle {\displaystyle k}}}} = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}c_{gr},$ t.e. gruppovaya skorost' vdvoe men'she fazovoi. Razlichie gruppovoi i fazovoi skorostei kapillyarnyh voln horosho zametno na poverhnosti vody pri poryvah vetra: vidno, chto melkaya ryab' vnutri gruppy voln dvizhetsya medlennee, chem ves' volnovoi paket.

Esli by my s samogo nachala pri rassmotrenii poverhnostnyh voln uchli kak deistvie sily tyazhesti, tak i poverhnostnoe natyazhenie, my by poluchili dlya voln glubokoi vody odno dispersionnoe sootnoshenie, iz kotorogo formuly (6.21) i (6.30) poluchilis' by predel'nymi perehodami v oblasti malyh i bol'shih $k$ .

Dlya volnovyh chisel $k \gg H^{ - 1}$ my mozhem ob'edinit' (6.21) i (6.30) sleduyushim obrazom:

$\omega = \sqrt {\displaystyle gk + {\displaystyle \frac{\displaystyle {\displaystyle \sigma }}{\displaystyle {\displaystyle \rho }}}k^{3}}.$

(6.31)

Otsyuda skorost' gravitacionno-kapillyarnyh voln glubokoi vody poluchaetsya ravnoi

$c = {\displaystyle \frac{\displaystyle {\displaystyle \omega }}{\displaystyle {\displaystyle k}}} = \sqrt {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle g}}{\displaystyle {\displaystyle k}}} + {\displaystyle \frac{\displaystyle {\displaystyle \sigma }}{\displaystyle {\displaystyle \rho }}}k}.$

(6.32)

Dlya volnovyh chisel $k \ll H^{ - 1}$ (volny melkoi vody) v sootvetstvii s (6.22) skorost' stremitsya k znacheniyu $c_{0} = \sqrt {\displaystyle gH},$ a dlya proizvol'nyh znachenii $k$ v sootvetstvii s (6.20) mozhno zapisat' vyrazhenie dlya skorosti voln sleduyushim obrazom:

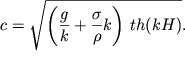$c = \sqrt {\displaystyle \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle g}}{\displaystyle {\displaystyle k}}} + {\displaystyle \frac{\displaystyle {\displaystyle \sigma }}{\displaystyle {\displaystyle \rho }}}k} \right)\,th(kH)}.$

(6.33)

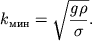Zavisimost' (6.33) skorosti c ot volnovogo chisla $k$ pokazana na ris. 6.7. Vidno, chto skorost' dostigaet minimal'noi velichiny. V sootvetstvii s (6.32) eto proishodit pri $g/k_{min} = \sigma k_{min}/\rho,$ otkuda $k_{min} = \sqrt {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle g\rho }}{\displaystyle {\displaystyle \sigma }}}}.$ Sledovatel'no,

$c_{min} = \sqrt[{\displaystyle 4}]{\displaystyle {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \sigma g}}{\displaystyle {\displaystyle \rho }}}}} \cdot \sqrt {\displaystyle 2}.$

(6.34)

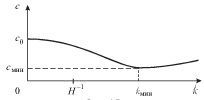Dlya vody $\sigma = 0,073 N/m,\; c_{min} \approx 23,2 sm/s,\; \lambda _{min} = 2\pi /k_{min} \approx 1,73 sm.$

Ris. 6.7.

Takim obrazom, na poverhnosti vody ne mogut sushestvovat' volny, rasprostranyayushiesya so skorost'yu men'she 23 sm/s!

Kapillyarnye volny chasto ispol'zuyutsya dlya opredeleniya koefficienta poverhnostnogo natyazheniya zhidkostei.

Volny cunami.

Krome voln, generiruemyh vetrom, sushestvuyut ochen' dlinnye volny, voznikayushie vo vremya podvodnyh zemletryasenii, ili moretryasenii. Naibolee chasto takie zemletryaseniya proishodyat na dne Tihogo okeana, vdol' dlinnyh cepei Kuril'skih i Yaponskih ostrovov. Gromadnye volny, voznikayushie pri moshnom tolchke, imeyut vysotu $s_{0} \sim 10 - 15 m$ i $\lambda \sim 10^{3} km.$ Dostigaya berega, oni smyvayut ne tol'ko goroda i derevni, no i rastitel'nost' vmeste s pochvoi. Bol'shie bedstviya oni prichinyayut naseleniyu Yaponii, kotoroe dalo im nazvanie "cunami" (po-yaponski - "bol'shaya volna v gavani").

Interesny svedeniya o velichinah deformacii dna okeana vo vremya zemletryasenii. V 1922 godu yaponskie gidrografy sdelali promery glubin v zalive Sagami, nedaleko ot Tokio, a cherez god - 1 sentyabrya 1923 goda - tam proizoshlo katastroficheskoe zemletryasenie. Povtornyi promer glubin posle zemletryaseniya pokazal, chto izmeneniya rel'efa dna proizoshli na ploshadi okolo 150 km², pri etom odni chasti dna podnyalis' mestami na 230 m, a drugie opustilis' do 400 m. Podnyavshayasya chast' dna vytolknula gromadnyi ob'em vody, kotoryi po ocenkam sostavil velichinu $V\sim 23 km^{3}.$ V rezul'tate takogo tolchka obrazovalsya ogromnyi vodyanoi holm (uedinennaya volna), kotoryi pri rasprostranenii vyzval pod'em urovnya vody u beregov Yaponii v raznyh mestah ot 3,3 do 10 m.

Vnutrennie gravitacionnye i inye volny.

Naryadu s poverhnostnymi gravitacionnymi i kapillyarnymi volnami v okeane sushestvuet mnozhestvo drugih vidov voln, kotorye igrayut vazhnuyu rol' v dinamike okeana. Okean, v otlichie ot ideal'noi zhidkosti, stratificirovan - to est' ego vody ne yavlyayutsya odnorodnymi, a izmenyayutsya po plotnosti s glubinoi. Eto raspredelenie obuslovleno potokami energii (tepla) i veshestva. V uproshennom vide okean mozhno predstavit' sostoyashim iz dvuh sloev vody: sverhu lezhit bolee legkaya (teplaya ili menee solenaya), snizu - bolee plotnaya (bolee solenaya ili holodnaya). Podobno tomu kak poverhnostnye volny sushestvuyut na granice voda-vozduh, na granice razdela vod raznoi plotnosti budut sushestvovat' vnutrennie gravitacionnye volny. Amplituda voln etogo tipa v okeane mozhet dostigat' sotni metrov, dlina volny - mnogih kilometrov, no kolebaniya vodnoi poverhnosti pri etom nichtozhny. Vnutrennie volny proyavlyayutsya na poverhnosti okeana, vozdeistvuya na harakteristiki poverhnostnyh voln, pereraspredelyaya poverhnostno-aktivnye veshestva. Po etim proyavleniyam oni i mogut byt' obnaruzheny na poverhnosti okeana. Tak kak poverhnostnye gravitacionno-kapillyarnye volny i poverhnostno-aktivnye veshestva sil'no vliyayut na koefficient otrazheniya elektromagnitnyh, v tom chisle svetovyh voln, vnutrennie volny horosho obnaruzhivayutsya distancionnymi metodami, naprimer, oni vidny iz kosmosa. Vnutrennie volny po sravneniyu s obychnymi poverhnostnymi gravitacionnymi volnami obladayut ryadom udivitel'nyh svoistv. Naprimer, gruppovaya skorost' vnutrennih voln perpendikulyarna fazovoi, ugol otrazheniya vnutrennih voln ot otkosa ne raven uglu padeniya.

Pri rassmotrenii krupnomasshtabnyh yavlenii v Mirovom okeane neobhodimo uchityvat' effekty vrasheniya Zemli, izmenenie glubiny i nalichie bokovyh granic. Sila Koriolisa yavlyaetsya prichinoi vozniknoveniya inercionnyh, ili giroskopicheskih voln. Izmeneniya potencial'noi zavihrennosti vsledstvie izmeneniya geograficheskoi shiroty i glubiny okeana obuslavlivayut vozniknovenie planetarnyh voln Rossbi. Bokovye granicy i izmenenie glubiny na shel'fe privodyat k sushestvovaniyu neskol'kih tipov beregovyh zahvachennyh voln - shel'fovyh, kraevyh, Kel'vina, topograficheskih voln Rossbi.

Krupnomasshtabnye volny tipa voln Rossbi, Kel'vina i dr. okazyvayut sushestvennoe vliyanie na termogidrodinamiku okeana, vzaimodeistvie atmosfery i okeana, klimat i pogodu. Svoistva mnogih iz etih voln sushestvenno otlichayutsya ot svoistv poverhnostnyh gravitacionnyh voln. Naprimer, volny Kel'vina lokalizovany v uzkoi shel'fovoi zone, rasprostranyayutsya v severnom polusharii vdol' berega protiv chasovoi strelki. Ekvatorial'nye volny Rossbi, imeya prostranstvennye masshtaby v sotni kilometrov, lokalizuyutsya vdol' ekvatora i proyavlyayutsya ne v izmenenii urovnya, a prezhde vsego v forme vihrevyh techenii.

Nazad| Vpered

Publikacii s klyuchevymi slovami: kolebaniya - volny Publikacii so slovami: kolebaniya - volny
Sm. takzhe: Eho iz glubin krasnogo giganta

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

Kolebaniya i volny. Lekcii.

Kapillyarnye volny.

Volny cunami.

Vnutrennie gravitacionnye i inye volny.