Astronet > Kolebaniya i volny

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Kolebaniya i volny. Lekcii.

V.A.Aleshkevich, L.G.Dedenko, V.A.Karavaev (Fizicheskii fakul'tet MGU)
Izdatel'stvo Fizicheskogo fakul'teta MGU, 2001 g. Soderzhanie

Rasprostranenie akusticheskih voln konechnoi amplitudy.

Esli vozmusheniya plotnosti $\delta \rho$ i davleniya $\delta p$ v akusticheskoi volne ne yavlyayutsya ischezayushe malymi po sravneniyu s ravnovesnymi znacheniyami $\rho _{0}$ i $p_{0},$ to govoryat, chto volna imeet konechnuyu amplitudu. Obychno takie volny obladayut vysokoi intensivnost'yu, i dlya opisaniya ih rasprostraneniya neobhodimo reshat' nelineinye uravneniya gidrodinamiki. Analizom rasprostraneniya voln konechnoi amplitudy zanimaetsya otdel'naya nauka, nazyvaemaya nelineinoi akustikoi. V nashih lekciyah my ogranichimsya lish' nebol'shim ob'emom svedenii iz nelineinoi akustiki.

Pust' v gaze vdol' osi Ox rasprostranyaetsya moshnaya akusticheskaya volna. Esli prenebrech' vyazkost'yu gaza, to odnomernoe dvizhenie chastic vdol' etoi osi budet opisyvat'sya uravneniem Eilera i uravneniem nepreryvnosti:

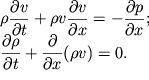$\begin{array}{l} \rho {\displaystyle \frac{\displaystyle {\displaystyle \partial v}}{\displaystyle {\displaystyle \partial t}}} + \rho v{\displaystyle \frac{\displaystyle {\displaystyle \partial v}}{\displaystyle {\displaystyle \partial x}}} = - {\displaystyle \frac{\displaystyle {\displaystyle \partial p}}{\displaystyle {\displaystyle \partial x}}}; \\ {\displaystyle \frac{\displaystyle {\displaystyle \partial \rho }}{\displaystyle {\displaystyle \partial t}}} + {\displaystyle \frac{\displaystyle {\displaystyle \partial }}{\displaystyle {\displaystyle \partial x}}}(\rho v) = 0. \\ \end{array}$

(6.35)

Slozhnost' resheniya etoi sistemy uravnenii sostoit v tom, chto v ih levyh chastyah soderzhatsya nelineinye chleny. Obychno etu nelineinost' nazyvayut kinematicheskoi nelineinost'yu. Poskol'ku uravneniya (6.35) soderzhat tri neizvestnye funkcii $\rho (x,t),\; p(x,t)$ i $v(x,t),$ to neobhodimo ih dopolnit' tret'im uravneniem, svyazyvayushim $p$ i $\rho.$ Dlya gaza ono, kak uzhe otmechalos' ranee, yavlyaetsya uravneniem adiabaty:

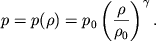$p = p(\rho ) = p_{0} \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \rho }}{\displaystyle {\displaystyle \rho _{0} }}}} \right)^{\gamma }.$

(6.36)

Predstavim $p$ i $\rho$ v vide:

$p = p_{0} + \delta p; \quad \rho = \rho _{0} + \delta \rho.$

(6.37)

Zatem podstavim (6.37) v (6.36):

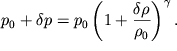$p_{0} + \delta p = p_{0} \left( {\displaystyle 1 + {\displaystyle \frac{\displaystyle {\displaystyle \delta \rho }}{\displaystyle {\displaystyle \rho _{0} }}}} \right)^{\gamma }.$

(6.38)

Polagaya, chto ${\displaystyle \left| {\displaystyle \delta \rho / \rho _{0} } \right|} \lt 1,$ razlozhim pravuyu chast' (6.38) v ryad:

$p_{0} + \delta p = p_{0} {\displaystyle \left[ {\displaystyle 1 + \gamma {\displaystyle \frac{\displaystyle {\displaystyle \delta \rho }}{\displaystyle {\displaystyle \rho _{0} }}} + {\displaystyle \frac{\displaystyle {\displaystyle \gamma \left( {\displaystyle \gamma - 1} \right)}}{\displaystyle {\displaystyle 2}}}\left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \delta \rho }}{\displaystyle {\displaystyle \rho _{0} }}}} \right)^{2} + \ldots} \right]}.$

(6.39)

Prenebregaya chlenami, imeyushimi poryadok malosti $(\delta \rho / \rho _{0} )^{3}$ i vyshe, okonchatel'no zapishem uravnenie adiabaty v vide:

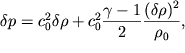$\delta p = c_{0}^{2} \delta \rho + c_{0}^{2} {\displaystyle \frac{\displaystyle {\displaystyle \gamma - 1}}{\displaystyle {\displaystyle 2}}}{\displaystyle \frac{\displaystyle {\displaystyle (\delta \rho )^{2}}}{\displaystyle {\displaystyle \rho _{0} }}},$

(6.40)

gde $c_{0}^{2} = \gamma {\displaystyle \frac{\displaystyle {\displaystyle p_{0} }}{\displaystyle {\displaystyle \rho _{0} }}}.$

Vtoroi chlen v pravoi chasti (6.40) nachinaet davat' zametnyi vklad pri sil'nom szhatii (razrezhenii), poetomu svyaz' mezhdu vozmusheniyami davleniya $\delta p$ i plotnosti $\delta \rho$ stanovitsya nelineinoi. Eta nelineinost' obuslovlena nelineinost'yu sil mezhmolekulyarnogo vzaimodeistviya i nazyvaetsya fizicheskoi nelineinost'yu. Ona vmeste s kinematicheskoi nelineinost'yu mozhet kardinal'no povliyat' na harakter rasprostraneniya intensivnyh akusticheskih voln.

Pereidem teper' k ustanovleniyu osnovnyh zakonomernostei takogo rasprostraneniya. Dlya etogo podstavim (6.37) v uravneniya (6.35). Togda poluchim:

$\begin{array}{l} (\rho _{0} + \delta \rho ){\displaystyle \frac{\displaystyle {\displaystyle \partial v}}{\displaystyle {\displaystyle \partial t}}} + (\rho _{0} + \delta \rho )v{\displaystyle \frac{\displaystyle {\displaystyle \partial v}}{\displaystyle {\displaystyle \partial x}}} = - {\displaystyle \frac{\displaystyle {\displaystyle \partial \delta p}}{\displaystyle {\displaystyle \partial x}}}; \\ {\displaystyle \frac{\displaystyle {\displaystyle \partial \delta \rho }}{\displaystyle {\displaystyle \partial t}}} + {\displaystyle \frac{\displaystyle {\displaystyle \partial }}{\displaystyle {\displaystyle \partial x}}}[(\rho _{0} + \delta \rho )v] = 0. \\ \end{array}$

(6.41)

Chtoby pomoch' chitatelyu preodolet' psihologicheskii bar'er, svyazannyi s analizom sistemy nelineinyh uravnenii (6.40) - (6.41), my pokazhem vnachale, kak iz etih uravnenii mozhno legko poluchit' volnovoe uravnenie, opisyvayushee lineinyi rezhim rasprostraneniya voln, izuchennyi podrobno ranee.

Lineinyi rezhim.

$(| \delta \rho |\ll \rho _{0},\; | \delta p| \ll p_{0} ).$

Uderzhim v uravneniyah (6.41) tol'ko lineinye chleny. Togda poluchim

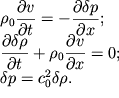$\begin{array}{l} \rho _{0} {\displaystyle \frac{\displaystyle {\displaystyle \partial v}}{\displaystyle {\displaystyle \partial t}}} = - {\displaystyle \frac{\displaystyle {\displaystyle \partial \delta p}}{\displaystyle {\displaystyle \partial x}}}; \\ {\displaystyle \frac{\displaystyle {\displaystyle \partial \delta \rho }}{\displaystyle {\displaystyle \partial t}}} + \rho _{0} {\displaystyle \frac{\displaystyle {\displaystyle \partial v}}{\displaystyle {\displaystyle \partial x}}} = 0; \\ \delta p = c_{0}^{2} \delta \rho. \\ \end{array}$

(6.42)

Isklyuchim dve neizvestnye funkcii, naprimer, $\delta \rho$ i $\delta p.$ Dlya etogo prodifferenciruem pervoe uravnenie po vremeni $t,$ a vtoroe - domnozhim na $c_{0}^{2}$ i prodifferenciruem po koordinate $h,$ a zatem vychtem odno uravnenie iz drugogo. S uchetom tret'ego uravneniya chleny, soderzhashie $\delta \rho$ i $\delta p,$ sokratyatsya, i my poluchim izvestnoe nam volnovoe uravnenie

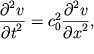${\displaystyle \frac{\displaystyle {\displaystyle \partial ^{2}v}}{\displaystyle {\displaystyle \partial t^{2}}}} = c_{0}^{2} {\displaystyle \frac{\displaystyle {\displaystyle \partial ^{2}v}}{\displaystyle {\displaystyle \partial x^{2}}}},$

(6.43)

opisyvayushee rasprostranenie bez iskazhenii vdol' osi Ox so skorost'yu $c_{0}$ volny gidrodinamicheskoi skorosti.

Analogichnym obrazom mozhno poluchit' volnovye uravneniya dlya vozmushenii davleniya $\delta p$ i plotnosti $\delta \rho.$ Ne ostanavlivayas' dalee na resheniyah takih uravnenii (my eto sdelali detal'no v predydushih lekciyah) pereidem teper' k nelineinomu rezhimu rasprostraneniya voln konechnoi amplitudy.

Nelineinyi rezhim.

$(| \delta \rho | \lt \rho _{0},\; | \delta p| \lt p_{0} ).$

Vnachale popytaemsya kachestvenno opisat' osnovnye cherty nelineinogo rasprostraneniya voln, ne pribegaya k matematike. Naibolee prosto eto sdelat', esli obratit'sya k vliyaniyu fizicheskoi nelineinosti (formula 6.36). Esli vspomnit', chto skorost' zvuka $c = \sqrt {\displaystyle dp / d\rho },$ to legko ponyat', chto razlichnye chasti volny mogut dvigat'sya s raznymi skorostyami.

Na ris. 6.8 izobrazhena zavisimost' (6.36) i dlya treh znachenii plotnosti $\rho _{0}, \rho _{1}$ i $\rho _{2}$ provedeny kasatel'nye k grafiku funkcii $p = p(\rho ),$ uglovye koefficienty kotoryh ravny kvadratu skorosti rasprostraneniya volny. Iz etogo grafika mozhno sdelat' kachestvennyi vyvod o tom, chto chem vyshe plotnost' uchastka volny, tem bol'she ego skorost'.

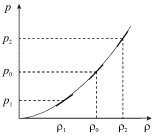Ris. 6.8.

Esli, naprimer, garmonicheskaya volna (volna plotnosti) rasprostranyaetsya vdol' osi Ox (ris. 6.9), to iz-za razlichiya skorostei ee raznyh chastei ona budet postepenno menyat' svoyu formu. Na risunke dlya prostoty pokazany lish' tri skorosti $c_{1} = {\displaystyle \left. {\displaystyle \sqrt {\displaystyle \left( {\displaystyle dp / d\rho } \right)} } \right|}_{\rho _{1} },\; c_{0} = {\displaystyle \left. {\displaystyle \sqrt {\displaystyle \left( {\displaystyle dp / d\rho } \right)} } \right|}_{\rho _{0} }$ i $c_{2} = {\displaystyle \left. {\displaystyle \sqrt {\displaystyle \left( {\displaystyle dp / d\rho } \right)} } \right|}_{\rho _{2} }.$

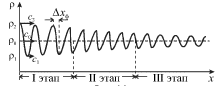Ris. 6.9.

Kak pokazyvaet opyt, rasprostranenie volny mozhno oharakterizovat' tremya etapami.

Na I etape volna transformiruetsya v piloobraznuyu, obladayushuyu skachkom plotnosti $\rho$ (a takzhe davleniya $p$ i skorosti $v$ ). Eta piloobraznaya volna priobretaet udarnyi front, shirina kotorogo $\Delta x_{f}$ po mere rasprostraneniya umen'shaetsya i dostigaet velichiny poryadka dliny svobodnogo probega molekul gaza.

Na II etape proishodit nelineinoe zatuhanie volny dazhe pri ochen' maloi vyazkosti i teploprovodnosti sredy. Etot, na pervyi vzglyad, neozhidannyi effekt svyazan s perehodom v teplo chasti kineticheskoi energii molekul, obladayushih gidrodinamicheskimi skorostyami $v$ . Eti molekuly pod deistviem perepadov davleniya na dline svobodnogo probega priobretayut kineticheskuyu energiyu, kotoraya zatem perehodit v teplo pri neuprugih stolknoveniyah. Prosteishii raschet pokazyvaet, chto energiya, pereshedshaya v teplo, budet sushestvenno bol'she, chem na I etape, kogda na shirine $\Delta x_{f}$ proishodili mnogochislennye stolknoveniya. Estestvenno, chto eta teplovaya energiya zaimstvuetsya u rasprostranyayusheisya volny.

III etap svyazan s vozrastayushim vliyaniem vyazkosti i teploprovodnosti, kotorye osobenno sil'ny v oblastyah bol'shih perepadov skorosti i temperatury (vsledstvie lokal'nogo adiabaticheskogo nagreva ili ohlazhdeniya pri kolebaniyah gaza). Rezkie perepady skorosti privodyat k vozrastaniyu sil vyazkosti, a perepady temperatury na masshtabah poryadka dliny volny vlekut ottok tepla iz bolee nagretyh oblastei v menee nagretye. Iz-za etih prichin chast' energii volny perehodit v teplo, i ee amplituda umen'shaetsya. Poskol'ku pogloshenie zvuka proporcional'no kvadratu chastoty, bystree zatuhayut volny vysshih chastot, i volna transformiruetsya v garmonicheskuyu volnu s ishodnoi (nachal'noi) chastotoi.

Nazad| Vpered

Publikacii s klyuchevymi slovami: kolebaniya - volny Publikacii so slovami: kolebaniya - volny
Sm. takzhe: Eho iz glubin krasnogo giganta

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce