Astronet > Kolebaniya i volny

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Kolebaniya i volny. Lekcii.

V.A.Aleshkevich, L.G.Dedenko, V.A.Karavaev (Fizicheskii fakul'tet MGU)
Izdatel'stvo Fizicheskogo fakul'teta MGU, 2001 g. Soderzhanie

Rassuzhdeniya, privedennye vyshe, nosyat kachestvennyi harakter. Dlya kolichestvennogo opisaniya nelineinogo rasprostraneniya voln my ispol'zuem naibolee uproshennyi podhod k analizu sistemy nelineinyh uravnenii (6.40) - (6.41). Ogovorimsya srazu, chto poskol'ku uravneniya Eilera opisyvayut povedenie nevyazkoi sredy, to my smozhem proanalizirovat' rasprostranenie volny lish' na pervyh dvuh etapah.

Perepishem uravneniya v (6.41) v vide:

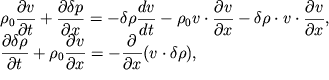$\begin{array}{l} \rho _{0} {\displaystyle \frac{\displaystyle {\displaystyle \partial v}}{\displaystyle {\displaystyle \partial t}}} + {\displaystyle \frac{\displaystyle {\displaystyle \partial \delta p}}{\displaystyle {\displaystyle \partial x}}} = - \delta \rho {\displaystyle \frac{\displaystyle {\displaystyle dv}}{\displaystyle {\displaystyle dt}}} - \rho _{0} v \cdot {\displaystyle \frac{\displaystyle {\displaystyle \partial v}}{\displaystyle {\displaystyle \partial x}}} - \delta \rho \cdot v \cdot {\displaystyle \frac{\displaystyle {\displaystyle \partial v}}{\displaystyle {\displaystyle \partial x}}}, \\ {\displaystyle \frac{\displaystyle {\displaystyle \partial \delta \rho }}{\displaystyle {\displaystyle \partial t}}} + \rho _{0} {\displaystyle \frac{\displaystyle {\displaystyle \partial v}}{\displaystyle {\displaystyle \partial x}}} = - {\displaystyle \frac{\displaystyle {\displaystyle \partial }}{\displaystyle {\displaystyle \partial x}}}(v \cdot \delta \rho ), \\ \end{array}$

(6.44)

gde vse nelineinye chleny, po poryadku velichiny men'shie lineinyh, pereneseny v pravye chasti uravnenii.

S uchetom malosti nelineinyh chlenov dlya etih uravnenii v nelineinoi akustike razrabotany priblizhennye metody resheniya, smysl kotoryh sostoit v poluchenii znachitel'no bolee prostyh uravnenii, imeyushih v ryade sluchaev neslozhnye analiticheskie resheniya. Odno iz takih uravnenii my seichas i poluchim, odnako sdelaem eto predel'no prosto. Dlya etogo, vo-pervyh, my ogranichimsya vnachale lish' kinematicheskoi nelineinost'yu, a, vo-vtoryh, budem predpolagat', chto mezhdu skorost'yu $v$ i vozmusheniem $\delta \rho$ sushestvuet takaya zhe svyaz', kak i v lineinom rezhime:

$- \varepsilon = {\displaystyle \frac{\displaystyle {\displaystyle \delta p}}{\displaystyle {\displaystyle p_{0} }}} = {\displaystyle \frac{\displaystyle {\displaystyle \delta \rho }}{\displaystyle {\displaystyle \rho _{0} }}} = {\displaystyle \frac{\displaystyle {\displaystyle v}}{\displaystyle {\displaystyle c_{0} }}},$

(6.45)

gde $\varepsilon$ - otnositel'naya deformaciya elementarnogo ob'ema gaza ( $\varepsilon \lt 0$ pri szhatii i $\varepsilon \gt 0$ pri razrezhenii). Eta svyaz' pozvolyaet nam ogranichit'sya odnim iz dvuh uravnenii gidrodinamiki. Predpochtitel'nee, naprimer, vospol'zovat'sya bolee prostym uravneniem nepreryvnosti. Pri podstanovke vo vtoroe uravnenie (6.44) vozmusheniya plotnosti $\delta \rho,$ proporcional'nogo, soglasno (6.45), gidrodinamicheskoi skorosti v, poluchaem nelineinoe uravnenie:

${\displaystyle \frac{\displaystyle {\displaystyle \partial v}}{\displaystyle {\displaystyle \partial t}}} + c_{0} {\displaystyle \frac{\displaystyle {\displaystyle \partial v}}{\displaystyle {\displaystyle \partial x}}} = - 2v{\displaystyle \frac{\displaystyle {\displaystyle \partial v}}{\displaystyle {\displaystyle \partial x}}}.$

(6.46)

Zametim, chto v lineinom rezhime, kogda pravaya chast' uravneniya ravna nulyu, ego resheniem yavlyaetsya lyubaya funkciya vida:

$v(x,t) = f(t - x / c_{0} ),$

(6.47)

opisyvayushaya begushuyu so skorost'yu $c_{0}$ bez iskazheniya vdol' osi Ox akusticheskuyu volnu.

V nelineinom rezhime situaciya uslozhnyaetsya. V samom dele, perepishem uravnenie (6.46) v vide

${\displaystyle \frac{\displaystyle {\displaystyle \partial v}}{\displaystyle {\displaystyle \partial t}}} + (c_{0} + 2v){\displaystyle \frac{\displaystyle {\displaystyle \partial v}}{\displaystyle {\displaystyle \partial x}}} = 0.$

(6.48)

Otsyuda vidno, chto skorost' uchastka volny ravna

$c = c_{0} + 2v$

(6.49)

i zavisit ot gidrodinamicheskoi skorosti chastic.

Dlya fragmenta garmonicheskoi volny gidrodinamicheskoi skorosti, izobrazhennogo na ris. 6.10, eto oznachaet, chto sinusoidal'noe raspredelenie skorosti vdol' osi Ox transformiruetsya v piloobraznoe. Sledovatel'no, oba mehanizma nelineinosti sposobstvuyut transformacii garmonicheskoi volny v piloobraznuyu.

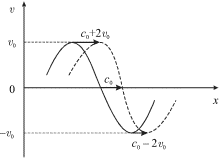Ris. 6.10.

Esli by my s samogo nachala uchli deistvie oboih mehanizmov nelineinosti, to iz uravnenii (6.44) i (6.40) my by poluchili uravnenie

${\displaystyle \frac{\displaystyle {\displaystyle \partial v}}{\displaystyle {\displaystyle \partial t}}} + (c_{0} + \beta v){\displaystyle \frac{\displaystyle {\displaystyle \partial v}}{\displaystyle {\displaystyle \partial x}}} = 0,$

(6.50)

gde $\beta = (\gamma + 1) / 2$ - nelineinyi parametr, otrazhayushii deistvie oboih mehanizmov nelineinosti. Spravedlivosti radi otmetim, chto formula (6.49) ne yavlyaetsya tochnoi, poskol'ku v otsutstvie fizicheskoi nelineinosti $(\gamma = 1)$ nelineinyi parametr $\beta = 1,$ i na samom dele $c = c_{0} + v.$ Eto svyazano s tem, chto my ispol'zovali svyaz' v vide (6.45), kotoraya dlya voln konechnoi amplitudy ne yavlyaetsya vernoi.

Po analogii s (6.47) my mozhem zapisat' reshenie uravneniya (6.50) v vide:

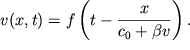$v(x,t) = f\left( {\displaystyle t - {\displaystyle \frac{\displaystyle {\displaystyle x}}{\displaystyle {\displaystyle c_{0} + \beta v}}}} \right).$

(6.51)

Eto reshenie opisyvaet evolyuciyu prostyh (Rimanovyh) voln. Teper' ne sostavlyaet truda kolichestvenno opisat' transformaciyu garmonicheskoi volny v piloobraznuyu.

Pust' na vhode v sredu (pri $x = 0$ )

$v(0,t) = f(t) = v_{0} \sin \omega t.$

(6.52)

Togda na rasstoyanii $x$

$v = v_{0} \sin {\displaystyle \left[ {\displaystyle \omega \left( {\displaystyle \tau + {\displaystyle \frac{\displaystyle {\displaystyle \beta }}{\displaystyle {\displaystyle c_{0}^{2} }}}x \cdot v} \right)} \right]}.$

(6.53)

Zdes' $\tau = t - x / c_{0}$ - tak nazyvaemoe lokal'noe vremya, otschityvaemoe nablyudatelem, nahodyashimsya na rasstoyanii $x$ ot nachala koordinat, ot momenta vremeni $x/c_{0}.$

Dlya postroeniya grafika zavisimosti (6.53) perepishem ee v yavnom vide

$\omega \tau = \arcsin {\displaystyle \frac{\displaystyle {\displaystyle v}}{\displaystyle {\displaystyle v_{0} }}} - {\displaystyle \frac{\displaystyle {\displaystyle x}}{\displaystyle {\displaystyle \ell _{nl} }}} \cdot {\displaystyle \frac{\displaystyle {\displaystyle v}}{\displaystyle {\displaystyle v_{0} }}},$

(6.54)

gde

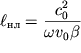$\ell _{nl} = {\displaystyle \frac{\displaystyle {\displaystyle c_{0}^{2} }}{\displaystyle {\displaystyle \omega v_{0} \beta }}}$

(6.55)

harakternoe rasstoyanie, na kotorom razvivaetsya znachitel'noe nelineinoe iskazhenie volny. Eto rasstoyanie sokrashaetsya s rostom amplitudy $v_{0}$ ishodnoi volny i nelineinogo parametra.

Na ris. 6.11 izobrazheny raspredeleniya skorosti v predelah odnogo perioda kolebanii dlya volny na rasstoyaniyah $x = 0\, (1);\; x \lt \ell _{nl}\, (2);\; x \gt \ell _{nl}\, (3).$ Iz etih krivyh vidno, chto sinusoidal'naya volna prevrashaetsya postepenno v piloobraznuyu, a pri $x \gt \ell _{nl}$ v profile volny poyavlyaetsya neodnoznachnost'. Eta neodnoznachnost' ne imeet fizicheskogo smysla i voznikla lish' iz-za prenebrezheniya vyazkost'yu gaza. V deistvitel'nosti pri $\omega \tau = 0$ skorost' ispytyvaet skachok, ili razryv (ot velichiny skorosti v tochke A do velichiny skorosti v tochke V). Polozhenie udarnogo fronta zadaetsya liniei AV, kotoruyu provodyat tak, chtoby zashtrihovannye ploshadi sverhu i snizu ot AV byli by odinakovy (v rassmatrivaemom sluchae AV sovpadaet s os'yu Oy). Takim postroeniem avtomaticheski uchityvaetsya nelineinoe zatuhanie volny. Rasstoyanie $\ell _{nl} ,$ kak netrudno teper' ponyat', yavlyaetsya rasstoyaniem, na kotorom u volny poyavlyayutsya razryvy skorosti $v,$ plotnosti $\rho$ i davleniya $\delta p.$ K sozhaleniyu, bez ucheta vyazkosti shirina udarnogo fronta poluchilas' ravnoi nulyu. V real'noi situacii ona konechna i vozrastaet s uvelicheniem vyazkosti.

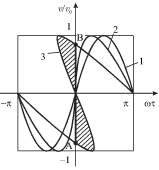Ris. 6.11.

Uchet vyazkosti pozvolyaet opisat' III etap rasprostraneniya, odnako eto vyhodit za ramki nashego kursa.

Govorya ob obrazovanii udarnogo fronta v konce I etapa i posleduyushem nelineinom zatuhanii na II etape, my ne dolzhny zabyvat' o nalichii obychnogo (lineinogo) poglosheniya volny vsledstvie vyazkosti sredy. Eto pogloshenie harakterizuetsya koefficientom $\alpha$ (sm. formulu (5.19)) i zavisit ot chastoty. Amplituda volny pri lineinom pogloshenii umen'shaetsya po eksponencial'nomu zakonu uzhe na I etape: $v_{0} (x) = v_{0} e^{ - x / \ell _{z} },$ gde $\ell _{z} = \alpha ^{ - 1}$ harakternoe rasstoyanie, harakterizuyushee pogloshenie zvuka. Estestvenno, chto umen'shenie amplitudy $v_{0}$ "pritormazhivaet" process iskazheniya profilya volny. Esli pogloshenie takovo, chto $\ell _{z} \lt \ell _{nl},$ to nelineinoe iskazhenie mozhet i ne proyavlyat'sya vovse.

V akustike otnoshenie

$\rm Re} = \ell _{z} / \ell _{nl$

(6.56)

nazyvayut akusticheskim chislom Reinol'dsa. Esli ${\displaystyle \rm Re} \gt 10,$ to volna schitaetsya moshnoi, i dlya nee imeet mesto nelineinoe iskazhenie. Pri ${\displaystyle \rm Re} \lt 1$ volna slabaya, i nelineinoe iskazhenie podavleno obychnym lineinym poglosheniem.

Esli uchest' dalee, chto amplituda skorosti $v_{0}$ svyazana s amplitudoi vozmusheniya davleniya $(\delta p)_{0}$ akusticheskim zakonom Oma, to nelineinaya dlina budet obratno proporcional'na velichine $(\delta p)_{0}$ :

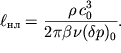$\ell _{nl} = {\displaystyle \frac{\displaystyle {\displaystyle \rho \,c_{0}^{3} }}{\displaystyle {\displaystyle 2\pi \beta \nu (\delta p)_{0} }}}.$

(6.57)

Sledovatel'no, vyrazhenie dlya akusticheskogo chisla Reinol'dsa primet vid:

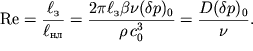${\displaystyle \rm Re} = {\displaystyle \frac{\displaystyle {\displaystyle \ell _{z} }}{\displaystyle {\displaystyle \ell _{nl} }}} = {\displaystyle \frac{\displaystyle {\displaystyle 2\pi \ell _{z} \beta \nu (\delta p)_{0} }}{\displaystyle {\displaystyle \rho \,c_{0}^{3} }}} = {\displaystyle \frac{\displaystyle {\displaystyle D(\delta p)_{0} }}{\displaystyle {\displaystyle \nu }}}.$

(6.58)

Zdes' uchteno, chto v sootvetstvii s formuloi (5.21) $\ell _{z} = \alpha ^{ - 1}\sim \nu ^{ - 2},\; D$ - konstanta, harakterizuyushaya nelineinye i vyazkostnye svoistva sredy.

Nazad| Vpered

Publikacii s klyuchevymi slovami: kolebaniya - volny Publikacii so slovami: kolebaniya - volny
Sm. takzhe: Eho iz glubin krasnogo giganta

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce