Astronet > Kolebaniya i volny

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Kolebaniya i volny. Lekcii.

V.A.Aleshkevich, L.G.Dedenko, V.A.Karavaev (Fizicheskii fakul'tet MGU)
Izdatel'stvo Fizicheskogo fakul'teta MGU, 2001 g. Soderzhanie

V kachestve primera vypolnim nekotorye ocenki, illyustriruyushie kolichestvennye harakteristiki rasprostraneniya zvukovoi volny v vode, gde $D = 300 (Pa s)^{-1}.$ Pri chastote ul'trazvuka $\nu = 1 MGc$ rasstoyanie $\ell _{z} = 50 m,$ i uslovie ${\displaystyle \rm Re} \gt 10$ vypolnyaetsya, soglasno (6.58), dlya voln s amplitudoi zvukovogo davleniya $(\delta p)_{0} \gt 3 \cdot 10^{4}Pa,$ ili intensivnost'yu

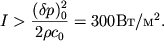$I \gt {\displaystyle \frac{\displaystyle {\displaystyle (\delta p)_{0}^{2} }}{\displaystyle {\displaystyle 2\rho c_{0} }}} = 300Vt/m^{2}.$

(6.59)

Sootvetstvuyushii uroven' zvukovogo davleniya $L_{p} \gt 180 dB.$ Dlya voln s takimi intensivnostyami $\ell _{nl} \lt \ell _{z} / 10 = 5 m,$ poetomu uzhe na pervyh metrah svoego rasprostraneniya ul'trazvukovaya volna budet prevrashat'sya v piloobraznuyu, i zatem pri $x \gt \ell _{nl}$ nachnetsya ee nelineinoe zatuhanie.

Kak pokazyvaet analiz formuly (6.54) s uchetom postroeniya polozheniya udarnogo fronta, izobrazhennogo na ris. 6.11, amplituda piloobraznoi volny pri ${\displaystyle \rm Re} \gg 1$ ubyvaet s proidennym rasstoyaniem $x$ po zakonu

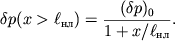$\delta p(x \gt \ell _{nl} ) = {\displaystyle \frac{\displaystyle {\displaystyle (\delta p)_{0} }}{\displaystyle {\displaystyle 1 + x / \ell _{nl} }}}.$

(6.60)

S pomosh'yu etoi formuly srazu mozhno sdelat' vazhnyi vyvod o tom, chto velichina $\delta p$ ne mozhet prevzoiti nekotoroe predel'noe znachenie, kak by my ni uvelichivali amplitudu garmonicheskoi volny $(\delta p)_{0}.$ Deistvitel'no, pri uvelichenii $(\delta p)_{0}$ velichina $\ell _{nl} \sim 1 / (\delta p)_{0}$ umen'shaetsya, i $\delta p$ stremitsya k $\delta p_{\max }.$ Velichina $\delta p_{\max }$ mozhet byt' korrektno podschitana pri odnovremennom uchete lineinogo poglosheniya i nelineinogo zatuhaniya (eto vyhodit za ramki nashego kursa) i okazyvaetsya ravnoi

$\delta p_{\max } = {\displaystyle \frac{\displaystyle {\displaystyle 4\nu }}{\displaystyle {\displaystyle D}}}e^{ - x / \ell _{z} }.$

(6.61)

Ocenim maksimal'noe znachenie intensivnosti $I_{max},$ kotoraya mozhet byt' peredana v vode ul'trazvukovym luchom s chastotoi $\nu = 1 MGc$ na rasstoyanie $x = 2\ell _{z} = 100 m$ :

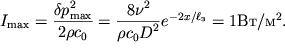$I_{\max } = {\displaystyle \frac{\displaystyle {\displaystyle \delta p_{\max }^{2} }}{\displaystyle {\displaystyle 2\rho c_{0} }}} = {\displaystyle \frac{\displaystyle {\displaystyle 8\nu ^{2}}}{\displaystyle {\displaystyle \rho c_{0} D^{2}}}}e^{ - 2x / \ell _{z} } = 1 Vt/m^{2}.$

(6.62)

Takim obrazom, v usloviyah, nailuchshih dlya vozbuzhdeniya moshnyh ul'trazvukovyh voln v vode, na rasstoyanie $x = 100 m$ cherez ploshad' secheniya 1 m² mozhno peredat' energiyu, dostatochnuyu lish' dlya svecheniya lampochki ot karmannogo fonarika. Eto ni v kakoe sravnenie ne idet s toi energiei, kotoruyu posylayut ul'trazvukovye pushki, ispol'zuemye geroyami nauchno-fantasticheskogo romana G. Adamova "Taina dvuh okeanov", gde ul'trazvukovym luchom yakoby povrezhdayut korabli i rakety.

V svyazi s vysheizlozhennym voznikaet estestvennyi vopros - a kak zhe ob'yasnit' razrushayushee deistvie vzryvnyh udarnyh voln na bol'shom rasstoyanii ot mesta vzryva? Otvet na etot vopros kroetsya v tom, chto vzryvnaya udarnaya volna predstavlyaet soboi odinochnyi impul's, i ego amplituda $\delta p$ ubyvaet s rasstoyaniem x bolee medlenno, chem u garmonicheskoi volny:

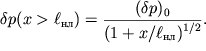$\delta p(x \gt \ell _{nl} ) = {\displaystyle \frac{\displaystyle {\displaystyle (\delta p)_{0} }}{\displaystyle {\displaystyle (1 + x / \ell _{nl} )^{1 / 2}}}}.$

(6.63)

Pri vozrastanii v epicentre vzryva amplitudy impul'sa $(\delta p)_{0}$ budet neogranichenno uvelichivat'sya i velichina $\delta p,$ kotoraya pri bol'shoi moshnosti zaryada okazhetsya dostatochnoi dlya razrusheniya prepyatstviya.

Nado otmetit', chto tem ne menee nelineinoe zatuhanie ne ogranichivaet shirokoe primenenie ul'trazvuka v laboratornyh usloviyah, poskol'ku $\ell _{nl}$ obychno sravnima s razmerami laboratornyh akusticheskih sistem ili prevoshodit ih.

Do sih por my govorili o rasprostranenii tol'ko odnoi volny. Odnako esli rasprostranyayutsya, naprimer, dve volny s chastotami $\omega _{1}$ i $\omega _{2},$ to nelineinoe vzaimodeistvie mezhdu nimi privodit k poyavleniyu voln s drugimi chastotami. Sredi nih volny s kratnymi chastotami $n_{1} \omega _{1}$ i $n_{2} \omega _{2}$ (garmoniki) i volny s kombinacionnymi chastotami $n_{1} \omega _{1} \pm n_{2} \omega _{2}$ ( $n_{1}$ i $n_{2}$ - celye chisla). V akustike, gde dispersiya otsutstvuet, vse eti volny dvizhutsya s odinakovoi skorost'yu, poetomu oni mogut effektivno vzaimodeistvovat' mezhdu soboi, prohodya bol'shie rasstoyaniya.

Generaciya garmonik i voln s kombinacionnymi chastotami imeet mnogochislennye primeneniya. Proillyustriruem skazannoe na dvuh primerah.

1. Pri izuchenii uprugih i prochnostnyh svoistv tverdyh materialov ih obychno podvergayut bol'shim nagruzkam s pomosh'yu special'nyh pressov, razvivayushih davleniya, blizkie k predelam prochnosti etih materialov ili prevoshodyashie ih, t.e. desyatki tysyach atmosfer. Vmesto etoi gromozdkoi i dorogostoyashei apparatury ispol'zuyut metody nelineinoi akustiki. Dlya etogo k odnomu torcu obrazca issleduemogo materiala prikleivayut p'ezoelektricheskii izluchatel' moshnoi akusticheskoi volny chastoty $\omega.$ Na drugom konce obrazca pomeshayut takoi zhe p'ezoelektricheskii preobrazovatel' (priemnik zvuka), na vyhode kotorogo registriruyut i zatem obrabatyvayut elektricheskii signal. Poslednii predstavlyaet soboi superpoziciyu kolebanii na chastotah $\omega, 2\omega, 3\omega$ i t.d. Govoryat, chto signal sostoit iz osnovnoi, vtoroi, tret'ei i t.d. garmonik. Signal na osnovnoi chastote neset informaciyu o lineinom module Yunga, tak kak soglasno zakonu Guka deformacii proporcional'ny prilozhennym napryazheniyam. V oblasti bol'shih napryazhenii vsledstvie plastichnosti i tekuchesti materiala svyaz' deformacii i napryazhenii opisyvayut s ispol'zovaniem nelineinyh modulei. Informaciyu o takih modulyah neset uzhe amplituda signala s chastotoi $2\omega$ (vtoraya garmonika), i t.d.

2. Drugim yarkim primerom ispol'zovaniya metodov nelineinoi akustiki yavlyaetsya generaciya v vode uzkonapravlennyh puchkov akusticheskih voln s dlinoi $\lambda .$ Eto osushestvlyaetsya s pomosh'yu tak nazyvaemyh parametricheskih antenn. Pri znakomstve s yavleniem difrakcii voln my otmechali, chto uglovaya rashodimost' $\vartheta$ zvukovogo puchka tem men'she, chem bol'she razmer $\ell$ peredayushego izluchatelya (antenny). Problemu izgotovleniya ogromnyh izluchayushih antenn s razmerami v desyatki metrov mozhno oboiti, ispol'zuya nelineinoe vzaimodeistvie v vode dvuh parallel'no rasprostranyayushihsya moshnyh zvukovyh voln s blizkimi chastotami $\omega _{1}$ i $\omega _{2}.$ Eti volny izluchayutsya gorizontal'no pogruzhennym v vodu odnim p'ezoizluchatelem razmerom $\ell \sim 10 sm.$ Obe volny do ih zatuhaniya proidut rasstoyanie $L\sim 10^{3} m.$ V etoi protyazhennoi oblasti rozhdaetsya volna nizkoi (raznostnoi) chastoty $\omega = \omega _{2} - \omega _{1},$ kotoraya zatuhaet gorazdo slabee i mozhet proiti ochen' bol'shie rasstoyaniya. Takim obrazom, vytyanutyi ob'em vody s malym poperechnym razmerom $\ell$ i bol'shim prodol'nym razmerom $L$ predstavlyaet soboi gigantskuyu estestvennuyu antennu, izluchayushuyu zvukovoi puchok raznostnoi chastoty vdol' samoi vytyanutoi antenny. Odnako, rashodimost' $\vartheta$ etogo puchka uzhe budet zadavat'sya vyrazheniem

$\vartheta = \lambda / L.$

(6.64)

Pri chastote $\nu = \omega / 2\pi \sim 1 kGc,\; \lambda \sim 1 m$ i pri $L\sim 10^{3} m$ poluchaem $\vartheta \sim 3\cdot 10^{ - 2} rad = 1,8^{ \circ }.$ Takaya chrezvychaino malaya rashodimost' puchka raznostnoi chastoty pozvolyaet s bol'shoi tochnost'yu provodit' morskie issledovaniya: izuchat' rel'ef dna, zanimat'sya arheologicheskimi izyskaniyami v pridonnyh sloyah grunta, v zailennyh ozerah, obnaruzhivat' skopleniya ryby u poverhnosti i dna morya, na melkovod'e - tam, gde obychnye gidrolokatory neeffektivny, i t.d.

Nazad| Vpered

Publikacii s klyuchevymi slovami: kolebaniya - volny Publikacii so slovami: kolebaniya - volny
Sm. takzhe: Eho iz glubin krasnogo giganta

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce