Astronet > Kolebaniya i volny

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Kolebaniya i volny. Lekcii.

V.A.Aleshkevich, L.G.Dedenko, V.A.Karavaev (Fizicheskii fakul'tet MGU)
Izdatel'stvo Fizicheskogo fakul'teta MGU, 2001 g. Soderzhanie

V 1834 godu shotlandskii inzhener-korablestroitel' i uchenyi Dzh. Rassel, nablyudaya za dvizheniem barzhi po kanalu, kotoruyu tashila para loshadei, obratil vnimanie na udivitel'noe yavlenie. Pri vnezapnoi ostanovke sudna massa vody vokrug barzhi v uzkom kanale ne ostanovilas', a sobralas' okolo nosa sudna, i zatem otorvalas' ot nego i v vide bol'shogo uedinennogo vodnogo holma stala dvigat'sya so skorost'yu okolo 8 mil' v chas. Udivitel'no, chto forma holma v processe ego dvizheniya prakticheski ne menyalas'. Rassel nazval eto dvizhusheesya po poverhnosti vody obrazovanie "great solitary wave", chto v perevode oznachaet "bol'shaya uedinennaya volna".

Teoreticheskoe ob'yasnenie uedinennye volny poluchili vposledstvii v rabotah francuzskogo uchenogo Zh. V. de Bussineska i angliiskogo fizika Dzh. Releya. Oni obosnovali matematicheski vozmozhnost' sushestvovaniya uedinennyh voln v melkovodnyh kanalah.

Posle smerti Rassela v 1895 godu gollandskii fizik D. Korteveg i ego uchenik G. de Fris vyveli uravnenie, opisyvayushee uedinennye volny. Eto uravnenie poluchilo nazvanie uravneniya Kortevega - de Frisa (uravnenie KDF) i imeet vid

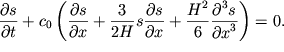${\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial t}}} + c_{0} \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial x}}} + {\displaystyle \frac{\displaystyle {\displaystyle 3}}{\displaystyle {\displaystyle 2H}}}s{\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial x}}} + {\displaystyle \frac{\displaystyle {\displaystyle H^{2}}}{\displaystyle {\displaystyle 6}}}{\displaystyle \frac{\displaystyle {\displaystyle \partial ^{3}s}}{\displaystyle {\displaystyle \partial x^{3}}}}} \right) = 0.$

(6.65)

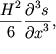Ono opisyvaet rasprostranenie poverhnostnyh gravitacionnyh voln na melkoi vode. Zdes' $c_{0} = \sqrt {\displaystyle gH}$ - skorost' voln melkoi vody, $H$ - glubina vodoema. Otmetim srazu, chto po vidu uravnenie KDF otlichaetsya ot nelineinogo uravneniya (6.50) nalichiem dopolnitel'nogo chlena ${\displaystyle \frac{\displaystyle {\displaystyle H^{2}}}{\displaystyle {\displaystyle 6}}}{\displaystyle \frac{\displaystyle {\displaystyle \partial ^{3}s}}{\displaystyle {\displaystyle \partial x^{3}}}},$ otvetstvennogo za dispersiyu gravitacionnyh voln (hotya i nebol'shuyu na melkoi vode).

Rassmotrim neskol'ko podrobnee vliyanie nelineinosti i dispersii na rasprostranenie poverhnostnyh gravitacionnyh voln. Po analogii s nelineinymi akusticheskimi volnami srazu mozhem skazat', chto skorost' razlichnyh uchastkov poverhnostnoi volny budet razlichna:

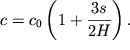$c = c_{0} \left( {\displaystyle 1 + {\displaystyle \frac{\displaystyle {\displaystyle 3s}}{\displaystyle {\displaystyle 2H}}}} \right).$

(6.66)

Iz-za razlichiya skorostei (greben' volny dvizhetsya bystree vpadiny) proishodit prevrashenie garmonicheskoi volny v piloobraznuyu. Krutoi front pod deistviem sily tyazhesti oprokidyvaetsya, i na poverhnosti vody poyavlyayutsya penistye grebeshki. Oprokidyvanie fronta legko nablyudat' pri dvizhenii volny po melkovod'yu vblizi berega (ris. 6.12). Odnako v ryade sluchaev nelineinoe iskazhenie volny mozhet kompensirovat'sya dispersiei. V samom dele, piloobraznaya volna predstavlyaet soboi nabor garmonicheskih voln s raznymi chastotami. Iz-za dispersii eti volny dvizhutsya s raznymi skorostyami, i poetomu piloobraznyi fragment volny, podobno impul'su, stremitsya rasshirit'sya. Pri opredelennoi forme fragmenta oba konkuriruyushih mehanizma mogut kompensirovat' drug druga, i togda po poverhnosti vody pobezhit ustoichivaya struktura v vide uedinennoi volny (solitona). Vyyasnim nekotorye svoistva etoi uedinennoi volny.

Ris. 6.12.

Predpolozhim, chto soliton imeet amplitudu $s_{0},$ protyazhennost' vdol' osi Ox, ravnuyu $\ell,$ i predstavlyaet soboi nekotoryi holmik, izobrazhennyi na risunke 6.13. Ocenim velichiny nelineinogo i dispersionnogo chlenov v uravnenii KDF:

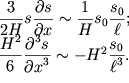$\begin{array}{l} {\displaystyle \frac{\displaystyle {\displaystyle 3}}{\displaystyle {\displaystyle 2H}}}s{\displaystyle \frac{\displaystyle {\displaystyle \partial s}}{\displaystyle {\displaystyle \partial x}}}\sim {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle H}}}s_{0} {\displaystyle \frac{\displaystyle {\displaystyle s_{0} }}{\displaystyle {\displaystyle \ell }}}; \\ {\displaystyle \frac{\displaystyle {\displaystyle H^{2}}}{\displaystyle {\displaystyle 6}}}{\displaystyle \frac{\displaystyle {\displaystyle \partial ^{3}s}}{\displaystyle {\displaystyle \partial x^{3}}}}\sim - H^{2}{\displaystyle \frac{\displaystyle {\displaystyle s_{0} }}{\displaystyle {\displaystyle \ell ^{3}}}}. \\ \end{array}$

(6.67)

V (6.67) uchteno, chto na perednem i zadnem frontah holmika 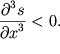${\displaystyle \frac{\displaystyle {\displaystyle \partial ^{3}s}}{\displaystyle {\displaystyle \partial x^{3}}}} \lt 0.$ Estestvenno, chto oba mehanizma budut kompensirovat' drug druga pri uslovii

${\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle H}}}s_{0} {\displaystyle \frac{\displaystyle {\displaystyle s_{0} }}{\displaystyle {\displaystyle \ell }}} - H^{2}{\displaystyle \frac{\displaystyle {\displaystyle s_{0} }}{\displaystyle {\displaystyle \ell ^{3}}}} \approx 0.$

(6.68)

Poslednee nakladyvaet svyaz' na amplitudu $s_{0}$ i dlinu $\ell$ solitona:

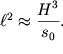$\ell ^{2} \approx {\displaystyle \frac{\displaystyle {\displaystyle H^{3}}}{\displaystyle {\displaystyle s_{0} }}}.$

(6.69)

Takim obrazom, chem bol'she amplituda solitona $s_{0},$ tem men'she dolzhna byt' ego dlina $\ell.$ Skorost' solitona c vozrastaet s rostom amplitudy, chto harakterno dlya nelineinogo rasprostraneniya voln.

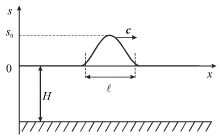Ris. 6.13.

Tochnoe reshenie uravneniya KDF, opisyvayushee soliton, imeet vid

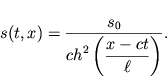$s(t,x) = {\displaystyle \frac{\displaystyle {\displaystyle s_{0} }}{\displaystyle {\displaystyle ch^{2}\left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle x - ct}}{\displaystyle {\displaystyle \ell }}}} \right)}}}.$

(6.70)

Pri etom dlina solitona $\ell$ svyazana s amplitudoi $s_{0}$ sootnosheniem

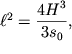$\ell ^{2} = {\displaystyle \frac{\displaystyle {\displaystyle 4H^{3}}}{\displaystyle {\displaystyle 3s_{0} }}},$

(6.71)

a skorost'

$c = c_{0} \left( {\displaystyle 1 + {\displaystyle \frac{\displaystyle {\displaystyle s_{0} }}{\displaystyle {\displaystyle 2H}}}} \right).$

(6.72)

Esli $s_{0} \ll H,$ to poslednee vyrazhenie mozhno perepisat' v vide

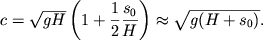$c = \sqrt {\displaystyle gH} \left( {\displaystyle 1 + {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}{\displaystyle \frac{\displaystyle {\displaystyle s_{0} }}{\displaystyle {\displaystyle H}}}} \right) \approx \sqrt {\displaystyle g(H + s_{0} )}.$

(6.73)

Etu formulu my uzhe zapisyvali pri kachestvennom obsuzhdenii povedeniya gravitacionnyh voln po mere ih priblizheniya k beregu.

Vazhno podcherknut', chto soliton yavlyaetsya ustoichivoi strukturoi. Esli pervonachal'no sootnoshenie (6.71) ne vypolnyaetsya i amplituda $s_{0}$ slishkom velika, to vodyanoi holm raspadaetsya na neskol'ko men'shih holmikov, iz kotoryh sformiruyutsya solitony. Naprotiv, esli $s_{0}$ slishkom mala, to takoi nizkii holm raspolzetsya vsledstvie dispersii.

Po sovremennym predstavleniyam bol'shinstvo voln cunami obrazuyutsya, kogda dostatochno krupnyi, no bezvrednyi v okeane soliton vybrasyvaetsya na bereg. Pri podhode k beregu on stanovitsya vyshe i koroche, i ego vysota stanovitsya sravnima s glubinoi okeana vblizi berega.

V zaklyuchenie etoi temy otmetim, chto v nastoyashee vremya obnaruzheny solitony dlya voln razlichnoi prirody. Tak, naprimer, sushestvuyut solitony pri rasprostranenii akusticheskih voln v kristallah, svetovyh impul'sov v volokonnyh svetovodah, ionno-zvukovyh voln v plazme i dr. Vo vseh sluchayah sushestvovanie solitonov obuslovleno vzaimnoi kompensaciei nelineinyh i dispersionnyh effektov. Estestvenno, chto energiya, perenosimaya uedinennoi volnoi lyuboi prirody, budet dissipirovat' v teplo, poetomu po mere rasprostraneniya amplituda solitona budet stremit'sya umen'shit'sya, chto, estestvenno, rano ili pozdno privedet k ego ischeznoveniyu.

Nazad

Publikacii s klyuchevymi slovami: kolebaniya - volny Publikacii so slovami: kolebaniya - volny
Sm. takzhe: Eho iz glubin krasnogo giganta

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

Kolebaniya i volny. Lekcii.

Uedinennye volny (solitony).