Astronet > Kolebaniya i volny

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Kolebaniya i volny. Lekcii.

V.A.Aleshkevich, L.G.Dedenko, V.A.Karavaev (Fizicheskii fakul'tet MGU)
Izdatel'stvo Fizicheskogo fakul'teta MGU, 2001 g. Soderzhanie

Fazovyi portret kolebatel'noi sistemy.

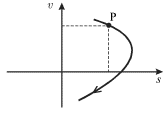
V lyuboi kolebatel'noi sisteme s odnoi stepen'yu svobody smeshenie $s(t)$ i skorost' $v(t) = ds / dt$ menyayutsya so vremenem. Sostoyanie sistemy v kazhdyi moment vremeni mozhno harakterizovat' dvumya znacheniyami $s$ i $v,$ i na ploskosti etih peremennyh eto sostoyanie odnoznachno opredelyaetsya polozheniem izobrazhayushei tochki P s koordinatami $s$ i $v$ . S techeniem vremeni izobrazhayushaya tochka P budet peremeshat'sya po krivoi, kotoruyu nazyvayut fazovoi traektoriei dvizheniya (ris. 1.10).

Ris. 1.10.

Ploskost' peremennyh $s$ i $v$ nazyvaetsya fazovoi ploskost'yu. Semeistvo fazovyh traektorii obrazuet fazovyi portret kolebatel'noi sistemy. Analiz fazovogo portreta daet hotya i ne polnuyu, no obshirnuyu informaciyu o kolebatel'noi sisteme. K postroeniyu takogo portreta pribegayut togda, kogda ne udaetsya reshit' analiticheski uravnenie, opisyvayushee slozhnye kolebaniya. V pervuyu ochered' eto otnositsya k nelineinym kolebaniyam, analiz kotoryh zatrudnen iz-za otsutstviya tochnyh reshenii nelineinyh uravnenii.

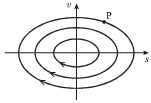
Vnachale proillyustriruem skazannoe na primere prosteishih garmonicheskih kolebanii vida $s(t) = s_{0} \sin (\omega _{0} t + \varphi _{0} ).$ Poskol'ku skorost' $v(t) = {\displaystyle \frac{\displaystyle {\displaystyle ds}}{\displaystyle {\displaystyle dt}}} = s_{0} \omega _{0} \sin \left( {\displaystyle \omega _{0} t + \varphi _{0} + {\displaystyle \frac{\displaystyle {\displaystyle \pi }}{\displaystyle {\displaystyle 2}}}} \right)$ operezhaet smeshenie po faze na $\pi / 2,$ to fazovaya traektoriya budet ellipsom. Tochka P budet dvigat'sya po ellipticheskoi traektorii po chasovoi strelke (pri $v \gt 0$ smeshenie $s$ uvelichivaetsya, a pri $v \lt 0$ - umen'shaetsya (ris. 1.11)).

Ris. 1.11.

Parametry ellipsa opredelyayutsya energiei, zapasennoi garmonicheskim oscillyatorom. Potencial'naya energiya pruzhinnogo mayatnika proporcional'na kvadratu smesheniya:

$E_{pot} = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}ks^{2} = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}ks_{0}^{2} \sin ^{2}(\omega _{0} t + \varphi _{0} ).$

(1.24)

Kineticheskaya energiya proporcional'na kvadratu skorosti:

$E_{kin} = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}mv^{2} = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}m\omega _{0}^{2} s_{0}^{2} \cos ^{2}(\omega _{0} t + \varphi _{0} ).$

(1.25)

Esli prinyat' vo vnimanie ravenstvo $k = m\omega _{0}^{2},$ to legko videt', chto vzaimoprevrasheniya odnogo vida energii v drugoi za period proishodyat dvazhdy. Pri etom polnaya energiya sistemy ostaetsya postoyannoi:

$E_{0} = E_{pot} + E_{kin} = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}m(\omega _{0}^{2} s^{2} + v^{2}).$

(1.26)

Ravenstvo (1.26) kak raz i yavlyaetsya uravneniem ellipsa, kotoroe mozhno perepisat' v bolee udobnom vide:

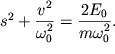$s^{2} + {\displaystyle \frac{\displaystyle {\displaystyle v^{2}}}{\displaystyle {\displaystyle \omega _{0}^{2} }}} = {\displaystyle \frac{\displaystyle {\displaystyle 2E_{0} }}{\displaystyle {\displaystyle m\omega _{0}^{2} }}}.$

(1.27)

Fazovyi portret garmonicheskogo oscillyatora predstavlyaet soboi semeistvo ellipsov, kazhdomu iz kotoryh sootvetstvuet energiya $E_{0},$ zapasennaya oscillyatorom. Polozhenie ravnovesiya v tochke 0 na fazovoi ploskosti yavlyaetsya osoboi tochkoi i nazyvaetsya osoboi tochkoi tipa "centr".

S uvelicheniem energii $E_{0}$ vozrastayut amplitudy kolebanii smesheniya $s_{0}$ i skorosti $s_{0} \omega _{0} .$ Kolebaniya, kak pravilo, perestayut byt' garmonicheskimi, a fazovye traektorii - ellipsami.

Ris. 1.12.

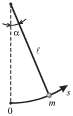
Proanaliziruem na fazovoi ploskosti kolebaniya matematicheskogo mayatnika pri proizvol'nyh uglah $\alpha$ otkloneniya ot polozheniya ravnovesiya. Pri etom budem schitat', chto tochechnaya massa $m$ prikreplena ne k niti, a k zhestkomu nevesomomu sterzhnyu dliny $\ell .$ Pervoe iz uravnenii (1.2) zapishem v vide

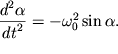${\displaystyle \frac{\displaystyle {\displaystyle d^{2}\alpha }}{\displaystyle {\displaystyle dt^{2}}}} = - \omega _{0}^{2} \sin \alpha .$

(1.28)

Eto nelineinoe uravnenie ne imeet tochnogo analiticheskogo resheniya, poetomu pozdnee my privedem ego priblizhennoe reshenie. Odnako mnogie zakonomernosti takih kolebanii mozhno proanalizirovat' s ispol'zovaniem fazovogo portreta na ploskosti $(\alpha ; \dot {\displaystyle \alpha } = {\displaystyle \frac{\displaystyle {\displaystyle d\alpha }}{\displaystyle {\displaystyle dt}}}).$ S etoi cel'yu uravnenie (1.28) nado preobrazovat' k takomu vidu, chtoby v nem ostalis' tol'ko eti peremennye, a vremya bylo by isklyucheno. Dlya etogo uglovoe uskorenie v levoi chasti (1.28) preobrazuem k vidu:

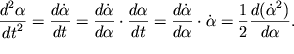${\displaystyle \frac{\displaystyle {\displaystyle d^{2}\alpha }}{\displaystyle {\displaystyle dt^{2}}}} = {\displaystyle \frac{\displaystyle {\displaystyle d\dot {\displaystyle \alpha }}}{\displaystyle {\displaystyle dt}}} = {\displaystyle \frac{\displaystyle {\displaystyle d\dot {\displaystyle \alpha }}}{\displaystyle {\displaystyle d\alpha }}} \cdot {\displaystyle \frac{\displaystyle {\displaystyle d\alpha }}{\displaystyle {\displaystyle dt}}} = {\displaystyle \frac{\displaystyle {\displaystyle d\dot {\displaystyle \alpha }}}{\displaystyle {\displaystyle d\alpha }}} \cdot \dot {\displaystyle \alpha } = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}{\displaystyle \frac{\displaystyle {\displaystyle d(\dot {\displaystyle \alpha }^{2})}}{\displaystyle {\displaystyle d\alpha }}}.$

(1.29)

Podstavlyaya (1.29) v (1.28), poluchim

${\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}d(\dot {\displaystyle \alpha }^{2}) = - \omega _{0}^{2} \sin \alpha d\alpha .$

(1.30)

Uravnenie (1.30) otrazhaet tot fakt, chto prirashenie kineticheskoi energii mayatnika ravno ubyli ego potencial'noi energii v pole sily tyazhesti. Integriruya (1.30), poluchim

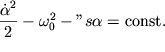$$ {\displaystyle \frac{\displaystyle {\displaystyle \dot {\displaystyle \alpha }^{2}}}{\displaystyle {\displaystyle 2}}} - \omega _{0}^{2} -$

(1.31)

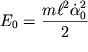Esli prinyat', chto potencial'naya energiya mayatnika v polozhenii ravnovesiya ravna nulyu, to konstanta vyrazhaetsya cherez zapasennuyu mayatnikom energiyu $E_{0} = {\displaystyle \frac{\displaystyle {\displaystyle m\ell ^{2}\dot {\displaystyle \alpha }_{0}^{2} }}{\displaystyle {\displaystyle 2}}}$ ( $\dot {\displaystyle \alpha }_{0}$ - uglovaya skorost' mayatnika v polozhenii ravnovesiya):

${\displaystyle \rm const}\; = {\displaystyle \frac{\displaystyle {\displaystyle E_{0} }}{\displaystyle {\displaystyle m\ell ^{2}}}} - \omega _{0}^{2} .$

(1.32)

Uravnenie fazovoi traektorii (1.31) okonchatel'no zapishetsya v vide:

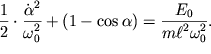${\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}} \cdot {\displaystyle \frac{\displaystyle {\displaystyle \dot {\displaystyle \alpha }^{2}}}{\displaystyle {\displaystyle \omega _{0}^{2} }}} + \left( {\displaystyle 1 - \cos \alpha } \right) = {\displaystyle \frac{\displaystyle {\displaystyle E_{0} }}{\displaystyle {\displaystyle m\ell ^{2}\omega _{0}^{2} }}}.$

(1.33)

Pri etom potencial'naya i kineticheskaya energii zadayutsya vyrazheniyami

$E_{kin} = {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 2}}}m\ell ^{2}\dot {\displaystyle \alpha }^{2}; \quad E_{kin} = m\ell ^{2}\omega _{0}^{2} \left( {\displaystyle 1 - \cos \alpha } \right).$

(1.34)

Ispol'zuya (1.33), postroim fazovyi portret sistemy (ris. 1.13).

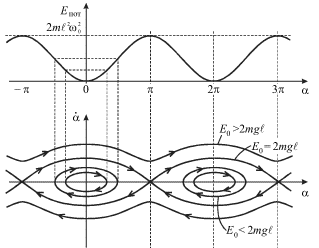Ris. 1.13.

Otchetlivo vidny dva tipa fazovyh traektorii, sootvetstvuyushie dvum tipam dvizheniya. Zamknutye traektorii, okruzhayushie osobye tochki tipa "centr" s koordinatami $\dot {\displaystyle \alpha } = 0, \alpha = 2\pi n$ ( $n$ - celoe chislo), sootvetstvuyut kolebaniyam mayatnika otnositel'no ustoichivogo nizhnego polozheniya ravnovesiya. Takie kolebaniya imeyut mesto, esli energiya sistemy $E_{0} \lt m\ell ^{2}\omega _{0}^{2} = 2mg\ell$ (sm. ris. 1.13). Pri etom, esli $E_{0} \ll 2mg\ell,$ to kolebaniya budut garmonicheskimi, a fazovye traektorii - ellipsami. Esli $E_{0} \sim mg\ell,$ to kolebaniya budut negarmonicheskimi. Pri uvelichenii energii, a, znachit, i amplitudy kolebanii oscillyatora, ih period budet vozrastat', poskol'ku vozvrashayushaya sila v uravnenii (1.28) men'she, chem v sluchae garmonicheskogo oscillyatora.

Verhnemu polozheniyu ravnovesiya s koordinatami $\dot {\displaystyle \alpha } = 0, \alpha = \left( {\displaystyle 2n - 1} \right)\pi$ sootvetstvuyut osobye tochki tipa "sedlo". Fazovye krivye, prohodyashie cherez "sedla", sootvetstvuyut energii $E_{0} = 2mg\ell$ i nazyvayutsya separatrisami.

Esli, nakonec, $E_{0} \gt 2mg\ell,$ to poluchayutsya nezamknutye (ubegayushie) traektorii, sootvetstvuyushie vrashatel'nomu dvizheniyu mayatnika.

Takim obrazom, separatrisy razdelyayut fazovuyu ploskost' na dve oblasti: oblast' zamknutyh traektorii i oblast' traektorii, prihodyashih iz beskonechnosti i uhodyashih v beskonechnost'.

Otmetim, chto dlya negarmonicheskih kolebanii nel'zya upotreblyat' termin "krugovaya chastota", poskol'ku, kak budet pokazano nizhe, takie kolebaniya yavlyayutsya, kak pravilo, superpoziciei garmonicheskih kolebanii s razlichnymi chastotami. Period zhe yavlyaetsya po-prezhnemu odnoi iz glavnyh harakteristik kolebanii. Fazovyi portret ne pozvolyaet opredelit', kak bystro dvizhetsya tochka R po traektorii. Odnako period nelineinyh kolebanii matematicheskogo mayatnika mozhno poluchit' na osnove priblizhennogo resheniya uravneniya (1.28).

Nazad| Vpered

Publikacii s klyuchevymi slovami: kolebaniya - volny Publikacii so slovami: kolebaniya - volny
Sm. takzhe: Eho iz glubin krasnogo giganta

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce