Astronet > Kolebaniya i volny

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Kolebaniya i volny. Lekcii.

V.A.Aleshkevich, L.G.Dedenko, V.A.Karavaev (Fizicheskii fakul'tet MGU)
Izdatel'stvo Fizicheskogo fakul'teta MGU, 2001 g. Soderzhanie

Negarmonicheskie kolebaniya matematicheskogo mayatnika.

Kolebaniya matematicheskogo mayatnika pri bol'shih amplitudah, kak uzhe otmechalos', ne budut garmonicheskimi. Eto proishodit potomu, chto vozvrashayushaya sila v pravoi chasti uravneniya (1.28) proporcional'na $\sin \alpha$ i pri bol'shih $\alpha$ stanovitsya men'she toi "lineinoi" sily (proporcional'noi $\alpha$ ), kotoraya vozvrashaet koleblyushuyusya massu v polozhenie ravnovesiya za neizmennoe vremya, ravnoe chetverti perioda kolebanii. Takaya "lineinaya" sila obespechivaet nezavisimost' etogo vremeni ot amplitudy $\alpha _{0},$ t.e. izohronnost' kolebanii.

Dlya analiza kolebanii pri bol'shih amplitudah $\alpha _{0}$ zapishem razlozhenie $\sin \alpha$ v ryad:

$\sin \alpha = \alpha - {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 6}}}\alpha ^{3} + \ldots \quad,$

(1.35)

v kotorom otbrosheny chleny bolee vysokogo poryadka: $\alpha ^{5}, \alpha ^{7}$ i t.d. Podstanovka (1.35) v (1.28) privodit k nelineinomu uravneniyu kolebanii:

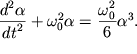${\displaystyle \frac{\displaystyle {\displaystyle d^{2}\alpha }}{\displaystyle {\displaystyle dt^{2}}}} + \omega _{0}^{2} \alpha = {\displaystyle \frac{\displaystyle {\displaystyle \omega _{0}^{2} }}{\displaystyle {\displaystyle 6}}}\alpha ^{3}.$

(1.36)

Resheniem etogo uravneniya uzhe ne budet garmonicheskaya funkciya. Deistvitel'no, dopustim, chto resheniem uravneniya (1.36) budet garmonicheskoe kolebanie vida $\alpha (t) = \alpha _{0} \sin (\omega t + \varphi _{0} ).$ Podstavlyaya eto vyrazhenie v pravuyu chast' (1.36) i uchityvaya trigonometricheskoe tozhdestvo

$\sin ^{3}\omega t \equiv {\displaystyle \frac{\displaystyle {\displaystyle 3}}{\displaystyle {\displaystyle 4}}}\sin \omega t - {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 4}}}\sin 3\omega t,$

(1.37)

prihodim k protivorechiyu. Poluchaetsya tak, chto nelineinyi chlen v pravoi chasti uravneniya izmenyaetsya vo vremeni ne tol'ko s osnovnoi chastotoi $\omega,$ no takzhe i s utroennoi chastotoi $3\omega$ (chastotoi tret'ei garmoniki). Chtoby ustranit' eto protivorechie, budem schitat', chto kolebaniya mayatnika proishodyat odnovremenno na chastotah $\omega$ i $3\omega$ tak, chto

$\alpha (t) = \alpha _{0} \sin (\omega t + \varphi _{0} ) + \varepsilon \alpha _{0} \sin 3(\omega t + \varphi _{0} ),$

(1.38)

gde $\varepsilon$ - bezrazmernyi parametr.

Podstavlyaya (1.38) v (1.36), snova obnaruzhivaem, chto nelineinyi chlen, pomimo dvuh chastot $\omega$ i $3\omega,$ menyaetsya vo vremeni i na chastote $9\omega .$ Eto govorit o tom, chto reshenie (1.38) ne yavlyaetsya polnym (v nem otsutstvuyut vysshie garmoniki $9\omega, 27\omega$ i t.d.). Mezhdu tem, esli amplituda kolebanii $\alpha _{0}$ ne ochen' velika, to parametr $\varepsilon \ll 1,$ i otsutstvuyushie chleny s vysshimi garmonikami imeyut amplitudy $\varepsilon ^{2}\alpha _{0}, \varepsilon ^{3}\alpha _{0}$ i t. d., kotorye mnogo men'she amplitudy tret'ei garmoniki $\varepsilon \alpha _{0} .$

Teper' rasschitaem chastotu $\omega .$ Dlya prostoty polozhim $\varphi _{0} = 0$ (mayatnik poluchaet nachal'nyi tolchok v polozhenii ravnovesiya). Ispol'zuya (1.38), zapishem kazhdyi iz treh chlenov uravneniya (1.36), opuskaya slagaemye, imeyushie poryadok malosti $\varepsilon ^{2}$ i vyshe:

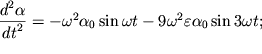${\displaystyle \frac{\displaystyle {\displaystyle d^{2}\alpha }}{\displaystyle {\displaystyle dt^{2}}}} = - \omega ^{2}\alpha _{0} \sin \omega t - 9\omega ^{2}\varepsilon \alpha _{0} \sin 3\omega t;$	(1.39)
$\omega _{0}^{2} \alpha = \omega _{0}^{2} \alpha _{0} \sin \omega t + \omega _{0}^{2} \varepsilon \alpha _{0} \sin 3\omega t;$
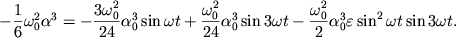$- {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 6}}}\omega _{0}^{2} \alpha ^{3} = - {\displaystyle \frac{\displaystyle {\displaystyle 3\omega _{0}^{2} }}{\displaystyle {\displaystyle 24}}}\alpha _{0}^{3} \sin \omega t + {\displaystyle \frac{\displaystyle {\displaystyle \omega _{0}^{2} }}{\displaystyle {\displaystyle 24}}}\alpha _{0}^{3} \sin 3\omega t - {\displaystyle \frac{\displaystyle {\displaystyle \omega _{0}^{2} }}{\displaystyle {\displaystyle 2}}}\alpha _{0}^{3} \varepsilon \sin ^{2}\omega t\sin 3\omega t.$

Zametim, chto v poslednem ravenstve tret'e slagaemoe v pravoi chasti, soderzhashee mnozhitel' $\alpha _{0}^{3} \varepsilon,$ malo po sravneniyu s dvumya predydushimi, i ego takzhe mozhno otbrosit'.

Slozhim poluchennye tri ravenstva. V silu (1.36), summa levyh chastei ravenstv (1.39) ravna nulyu. Poetomu

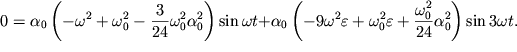$0 = \alpha _{0} \left( {\displaystyle - \omega ^{2} + \omega _{0}^{2} - {\displaystyle \frac{\displaystyle {\displaystyle 3}}{\displaystyle {\displaystyle 24}}}\omega _{0}^{2} \alpha _{0}^{2} } \right)\sin \omega t + \alpha _{0} \left( {\displaystyle - 9\omega ^{2}\varepsilon + \omega _{0}^{2} \varepsilon + {\displaystyle \frac{\displaystyle {\displaystyle \omega _{0}^{2} }}{\displaystyle {\displaystyle 24}}}\alpha _{0}^{2} } \right)\sin 3\omega t.$

(1.40)

Poskol'ku ravenstvo (1.40) dolzhno vypolnyat'sya dlya lyubogo momenta vremeni, to kazhdoe iz vyrazhenii, stoyashih v kruglyh skobkah, dolzhno ravnyat'sya nulyu. Iz ravenstva nulyu pervogo vyrazheniya legko opredelit' kvadrat chastoty osnovnoi garmoniki

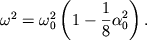$\omega ^{2} = \omega _{0}^{2} \left( {\displaystyle 1 - {\displaystyle \frac{\displaystyle {\displaystyle 1}}{\displaystyle {\displaystyle 8}}}\alpha _{0}^{2} } \right).$

(1.41)

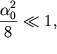Esli ${\displaystyle \frac{\displaystyle {\displaystyle \alpha _{0}^{2} }}{\displaystyle {\displaystyle 8}}} \ll 1,$ to dlya chastoty poluchim

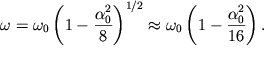$\omega = \omega _{0} \left( {\displaystyle 1 - {\displaystyle \frac{\displaystyle {\displaystyle \alpha _{0}^{2} }}{\displaystyle {\displaystyle 8}}}} \right)^{1 / 2} \approx \omega _{0} \left( {\displaystyle 1 - {\displaystyle \frac{\displaystyle {\displaystyle \alpha _{0}^{2} }}{\displaystyle {\displaystyle 16}}}} \right).$

(1.42)

Poslednee vyrazhenie pokazyvaet, chto s vozrastaniem amplitudy kolebanii ih chastota umen'shaetsya (period uvelichivaetsya), t.e. narushaetsya izohronnost' kolebanii.

Priravnyaem dalee nulyu vtoroe vyrazhenie v kruglyh skobkah v formule (1.40):

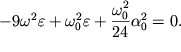$- 9\omega ^{2}\varepsilon + \omega _{0}^{2} \varepsilon + {\displaystyle \frac{\displaystyle {\displaystyle \omega _{0}^{2} }}{\displaystyle {\displaystyle 24}}}\alpha _{0}^{2} = 0.$

(1.43)

Schitaya, chto $\omega \approx \omega _{0},$ nahodim velichinu malogo koefficienta $\varepsilon$ :

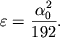$\varepsilon = {\displaystyle \frac{\displaystyle {\displaystyle \alpha _{0}^{2} }}{\displaystyle {\displaystyle 192}}}.$

(1.44)

Esli polozhit' $\alpha _{0} = 15^{\circ} = 0,26 rad,$ to $\varepsilon = 3,5 \cdot 10^{ - 4},$ i vklad tret'ei garmoniki v kolebaniya nichtozhno mal. Otlichie chastoty \omega ot chastoty garmonicheskih kolebanii $\omega _{0}$ sostavit velichinu

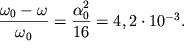${\displaystyle \frac{\displaystyle {\displaystyle \omega _{0} - \omega }}{\displaystyle {\displaystyle \omega _{0} }}} = {\displaystyle \frac{\displaystyle {\displaystyle \alpha _{0}^{2} }}{\displaystyle {\displaystyle 16}}} = 4,2 \cdot 10^{ - 3}.$

(1.45)

Dazhe pri $\alpha _{0} \sim 1 rad \; \varepsilon \approx 5 \cdot 10^{ - 3},$ a ${\displaystyle \frac{\displaystyle {\displaystyle \omega _{0} - \omega }}{\displaystyle {\displaystyle \omega _{0} }}}\sim 6\% .$ Takim obrazom, priblizhennym resheniem uravneniya (1.36) budet (1.38), gde chastota $\omega$ opredelyaetsya (1.41), a parametr $\varepsilon$ nahoditsya iz (1.44).

Zametim, chto negarmonicheskie kolebaniya mogut voznikat' ne tol'ko pri bol'shih otkloneniyah ot polozheniya ravnovesiya sistemy. Naprimer, esli v razlozhenii vozvrashayushei sily $F_{\tau } (s)$ po stepenyam $s$ otsutstvuet lineinyi chlen, i ono nachinaetsya s chlena, proporcional'nogo $s^{3},$ to kolebaniya budut angarmonicheskimi pri lyubyh, dazhe skol' ugodno malyh otkloneniyah.

Nazad| Vpered

Publikacii s klyuchevymi slovami: kolebaniya - volny Publikacii so slovami: kolebaniya - volny
Sm. takzhe: Eho iz glubin krasnogo giganta

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce