Kolebaniya i volny. Lekcii.
V.A.Aleshkevich, L.G.Dedenko, V.A.Karavaev (Fizicheskii fakul'tet MGU)Izdatel'stvo Fizicheskogo fakul'teta MGU, 2001 g. Soderzhanie
Svobodnye kolebaniya v dissipativnyh sistemah s vyazkim treniem.
V real'nyh sistemah vsegda proishodit dissipaciya energii. Esli poteri energii ne budut kompensirovat'sya za schet vneshnih ustroistv, to kolebaniya s techeniem vremeni budut zatuhat' i cherez kakoe-to vremya prekratyatsya voobshe.
Formal'no zatuhayushie kolebaniya opisyvayutsya uravneniem
| (1.46) |
kotoroe, v otlichie ot (1.2), pomimo vozvrashayushei sily ![]() soderzhit
i silu treniya
soderzhit
i silu treniya ![]() Sila soprotivleniya dvizheniyu, voobshe govorya, zavisit
kak ot napravleniya skorosti (naprimer, pri suhom trenii), tak i ot velichiny
skorosti (pri dvizhenii v vyazkoi srede). Esli vozvrashayushaya sila
proporcional'na smesheniyu:
Sila soprotivleniya dvizheniyu, voobshe govorya, zavisit
kak ot napravleniya skorosti (naprimer, pri suhom trenii), tak i ot velichiny
skorosti (pri dvizhenii v vyazkoi srede). Esli vozvrashayushaya sila
proporcional'na smesheniyu: ![]() gde
gde ![]() - koefficient
proporcional'nosti (dlya pruzhinnogo mayatnika - zhestkost' pruzhiny), to
uravnenie (1.46) mozhno perepisat' v vide
- koefficient
proporcional'nosti (dlya pruzhinnogo mayatnika - zhestkost' pruzhiny), to
uravnenie (1.46) mozhno perepisat' v vide
| (1.47) |
gde 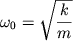 - sobstvennaya chastota
nezatuhayushih garmonicheskih kolebanii.
- sobstvennaya chastota
nezatuhayushih garmonicheskih kolebanii.
Vnachale my rassmotrim zatuhayushie kolebaniya v sluchae, kogda na koleblyusheesya
telo deistvuet sila vyazkogo treniya, proporcional'naya skorosti: ![]() Takaya situaciya mozhet imet' mesto, naprimer, pri
kolebatel'nom dvizhenii tela v vozduhe ili zhidkosti, kogda chislo Reinol'dsa
Takaya situaciya mozhet imet' mesto, naprimer, pri
kolebatel'nom dvizhenii tela v vozduhe ili zhidkosti, kogda chislo Reinol'dsa
![]() ili
ili ![]() . Togda uravnenie (1.47) mozhno zapisat' v vide:
. Togda uravnenie (1.47) mozhno zapisat' v vide:
| (1.48) |
gde ![]() - koefficient, ili pokazatel' zatuhaniya.
- koefficient, ili pokazatel' zatuhaniya.
Obshaya ideya resheniya odnorodnyh lineinyh uravnenii tipa (1.48) zaklyuchaetsya v
sleduyushem: v kachestve funkcional'noi zavisimosti ![]() nado vybrat' takuyu,
kotoraya pri differencirovanii po vremeni perehodit v samu sebya, to est'
eksponentu:
nado vybrat' takuyu,
kotoraya pri differencirovanii po vremeni perehodit v samu sebya, to est'
eksponentu: ![]() Podstavim ee v uravnenie (1.48):
Podstavim ee v uravnenie (1.48):
| (1.49) |
Poskol'ku ![]() poluchaem tak nazyvaemoe
"harakteristicheskoe" uravnenie:
poluchaem tak nazyvaemoe
"harakteristicheskoe" uravnenie:
| (1.50) |
kotoroe v dannom sluchae (dlya uravneniya vtorogo poryadka) imeet dva kornya
| (1.51) |
a samo uravnenie (1.48) - dva nezavisimyh resheniya: ![]() i
i ![]() V silu
lineinosti uravneniya (1.48) summa lyubyh ego reshenii takzhe yavlyaetsya resheniem,
to est' spravedliv tak nazyvaemyi "princip superpozicii" reshenii, i obshim
resheniem dannogo uravneniya yavlyaetsya
V silu
lineinosti uravneniya (1.48) summa lyubyh ego reshenii takzhe yavlyaetsya resheniem,
to est' spravedliv tak nazyvaemyi "princip superpozicii" reshenii, i obshim
resheniem dannogo uravneniya yavlyaetsya
| (1.52) |
Reshenie soderzhit dve nezavisimye konstanty ![]() i
i ![]() kotorye
opredelyayutsya iz nachal'nyh uslovii
kotorye
opredelyayutsya iz nachal'nyh uslovii ![]()
V zavisimosti ot sootnosheniya ![]() i
i ![]() vozmozhny tri sluchaya.
vozmozhny tri sluchaya.
Esli ![]() to
to ![]() gde
gde ![]() -
"mnimaya" edinica. Reshenie yavlyaetsya kompleksnym1, no, poskol'ku nachal'nye usloviya
deistvitel'nye, to s pomosh'yu formuly Eilera:
-
"mnimaya" edinica. Reshenie yavlyaetsya kompleksnym1, no, poskol'ku nachal'nye usloviya
deistvitel'nye, to s pomosh'yu formuly Eilera:
| (1.53) |
netrudno pokazat', chto obshee reshenie budet deistvitel'no i mozhet byt' zapisano v vide:
| (1.54) |
to est' predstavlyaet soboi zatuhayushie kolebaniya, chastota kotoryh ![]() men'she, chem u sobstvennyh nezatuhayushih kolebanii:
men'she, chem u sobstvennyh nezatuhayushih kolebanii:
| (1.55) |
Kolebaniya, opisyvaemye (1.54), ne yavlyayutsya garmonicheskimi (ris. 1.14). Pod ih amplitudoi budem ponimat' velichinu
| (1.56) |
kotoraya monotonno ubyvaet so vremenem. "Dlitel'nost'" kolebanii harakterizuetsya vremenem zatuhaniya
| (1.57) |
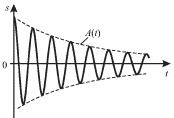 |
| Ris. 1.14. |
Esli podstavit' ![]() v (1.56), to legko videt', chto po istechenii vremeni
zatuhaniya
v (1.56), to legko videt', chto po istechenii vremeni
zatuhaniya ![]() amplituda ubyvaet v e raz. Kolichestvo sovershennyh sistemoi
kolebanii za vremya
amplituda ubyvaet v e raz. Kolichestvo sovershennyh sistemoi
kolebanii za vremya ![]() ravno otnosheniyu etogo vremeni k periodu
zatuhayushih kolebanii
ravno otnosheniyu etogo vremeni k periodu
zatuhayushih kolebanii ![]() Esli zatuhanie v sisteme malo
Esli zatuhanie v sisteme malo
![]() to period kolebanii
to period kolebanii ![]() i chislo etih kolebanii veliko:
i chislo etih kolebanii veliko:
| (1.58) |
Eksponencial'nyi zakon ubyvaniya amplitudy so vremenem pozvolyaet vvesti
bezrazmernyi parametr - logarifmicheskii dekrement zatuhaniya ![]() kotoryi raven logarifmu otnosheniya dvuh posledovatel'nyh otklonenii v odnu i
tu zhe storonu:
kotoryi raven logarifmu otnosheniya dvuh posledovatel'nyh otklonenii v odnu i
tu zhe storonu:
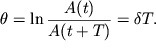 | (1.59) |
Iz (1.57), (1.58) i (1.59) nahodim:
| (1.60) |
Logarifmicheskii dekrement zatuhaniya mozhno ocenit', esli podschitat' chislo
kolebanii, sovershennyh sistemoi za vremya zatuhaniya ![]() to est' do
umen'sheniya amplitudy kolebanii primerno v 3 raza. Chem bol'she chislo etih
kolebanii, tem men'she poteri energii v sisteme.
to est' do
umen'sheniya amplitudy kolebanii primerno v 3 raza. Chem bol'she chislo etih
kolebanii, tem men'she poteri energii v sisteme.
Prosledim za ubyvaniem energii, zapasennoi oscillyatorom, s techeniem vremeni. Ispol'zuya (1.54), zapishem po analogii s (1.24) i (1.25) vyrazheniya dlya potencial'noi i kineticheskoi energii oscillyatora:
| (1.61) |
| (1.62) |
Zametim, chto, strogo govorya, skorost' ravna
| (1.63) |
Ochevidno, chto esli ![]() to pervym slagaemym v (1.63) mozhno
prenebrech' i zapisat' vyrazhenie dlya kineticheskoi energii v vide (1.62).
Summarnaya energiya oscillyatora ubyvaet so vremenem:
to pervym slagaemym v (1.63) mozhno
prenebrech' i zapisat' vyrazhenie dlya kineticheskoi energii v vide (1.62).
Summarnaya energiya oscillyatora ubyvaet so vremenem:
| (1.64) |
Primem vo vnimanie, chto pri ![]() chastota
chastota ![]() Tak kak
Tak kak ![]() to (1.64)
okonchatel'no zapishetsya v vide
to (1.64)
okonchatel'no zapishetsya v vide
| (1.65) |
Polnaya energiya oscillyatora, ravnaya vnachale ![]() monotonno ubyvaet so vremenem po eksponencial'nomu
zakonu i umen'shaetsya v e raz za vremya
monotonno ubyvaet so vremenem po eksponencial'nomu
zakonu i umen'shaetsya v e raz za vremya
| (1.66) |
"Kachestvo" kolebatel'noi sistemy harakterizuyut bezrazmernym parametrom ![]() nazyvaemym dobrotnost'yu. Dobrotnost' proporcional'na otnosheniyu zapasennoi
energii
nazyvaemym dobrotnost'yu. Dobrotnost' proporcional'na otnosheniyu zapasennoi
energii ![]() k energii
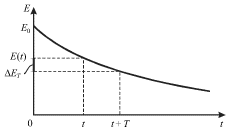
k energii ![]() teryaemoi za period (ris. 1.15):
teryaemoi za period (ris. 1.15):
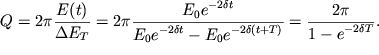 | (1.67) |
Esli chislo kolebanii veliko, to ![]() Togda
Togda
| (1.68) |
Pri eksponencial'nom zakone ubyvaniya energii so vremenem dobrotnost' ![]() okazyvaetsya postoyannoi velichinoi, kotoruyu, kak i logarifmicheskii dekrement
zatuhaniya
okazyvaetsya postoyannoi velichinoi, kotoruyu, kak i logarifmicheskii dekrement
zatuhaniya ![]() mozhno legko ocenit' po chislu kolebanii
mozhno legko ocenit' po chislu kolebanii ![]() sovershennyh sistemoi do ih polnogo prekrasheniya (za vremya
sovershennyh sistemoi do ih polnogo prekrasheniya (za vremya ![]() amplituda kolebanii umen'shaetsya v
amplituda kolebanii umen'shaetsya v ![]() raz, to est'
kolebaniya prakticheski polnost'yu zatuhayut).
raz, to est'
kolebaniya prakticheski polnost'yu zatuhayut).
 |
| Ris. 1.15. |
Sleduet otmetit', chto dobrotnost' ne tol'ko harakterizuet zatuhanie kolebanii, no i yavlyaetsya vazhnoi velichinoi, opredelyayushei parametry vynuzhdennyh kolebanii, osushestvlyaemyh pod deistviem vneshnei periodicheskoi sily (sm. dalee).
1Bolee podrobno metod kompleksnyh amplitud budet obsuzhdat'sya nizhe, pri rassmotrenii vynuzhdennyh kolebanii.|
Publikacii s klyuchevymi slovami:
kolebaniya - volny
Publikacii so slovami: kolebaniya - volny | |
|
Sm. takzhe:
| |