Astronet > Kolebaniya i volny

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Kolebaniya i volny. Lekcii.

V.A.Aleshkevich, L.G.Dedenko, V.A.Karavaev (Fizicheskii fakul'tet MGU)
Izdatel'stvo Fizicheskogo fakul'teta MGU, 2001 g. Soderzhanie

Rassmotrim teper' sluchai $\delta = \omega _{0},$ kogda korni harakteristicheskogo uravneniya kratnye: $\lambda _{1} = \lambda _{2} = - \delta .$ Pri etom chastota $\omega = \sqrt {\displaystyle \omega _{0}^{2} - \delta ^{2}} = 0,$ to est' kolebaniya otsutstvuyut. Obshee reshenie, kak netrudno proverit' podstanovkoi, imeet sleduyushii vid:

$s(t) = (s_{0} + Ct)e^{ - \delta t},$

(1.69)

gde nezavisimye postoyannye $s_{0}$ i $C$ opredelyayutsya, kak i ran'she, nachal'nymi usloviyami. Vozmozhnyi vid zavisimosti $s(t)$ pri raznyh nachal'nyh usloviyah izobrazhen na risunke 1.16.

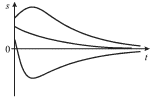Ris. 1.16.

Ih harakternoi osobennost'yu yavlyaetsya to, chto oni peresekayut os' Ot ne bolee odnogo raza, i vozvrat k ravnovesnomu sostoyaniyu u sistemy, vyvedennoi iz nego, proishodit za vremya poryadka neskol'kih $\tau .$ Takoi rezhim dvizheniya nazyvaetsya kriticheskim.

Nakonec, esli $\delta \gt \omega _{0},$ to obshee reshenie (1.52) yavlyaetsya summoi dvuh ubyvayushih s techeniem vremeni eksponent, poskol'ku - $\delta \pm \sqrt {\displaystyle \delta ^{2} - \omega _{0}^{2} } \lt 0.$ Vozmozhnyi vid zavisimostei $s(t)$ pohozh na to, chto izobrazheno na ris. 1.16, no vozvrat k ravnovesiyu osushestvlyaetsya medlennee, chem v kriticheskom rezhime, poskol'ku vyazkoe trenie bol'she. Dannyi rezhim dvizheniya nazyvaetsya aperiodicheskim, ili zakriticheskim.

Otmetim, chto naibolee bystroe vozvrashenie sistemy k polozheniyu ravnovesiya proishodit v kriticheskom rezhime, a v kolebatel'nom i aperiodicheskom rezhimah etot process dlitsya dol'she. Poetomu, naprimer, gal'vanometry - pribory dlya elektricheskih izmerenii - rabotayut obychno v rezhime, blizkom k kriticheskomu, kogda process ustanovleniya ih pokazanii, to est' smesheniya s ramki k ustoichivomu otkloneniyu $s_{ust},$ imeet naimen'shuyu dlitel'nost' (sm. ris. 1.17).

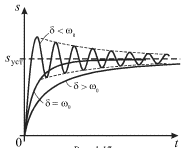Ris. 1.17.

Illyustraciei k rassmotrennym zakonomernostyam zatuhayushih kolebanii yavlyayutsya fazovye portrety, postroennye dlya kolebatel'nogo $(\delta \lt \omega _{0} ),$ a takzhe kriticheskogo i aperiodicheskogo $(\delta \ge \omega _{0} )$ rezhimov (ris. 1.18).

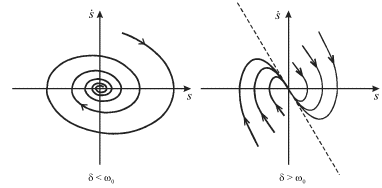Ris.1.18.

Pri $\delta \lt \omega _{0}$ fazovyi portret predstavlyaet soboi sovokupnost' spiralei, styagivayushihsya v osobuyu tochku tipa "fokus". Na ris. 1.18 izobrazhena odna iz takih spiralei. Za kazhdyi oborot radius spirali umen'shaetsya v $e^{\theta }$ raz. Dlya kriticheskogo i aperiodicheskogo rezhimov $\delta \ge \omega _{0}$ fazovye traektorii shodyatsya v osobuyu tochku tipa "uzel".

Zatuhanie kolebanii v sistemah s suhim treniem.

Na praktike my chasto imeem delo s sistemami, v kotoryh glavnuyu rol' igraet sila suhogo treniya, ne zavisyashaya ot skorosti. Tipichnyi primer - pruzhinnyi mayatnik, gruz kotorogo skol'zit po sherohovatoi gorizontal'noi poverhnosti, ili kolebatel'naya sistema u strelochnyh izmeritel'nyh priborov, osnovu kotoroi sostavlyaet vrashayushayasya ramka, ispytyvayushaya deistvie sil suhogo treniya v osi vrasheniya. Hotya sila $F_{tr}$ suhogo treniya i ne menyaetsya po velichine, tem ne menee ona menyaet svoe napravlenie pri izmenenii napravleniya skorosti. V silu etogo neobhodimo zapisat' dva uravneniya

$\ddot {\displaystyle s} + \omega _{0}^{2} s = - {\displaystyle \frac{\displaystyle {\displaystyle F_{tr} }}{\displaystyle {\displaystyle m}}}dlya \quad \dot {\displaystyle s} \gt 0;$

(1.70)

$\ddot {\displaystyle s} + \omega _{0}^{2} s = + {\displaystyle \frac{\displaystyle {\displaystyle F_{tr} }}{\displaystyle {\displaystyle m}}}dlya \quad \dot {\displaystyle s} \lt 0.$

(1.71)

Esli v (1.70) ispol'zovat' peremennuyu $s_{1} = s + {\displaystyle \frac{\displaystyle {\displaystyle F_{tr} }}{\displaystyle {\displaystyle m\omega _{0}^{2} }}},$ a v (1.71) - $s_{2} = s - {\displaystyle \frac{\displaystyle {\displaystyle F_{tr} }}{\displaystyle {\displaystyle m\omega _{0}^{2} }}},$ to oba uravneniya primut odinakovyi vid:

$\ddot {\displaystyle s}_{1,2} + \omega _{0}^{2} s_{1,2} = 0.$

(1.72)

Fazovye traektorii, sootvetstvuyushie etomu uravneniyu, predstavlyayut soboi ellipsy s centrami, imeyushimi koordinaty $s_{ - } = - {\displaystyle \frac{\displaystyle {\displaystyle F_{tr} }}{\displaystyle {\displaystyle m\omega _{0}^{2} }}} (s_{1} = 0)$ dlya verhnei poluploskosti $\dot {\displaystyle s} \gt 0,$ i $s_{ + } = + {\displaystyle \frac{\displaystyle {\displaystyle F_{tr} }}{\displaystyle {\displaystyle m\omega _{0}^{2} }}} (s_{2} = 0)$ dlya nizhnei poluploskosti $\dot {\displaystyle s} \lt 0.$ Chtoby narisovat' fazovyi portret, neobhodimo somknut' fazovye traektorii verhnei i nizhnei poluploskostei na ih obshei granice $\dot {\displaystyle s} = 0.$

Iz postroennogo na ris. 1.19 fazovogo portreta vidno, chto dvizhenie prekrashaetsya posle konechnogo chisla kolebanii. Chrezvychaino vazhno, chto sistema ne obyazatel'no pridet k sostoyaniyu $s = 0,$ a mozhet ostanovit'sya, popav v zonu zastoya $s_{ + } - s_{ - } .$ Zona zastoya tem bol'she, chem bol'she sila $F_{tr}$ . Iz fazovogo portreta legko opredelit' ubyvanie amplitudy kolebanii za odin period. Eto izmenenie amplitudy v dva raza prevyshaet protyazhennost' zony zastoya:

$\Delta A = A(t) - A(t + T) = 2(s_{ + } - s_{ - } ) = {\displaystyle \frac{\displaystyle {\displaystyle 4F_{tr} }}{\displaystyle {\displaystyle m\omega _{0}^{2} }}}.$

(1.73)

Takim obrazom, v otlichie ot eksponencial'nogo zakona (1.56), harakternogo dlya vyazkogo treniya, amplituda kolebanii ubyvaet so vremenem lineino.

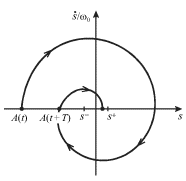Ris. 1.19.

Na ris. 1.20 pokazana zavisimost' ot vremeni smesheniya koleblyushegosya tela pri suhom trenii. Chislo sovershaemyh sistemoi kolebanii do ih prekrasheniya zavisit ot nachal'noi amplitudy $A_{0},$ i ego mozhno ocenit' po formule:

$N = {\displaystyle \frac{\displaystyle {\displaystyle A_{0} }}{\displaystyle {\displaystyle \Delta A}}} = {\displaystyle \frac{\displaystyle {\displaystyle A_{0} }}{\displaystyle {\displaystyle 2(s_{ + } - s_{\_} )}}}$

(1.74)

i zavisit ot nachal'noi amplitudy $A_{0} .$ Chastota kolebanii 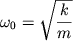$\omega _{0} = \sqrt {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle k}}{\displaystyle {\displaystyle m}}}}$ ostaetsya takoi zhe, kak i pri otsutstvii sily treniya (sm. (1.72)).

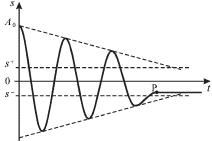Ris. 1.20.

Kolebaniya prodolzhayutsya do teh por, poka ih amplituda ostaetsya bol'she poloviny shiriny zony zastoya $s_{ + } - s_{ - } .$ Pri etom v real'nyh usloviyah koleblyushayasya massa ostanavlivaetsya v sluchainom polozhenii vnutri etoi zony (v tochke R na ris. 1.20).

Nazad| Vpered

Publikacii s klyuchevymi slovami: kolebaniya - volny Publikacii so slovami: kolebaniya - volny
Sm. takzhe: Eho iz glubin krasnogo giganta

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce