Astronet > Kolebaniya i volny

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Kolebaniya i volny. Lekcii.

V.A.Aleshkevich, L.G.Dedenko, V.A.Karavaev (Fizicheskii fakul'tet MGU)
Izdatel'stvo Fizicheskogo fakul'teta MGU, 2001 g. Soderzhanie

Vynuzhdennye kolebaniya pod deistviem garmonicheskoi sily. Rezhimy medlennyh, bystryh i rezonansnyh kolebanii. Amplitudno-chastotnye i fazo-chastotnye harakteristiki. Ballisticheskii rezhim kolebanii. Ustanovlenie kolebanii. Harakteristiki razlichnyh kolebatel'nyh sistem. Parametricheskie kolebaniya. Avtokolebaniya.

V predydushei lekcii my rassmotreli svobodnye zatuhayushie kolebaniya, voznikayushie pri nachal'nom kratkovremennom vozdeistvii vneshnih sil na kolebatel'nuyu sistemu. Mezhdu tem, v povsednevnoi praktike my stalkivaemsya s nezatuhayushimi kolebaniyami, dlya podderzhaniya kotoryh neobhodimo podvodit' energiyu k kolebatel'noi sisteme, chtoby kompensirovat' ee energeticheskie poteri.

Odnim iz rasprostranennyh sposobov podderzhaniya nezatuhayushih kolebanii yavlyaetsya nepreryvnoe vozdeistvie na koleblyushuyusya massu periodicheskoi sily (vynuzhdayushei sily)

$F(t) = F(t + T),$

(2.1)

menyayusheisya vo vremeni $t$ , voobshe govorya, proizvol'no v predelah perioda dlitel'nost'yu $T$ . Esli, naprimer, takuyu silu prilozhit' k koleblyusheisya masse opisannogo vyshe pruzhinnogo mayatnika (ris. 2.1), to uravnenie ee dvizheniya primet vid:

$m\ddot {\displaystyle s} = - \Gamma \dot {\displaystyle s} - ks + F(t).$

(2.2)

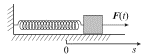Ris. 2.1.

Opyt pokazyvaet, chto esli sila vnezapno nachinaet deistvovat' (naprimer, v moment vremeni $t = 0$ ), to mayatnik nachnet postepenno raskachivat'sya, i spustya kakoe-to vremya ego kolebaniya ustanovyatsya. Po poryadku velichiny vremya ustanovleniya takih vynuzhdennyh kolebanii budet sovpadat' s vremenem zatuhaniya $\tau = \delta ^{ - 1} = 2m / \Gamma .$ Dalee my skoncentriruem vnimanie imenno na ustanovivshihsya kolebaniyah. Estestvenno, chto parametry takih kolebanii budut zaviset' ot konkretnogo vida sily $F(t).$ Iz matematiki horosho izvestno, chto lyubuyu periodicheskuyu funkciyu mozhno predstavit' v vide ryada Fur'e:

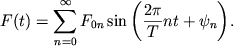$F(t) = {\displaystyle \sum\limits_{n = 0}^{\infty } {\displaystyle F_{0n} \sin \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle 2\pi }}{\displaystyle {\displaystyle T}}}nt + \psi _{n} } \right)} }.$

(2.3)

Fizicheskii smysl etogo predstavleniya sostoit v tom, chto periodicheskoe vozdeistvie $F(t)$ ekvivalentno odnovremennomu vozdeistviyu postoyannoi sily $F_{00}$ i nabora garmonicheskih sil s sootvetstvuyushimi amplitudami $F_{0n},$ nachal'nymi fazami $\psi _{n}$ i chastotami $\omega _{n} = {\displaystyle \frac{\displaystyle {\displaystyle 2\pi }}{\displaystyle {\displaystyle T}}}n = \omega n,$ kratnymi nizshei (osnovnoi) chastote $\omega = {\displaystyle \frac{\displaystyle {\displaystyle 2\pi }}{\displaystyle {\displaystyle T}}}.$

Chtoby poluchit' polnuyu kartinu vynuzhdennyh kolebanii pod deistviem sily (2.3), neobhodimo prinyat' vo vnimanie lineinost' uravneniya (2.2). Eto pozvolyaet predstavit' ego reshenie $s(t)$ kak summu garmonicheskih kolebanii:

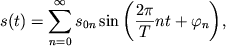$s(t) = {\displaystyle \sum\limits_{n = 0}^{\infty } {\displaystyle s_{0n} \sin \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle 2\pi }}{\displaystyle {\displaystyle T}}}nt + \varphi _{n} } \right)} },$

(2.4)

proishodyashih s ustanovivshimisya amplitudami $s_{0n}$ i fazami $\varphi _{n}$ na chastotah $\omega _{n}$ sootvetstvuyushih garmonik vynuzhdayushei sily (2.3). Kazhdoe slagaemoe v (2.4) mozhet rassmatrivat'sya kak vynuzhdennoe garmonicheskoe kolebanie, proishodyashee pod deistviem vneshnei garmonicheskoi sily s amplitudoi $F_{0n}$ i chastotoi $\omega _{n} = {\displaystyle \frac{\displaystyle {\displaystyle 2\pi }}{\displaystyle {\displaystyle T}}}n.$

Amplitudy $s_{0n}$ i fazy $\varphi _{n}$ trebuyut opredeleniya, i my pereidem seichas k ih nahozhdeniyu.

Vynuzhdennye kolebaniya pod deistviem garmonicheskoi sily.

Pust' vneshnyaya sila menyaetsya po garmonicheskomu zakonu

$F(t) = F_{0} \sin \omega t.$

(2.5)

Uravnenie (2.2) v etom sluchae prinimaet vid:

$m\ddot {\displaystyle s} = - \Gamma \dot {\displaystyle s} - ks + F_{0} \sin \omega t.$

(2.6)

Pod deistviem etoi sily mayatnik v ustanovivshemsya rezhime budet sovershat' garmonicheskie kolebaniya

$s(t) = s_{0} \sin (\omega t + \varphi _{0} ).$

(2.7)

Kak pokazyvaet opyt, amplituda $s_{0}$ i nachal'naya faza $\varphi _{0}$ (t.e. sdvig fazy mezhdu smesheniem $s$ i siloi $F$ ) ustanovivshihsya kolebanii zavisyat ne tol'ko ot amplitudy sily $F_{0}$ (chto ochevidno iz uravneniya (2.6)), no i ot togo, naskol'ko chastota vynuzhdayushei sily $\omega$ otlichaetsya ot sobstvennoi chastoty kolebanii mayatnika $\omega _{0} = \sqrt {\displaystyle k / m.}$ Naibolee sil'no mayatnik budet raskachivat'sya, kogda eti chastoty prakticheski sovpadayut: $\omega \approx \omega _{0} .$

Prezhde chem pristupit' k nahozhdeniyu $s_{0}$ i $\varphi _{0} ,$ zametim, chto dlya mehanicheskih kolebatel'nyh sistem ne tak prosto s tehnicheskoi tochki zreniya osushestvit' vozdeistvie garmonicheskoi sily neposredstvenno na dvizhushuyusya massu. Gorazdo proshe eto sdelat' dlya elektricheskih i opticheskih kolebatel'nyh sistem, naprimer, dlya kolebatel'nogo kontura, podklyuchennogo k vneshnemu istochniku peremennogo napryazheniya. Legko, odnako, videt', chto mozhno podderzhivat' vynuzhdennye kolebaniya mayatnika, izobrazhennogo na ris. 2.1, inym sposobom, ne prikladyvaya neposredstvenno vneshnyuyu silu $F(t)$ k masse $m.$ Dostatochno lish' etu silu prilozhit' k levomu koncu svobodnoi pruzhiny tak, chtoby etot konec dvigalsya po garmonicheskomu zakonu $\xi (t) = \xi _{0} \sin \omega t$ (ris. 2.2). Togda udlinenie pruzhiny sostavit velichinu $s - \xi ,$ a sila uprugosti, prilozhennaya k masse $m$ , budet ravna $- k(s - \xi ).$ Poetomu uravnenie dvizheniya massy $m$ zapishetsya v vide:

$m\ddot {\displaystyle s} = - \Gamma \dot {\displaystyle s} - k(s - \xi ).$

(2.8)

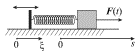Ris. 2.2.

Esli prinyat' vo vnimanie, chto sila uprugosti pruzhiny v otsutstvie smesheniya gruza (s = 0) ravna

$F(t) = k\xi (t) = k\xi _{0} \sin \omega t,$

(2.9)

to uravnenie (2.8) polnost'yu ekvivalentno uravneniyu (2.6). Sila (2.9) vypolnyaet rol' vneshnei garmonicheskoi sily v klassicheskoi sheme, izobrazhennoi na ris. 2.1. Eta sila legko mozhet byt' vizualizirovana, poskol'ku ee velichina i napravlenie odnoznachno opredelyaetsya smesheniem podvizhnogo levogo konca pruzhiny. Eto, v svoyu ochered', daet vozmozhnost' naglyadno prodemonstrirovat' fazovye sootnosheniya mezhdu siloi $F(t)$ (ili smesheniem $\xi (t)$ ) i smesheniem $s(t)$ koleblyusheisya massy.

Perepishem uravnenie (2.8) sleduyushim obrazom:

$\ddot {\displaystyle s} + 2\delta \dot {\displaystyle s} + \omega _{0}^{2} s = {\displaystyle \frac{\displaystyle {\displaystyle F_{0} }}{\displaystyle {\displaystyle m}}}\sin \omega t,$

(2.10)

gde $F_{0} = k\xi _{0} .$

Reshenie etogo uravneniya budem iskat' v vide garmonicheskogo kolebaniya (2.7), gde amplituda $s_{0}$ i faza $\varphi _{0}$ mogut byt' opredeleny, esli podstavit' (2.7) v (2.10). My sdelaem eto neskol'ko pozdnee, a poka rassmotrim tri vazhnyh rezhima vynuzhdennyh kolebanii.

Medlennye kolebaniya.

Esli chastota vynuzhdayushei sily $\omega$ znachitel'no men'she $\omega _{0} ,$ to skorost' $\dot {\displaystyle s}$ i uskorenie $\ddot {\displaystyle s}$ koleblyusheisya massy budut ochen' malymi. Poetomu mozhno prenebrech' pervymi dvumya chlenami v levoi chasti uravneniya (2.10) i zapisat' ego v priblizhennom vide:

$\omega _{0}^{2} s = {\displaystyle \frac{\displaystyle {\displaystyle F_{0} }}{\displaystyle {\displaystyle m}}}\sin \omega t.$

(2.11)

Ego reshenie ochevidno:

$s(t) = {\displaystyle \frac{\displaystyle {\displaystyle F_{0} }}{\displaystyle {\displaystyle m\omega _{0}^{2} }}}\sin \omega t = {\displaystyle \frac{\displaystyle {\displaystyle F_{0} }}{\displaystyle {\displaystyle k}}}\sin \omega t.$

(2.12)

V etom rezhime smeshenie gruza proporcional'no vneshnei sile i ne zavisit ot velichiny ego massy $m$ . Reshenie (2.12) yavlyaetsya, po sushestvu, matematicheskim vyrazheniem zakona Guka dlya staticheskoi deformacii pruzhiny. Poetomu etot rezhim mozhno nazvat' kvazistaticheskim (pochti staticheskim). Amplituda kolebanii v sootvetstvii s etim zakonom ravna $s_{0} = F_{0} / k,$ a smeshenie $s(t)$ izmenyaetsya v faze s vneshnei siloi.

V sheme, izobrazhennoi na ris. 2.2, eto ekvivalentno tomu, chto smeshenie massy $m$ prakticheski povtoryaet smeshenie levogo konca pruzhiny:

$s(t) = {\displaystyle \frac{\displaystyle {\displaystyle F_{0} }}{\displaystyle {\displaystyle k}}}\sin \omega t = {\displaystyle \frac{\displaystyle {\displaystyle k\xi _{0} }}{\displaystyle {\displaystyle k}}}\sin \omega t = \xi (t),$

(2.13)

poskol'ku $F_{0} = k\xi _{0} .$ Eto i ne udivitel'no, t.k. dlya dvizheniya massy $m$ s prenebrezhimo malym uskoreniem $\ddot {\displaystyle s}$ ne trebuetsya bol'shih deformacii pruzhiny: $s(t) - \xi (t) \approx 0.$

Nazad| Vpered

Publikacii s klyuchevymi slovami: kolebaniya - volny Publikacii so slovami: kolebaniya - volny
Sm. takzhe: Eho iz glubin krasnogo giganta

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

Kolebaniya i volny. Lekcii.

Lekciya 2

Vynuzhdennye kolebaniya pod deistviem garmonicheskoi sily.

Medlennye kolebaniya.