Astronet > Kolebaniya i volny

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Kolebaniya i volny. Lekcii.

V.A.Aleshkevich, L.G.Dedenko, V.A.Karavaev (Fizicheskii fakul'tet MGU)
Izdatel'stvo Fizicheskogo fakul'teta MGU, 2001 g. Soderzhanie

Esli $\omega \gg \omega _{0} ,$ to period vynuzhdennyh kolebanii $T = {\displaystyle {\displaystyle 2\pi } / {\displaystyle \omega }}$ mal. Eto oznachaet, chto massa $m$ ispytyvaet deistvie lish' vneshnei sily $F(t),$ a sila uprugosti $ks$ i vyazkogo treniya $\Gamma \dot {\displaystyle s}$ maly. Deistvitel'no, za polovinu korotkogo perioda kolebanii, kogda massa dvizhetsya v odnom napravlenii, ona ne uspevaet nabrat' kak zametnuyu skorost' $\dot {\displaystyle s},$ tak i smestit'sya na dostatochnoyu velichinu $s$ ot polozheniya ravnovesiya. Poetomu v uravnenii (2.10) mozhno opustit' chleny, soderzhashie $s$ i $\dot {\displaystyle s},$ i zapisat' ego v drugom priblizhennom vide:

$\ddot {\displaystyle s} = {\displaystyle \frac{\displaystyle {\displaystyle F_{0} }}{\displaystyle {\displaystyle m}}}\sin \omega t.$

(2.14)

Integriruya eto uravnenie dva raza, nahodim zakon dvizheniya koleblyusheisya massy:

$s(t) = - {\displaystyle \frac{\displaystyle {\displaystyle F_{0} }}{\displaystyle {\displaystyle m\omega ^{2}}}}\sin \omega t = {\displaystyle \frac{\displaystyle {\displaystyle F_{0} }}{\displaystyle {\displaystyle m\omega ^{2}}}}\sin (\omega t - \pi ).$

(2.15)

Iz (2.15) sleduet, chto smeshenie po otnosheniyu k vneshnei sile zapazdyvaet po faze na $\pi (\varphi _{0} = - \pi ),$ a amplituda, kak my i predpolagali, ubyvaet s uvelicheniem chastoty.

V sheme, izobrazhennoi na ris. 2.2, v takom rezhime levyi podvizhnyi konec pruzhiny i massa $m$ vsegda dvizhutsya v protivopolozhnyh napravleniyah:

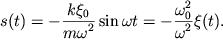$s(t) = - {\displaystyle \frac{\displaystyle {\displaystyle k\xi _{0} }}{\displaystyle {\displaystyle m\omega ^{2}}}}\sin \omega t = - {\displaystyle \frac{\displaystyle {\displaystyle \omega _{0}^{2} }}{\displaystyle {\displaystyle \omega ^{2}}}}\xi (t).$

(2.16)

Po absolyutnoi velichine smeshenie massy $m$ v ${\displaystyle {\displaystyle \omega ^{2}} / {\displaystyle \omega _{0}^{2} }} \gg 1$ raz men'she smesheniya levogo konca pruzhiny, t.e. prakticheski ne budet zametnym.

Rezonansnyi rezhim.

Esli chastota $\omega \approx \omega _{0} ,$ to vynuzhdennye kolebaniya proishodyat na sobstvennoi chastote kolebanii. Eto oznachaet, chto

$\ddot {\displaystyle s} + \omega _{0}^{2} s = 0.$

(2.17)

Sledovatel'no, uravnenie (2.10) pri uchete (2.17) primet vid:

$2\delta \dot {\displaystyle s} = {\displaystyle \frac{\displaystyle {\displaystyle F_{0} }}{\displaystyle {\displaystyle m}}}\sin \omega _{0} t.$

(2.18)

Integriruya ego, poluchaem vyrazhenie dlya smesheniya:

$s(t) = {\displaystyle \frac{\displaystyle {\displaystyle F_{0} }}{\displaystyle {\displaystyle 2\delta m\omega _{0} }}}\sin (\omega _{0} t - {\displaystyle {\displaystyle \pi } / {\displaystyle 2}}).$

(2.19)

Poslednee vyrazhenie udobno perepisat' v vide

$s(t) = {\displaystyle \frac{\displaystyle {\displaystyle F_{0} }}{\displaystyle {\displaystyle k}}}Q\sin (\omega _{0} t - {\displaystyle {\displaystyle \pi } / {\displaystyle 2),}}$

(2.20)

gde $Q = {\displaystyle \frac{\displaystyle {\displaystyle \pi }}{\displaystyle {\displaystyle \delta T}}}$ - dobrotnost' mayatnika. Esli dobrotnost' $Q \gg 1,$ to amplituda kolebanii mozhet vo mnogo raz prevyshat' amplitudu medlennyh kvazistaticheskih kolebanii (sr. s (2.12)). Poetomu takoi rezhim nazyvaetsya rezonansnym.

Veliki takzhe amplitudy skorosti i uskoreniya. Poskol'ku skorost' $\dot {\displaystyle s},$ kak sleduet iz (2.18), izmenyaetsya v faze s vneshnei siloi, to s energeticheskoi tochki zreniya eto ves'ma blagopriyatno dlya "podkachki" energii v kolebatel'nuyu sistemu. Rabota vneshnei sily za period kolebanii ravna:

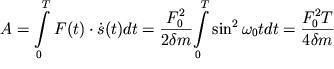$A = {\displaystyle \int\limits_{0}^{T} {\displaystyle F(t) \cdot \dot {\displaystyle s}(t)dt = {\displaystyle \frac{\displaystyle {\displaystyle F_{0}^{2} }}{\displaystyle {\displaystyle 2\delta m}}}} }{\displaystyle \int\limits_{0}^{T} {\displaystyle \sin ^{2}\omega _{0} tdt = {\displaystyle \frac{\displaystyle {\displaystyle F_{0}^{2} T}}{\displaystyle {\displaystyle 4\delta m}}}} }$

(2.21)

i znachitel'no prevoshodit rabotu etoi sily v oboih rassmotrennyh vyshe rezhimah. Takaya bol'shaya rabota neobhodima dlya kompensacii znachitel'nyh poter' iz-za sily vyazkogo treniya.

Dlya bol'shei naglyadnosti poslednego rezul'tata obratimsya k sheme s podvizhnym levym koncom pruzhiny, gde, kak eto vidno iz resheniya (2.20),

$s(t) = \xi _{0} Q\sin (\omega _{0} t - {\displaystyle {\displaystyle \pi } / {\displaystyle 2)}}.$

(2.22)

Amplituda smesheniya pravogo konca pruzhiny v $Q$ raz prevoshodit amplitudu smesheniya levogo konca. Pri prohozhdenii massoi $m$ polozheniya ravnovesiya $s = 0,$ kogda ee skorost' maksimal'na, levyi konec pruzhiny smeshen na maksimal'nuyu velichinu $\xi _{0}$ v napravlenii skorosti dvizhusheisya massy. V etot moment vremeni moshnost' sily uprugosti pruzhiny imeet maksimal'no vozmozhnoe polozhitel'noe znachenie pri zadannoi velichine $\xi _{0} .$ V posleduyushie momenty vremeni eta moshnost' budet ostavat'sya polozhitel'noi, chto, estestvenno, obespechivaet naibolee effektivnuyu peredachu energii dvizhushemusya s treniem telu.

Esli sila (2.5) menyaetsya s proizvol'noi chastotoi $\omega ,$ to amplituda $s_{0}$ i faza $\varphi _{0} ,$ vhodyashie v reshenie (2.7), mogut byt' naideny, kak bylo skazano vyshe, podstanovkoi resheniya (2.7) v uravnenie (2.10). Takuyu podstanovku mozhno osushestvit' naibolee prosto, esli vospol'zovat'sya metodom kompleksnyh amplitud, shiroko primenyaemym v razlichnyh oblastyah fiziki: teorii kolebanii, teorii voln, elektromagnetizme, optike i dr.

Metod kompleksnyh amplitud.

Esli v formule Eilera (1.53): $e^{i\varphi } = \cos \varphi + i\sin \varphi$ pod $\varphi$ ponimat' fazu garmonicheskih kolebanii

$\varphi = \omega t + \varphi _{0} ,$

(2.23)

to kazhdomu takomu kolebaniyu $s(t)$ mozhno postavit' v sootvetstvie kompleksnoe chislo

$\hat {\displaystyle s}(t) = s_{0} e^{i\varphi } = s_{0} e^{i\varphi _{0} }e^{i\omega t} = s_{0} \cos (\omega t + \varphi _{0} ) + is_{0} \sin (\omega t + \varphi _{0} )$

(2.24)

Iz (2.24) vidno, chto reshenie (2.7) yavlyaetsya mnimoi chast'yu kompleksnogo vyrazheniya:

$s(t) = s_{0} \sin (\omega t + \varphi _{0} ) = Im\hat {\displaystyle s}_{0} e^{i\omega t},$

(2.25)

gde $\hat {\displaystyle s}_{0} = s_{0} e^{i\varphi _{0} }$ - kompleksnaya amplituda, kotoraya neset informaciyu ob amplitude $s_{0}$ i nachal'noi faze $\varphi _{0}$ kolebanii. Nado otmetit', chto metod kompleksnyh amplitud yavlyaetsya, fakticheski, analiticheskim vyrazheniem metoda vektornyh diagramm. Esli v poslednem metode kolebanie s chastotoi $\omega$ polnost'yu zadaetsya vektorom ${\displaystyle \bf s_{0}} ,$ to v metode kompleksnyh amplitud kolebanie zadaetsya chislom $\hat {\displaystyle s}_{0}$ na kompleksnoi ploskosti. Poskol'ku s kompleksnymi chislami udobno i prosto proizvodit' matematicheskie operacii, to my ispol'zuem eto obstoyatel'stvo dlya polucheniya resheniya uravneniya vynuzhdennyh kolebanii (2.10).

Nazad| Vpered

Publikacii s klyuchevymi slovami: kolebaniya - volny Publikacii so slovami: kolebaniya - volny
Sm. takzhe: Eho iz glubin krasnogo giganta

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

Kolebaniya i volny. Lekcii.

Bystrye kolebaniya.

Rezonansnyi rezhim.

Metod kompleksnyh amplitud.