Astronet > Informaciya, termodinamika i konstrukciya biologicheskih sistem

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

INFORMACIYa, TERMODINAMIKA I KONSTRUKCIYa BIOLOGIChESKIH SISTEM

L.A.Blyumenfel'd (MGU im. M.V.Lomonosova)
Opublikovano v Sorosovskom obrazovatel'nom zhurnale, N 7, 1996 g. Soderzhanie

INFORMACIYa I ENTROPIYa

Za 20 let do poyavleniya rabot Shennona analizom informacii zanimalsya vengerskii fizik Scillard [Szillard L., 1929] v svyazi s resheniem odnogo termodinamicheskogo paradoksa, predlozhennogo Maksvellom eshe v proshlom veke [Maxwell J.C., 1971]. Smysl paradoksa Maksvella zaklyuchaetsya v sleduyushem (ris. 1). Izolirovannaya sistema, sostoyashaya iz razdelennogo na dve chasti rezervuara s gazom i s dvercei v peregorodke, soderzhit takzhe "demona" (sushestvo ili avtomat), nadelennogo sposobnost'yu otlichat' bystrye molekuly ot medlennyh. Demon otkryvaet dvercu tol'ko v tom sluchae, esli k nei sprava podletaet bystraya molekula. Poetomu gaz v levoi chasti rezervuara budet nagrevat'sya, a v pravoi - ostyvat'. Takim obrazom, v izolirovannoi sisteme teplo budet perehodit' ot holodnogo tela k goryachemu s ponizheniem entropii sistemy v protivorechii so vtorym zakonom termodinamiki.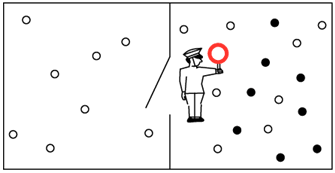

Ris. 1. Demon Maksvella.

Scillard [Szillard L., 1929], rassmotrev odin iz uproshennyh variantov paradoksa Maksvella, obratil vnimanie na neobhodimost' polucheniya informacii o molekulah i otkryl svyaz' mezhdu informaciei i termodinamicheskimi harakteristikami. V dal'neishem reshenie paradoksa Maksvella bylo predlozheno mnogimi avtorami (sm., naprimer, [Brillyuen L., 1960]). Smysl vseh reshenii zaklyuchaetsya v sleduyushem: informaciyu nel'zya poluchat' besplatno. Za nee prihoditsya platit' energiei, v rezul'tate chego entropiya sistemy povyshaetsya na velichinu, po krainei mere ravnuyu ee ponizheniyu za schet poluchennoi informacii. Pust' zadano makroskopicheskoe sostoyanie nekotoroi sistemy, to est' s opredelennoi stepen'yu tochnosti ukazany znacheniya takih parametrov, kak ob'em, davlenie, temperatura, himicheskii sostav i t.p. Kazhdomu makrosostoyaniyu sistemy sootvetstvuet nabor mikrosostoyanii. V mikrosostoyanii precizirovany (tochno zadany) sostoyaniya vseh chastic, vhodyashih v sistemu. Dlya lyuboi makrosistemy pri temperature vyshe absolyutnogo nulya chislo mikrosostoyanii W, sootvetstvuyushih dannomu makrosostoyaniyu, ogromno. W nazyvaetsya statisticheskim vesom ili termodinamicheskoi veroyatnost'yu dannogo makrosostoyaniya. Soglasno osnovnomu postulatu statisticheskoi fiziki, vse W mikrosostoyanii, sootvetstvuyushie odnomu makrosostoyaniyu, imeyut odinakovuyu apriornuyu veroyatnost'. Znat' mikrosostoyanie sistemy - znachit znat' o sisteme vse! Velichina W neposredstvenno svyazana s entropiei. Po formule Planka-Bol'cmana

$S = k\ln W$ ,

(3)

gde razmernaya postoyannaya Bol'cmana k = 1,38*10^-16 erg/grad ili 3,31*10^-24 ee (ee - entropiinaya edinica, 1 ee = 1 kal/grad). Rasschitaem, kakoe kolichestvo informacii nado poluchit' o sisteme, nahodyasheisya v dannom makrosostoyanii, chtoby odnoznachno opredelit' ee mikrosostoyanie. Inache govorya, kakogo kolichestva informacii nedostaet dlya polnogo opisaniya sistemy v zadannom makrosostoyanii? Pust' mikrosostoyanie opredeleno putem izmerenii ili raschetov (na samom dele sdelat' eto nel'zya). Do opredeleniya veroyatnost' togo, chto makroskopicheskaya sistema nahodilas' imenno v etom mikrosostoyanii, byla ravna 1/W, a posle opredeleniya stala ravnoi edinice. Poluchennoe kolichestvo informacii

$I = - \log_2 \frac{1}{W} = \log_2 W.$

(4)

Formuly (3) i (4) sovpadayut s tochnost'yu do postoyannogo razmernogo mnozhitelya. Velichiny I i S sushestvenno identichny. Situaciya zdes' ta zhe, chto i dlya sootnosheniya mezhdu massoi i energiei: E = mc², gde rol' razmernogo mnozhitelya igraet s². Analogichna situaciya i v sluchae sootnosheniya mezhdu chastotoi i energiei kvanta sveta, gde razmernym mnozhitelem yavlyaetsya postoyannaya Planka: $\epsilon = \hbar w$ . Entropiya sistemy v dannom makrosostoyanii est' kolichestvo informacii, nedostayushee do ee polnogo opisaniya. Chtoby pereiti ot kolichestva informacii v bitah k entropii v entropiinyh edinicah, neobhodimo pereiti ot logarifma pri osnovanii 2 k natural'nomu logarifmu i umnozhit' na k:

$S(ee) = 2,3 \cdot 10^{-24} I bit.$

(5)

Nazad | Vpered

Publikacii s klyuchevymi slovami: informaciya - entropiya - termodinamika Publikacii so slovami: informaciya - entropiya - termodinamika
Sm. takzhe: Golograficheskii princip i chainik Golograficheskii princip Informaciya Goryachie chernye dyry Matematicheskaya teoriya svyazi Entropiya bol'shogo kanonicheskogo ansamblya v rasshiryayusheisya Vselennoi Absolyutnaya temperatura

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce