Obychnye i neobychnye fazovye perehody
A. M. Skvorcov (Sankt-Peterburgskii himiko-farmacevticheskii institut)Opublikovano v Sorosovskom obrazovatel'nom zhurnale, N 8, 1996 g. Soderzhanie
Klassifikaciya fazovyh perehodov
Soglasno klassifikacii Erenfesta, sushestvuet dva tipa fazovyh perehodov - pervogo i vtorogo roda [Etkins P. ,1980]. Obychnye fazovye perehody, podobnye kipeniyu, plavleniyu ili vozgonke, soprovozhdayutsya skachkoobraznymi izmeneniyami vnutrennei energii i ob'ema (poglosheniem ili vydeleniem skrytogo tepla perehoda). Poskol'ku energiya i ob'em yavlyayutsya pervymi proizvodnymi ot svobodnoi energii po temperature i davleniyu, to pri etih fazovyh perehodah pervye proizvodnye svobodnoi energii yavlyayutsya razryvnoi funkciei. Eto posluzhilo osnovaniem nazvat' takie prevrasheniya fazovymi perehodami pervogo roda.
Perehody pervogo roda harakterizuyutsya beskonechno bol'shim vozrastaniem teploemkosti v ochen' uzkoi oblasti vokrug tochki perehoda. Fizicheskaya prichina etogo sostoit v tom, chto dobavlenie teploty k sisteme v tochke fazovogo perehoda ne povyshaet temperaturu sistemy, a rashoduetsya na perestroiku sistemy. V kachestve primera na risunke 1 pokazana temperaturnaya zavisimost' svobodnoi energii F, prihodyasheisya na odnu molekulu kristalla, pri ego prevrashenii v par. Verhnyaya vetv' otvechaet kristallicheskomu sostoyaniyu, a nizhnyaya vetv' predstavlyaet svobodnuyu energiyu paroobraznoi fazy. Pri nizkih temperaturah svobodnaya energiya kristalla men'she, chem para, i, sledovatel'no, kristallicheskoe sostoyanie vygodnee. Pri vysokih temperaturah, naoborot, vygodnee sushestvovanie paroobraznogo sostoyaniya. Shtrihovymi liniyami pokazany oblasti metastabil'nyh, termodinamicheski neustoichivyh sostoyanii sistemy. |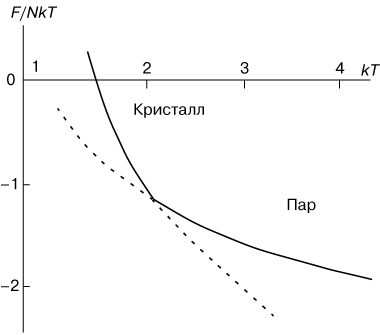
| Ris. 1. Temperaturnaya zavisimost' svobodnoi energii F pri fazovom perehode pervogo roda "par-kristall". |
Povedenie vnutrennei energii sistemy, prihodyasheisya na odnu molekulu, izobrazheno na risunke 2. Nizhnyaya vetv' otnositsya k kristallicheskomu sostoyaniyu, a verhnyaya k paroobraznomu. Skachok energii v tochke perehoda predstavlyaet soboi pogloshaemuyu skrytuyu teplotu. Sootvetstvenno teploemkost' v tochke fazovogo perehoda pervogo roda imeet "vsplesk".
 |
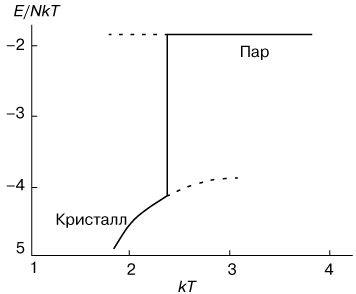| Ris. 2. Izmenenie energii E v zavisimosti ot temperatury T pri fazovom perehode pervogo roda "par-kristall". |
Pri teoreticheskom opisanii fazovyh perehodov pervogo roda kazhduyu iz faz obychno opisyvayut otdel'no. Tak, kristallicheskuyu vetv' rassmatrivayut, pol'zuyas' model'yu ideal'nogo kristalla, to est' predpolagaya regulyarnoe raspolozhenie vseh atomov. Paroobraznuyu zhe vetv' poluchayut, ispol'zuya model' ideal'nogo gaza, predpolagayushuyu polnyi besporyadok v sisteme. Zavisimosti, poluchennye dlya razlichnyh modelei, nakladyvayut drug na druga i issleduyut, kakaya iz vozmozhnostei realizuetsya v dannyh usloviyah. Poluchit' opisanie fazovogo perehoda pervogo roda, odnovremenno uchityvaya vse sostoyaniya sistemy, do nastoyashego vremeni ne udaetsya iz-za ogromnyh matematicheskih trudnostei.
Pri perehodah vtorogo roda vnutrennyaya energiya veshestva i ego ob'em ne izmenyayutsya v tochke perehoda i, sledovatel'no, ne proishodit vydeleniya ili poglosheniya skrytoi teploty. Odnako svobodnaya energiya sistemy pri fazovyh perehodah vtorogo roda imeet nekotoruyu osobennost', kotoraya proyavlyaetsya v tom, chto vtorye proizvodnye - teploemkost' i szhimaemost' - stanovyatsya beskonechnymi. Vyyavlenie haraktera etoi osobennosti - odna iz naibolee trudnyh zadach statisticheskoi fiziki. Sushestvuet vsego neskol'ko sistem, dlya kotoryh eta osobennost' byla vyyasnena. Odnoi iz takih sistem yavlyaetsya dvumernaya model' Izinga (model' dvumernogo ferromagnetika), rassmotrennaya L. Onsagerom [Landau L.D., Lifshic E.M.,1976 ]. Izmenenie energii ferromagnetika v dvumernoi modeli Izinga proishodit hotya i rezko, no bez skachkov (ris. 3). Pri etom teploemkost' sistemy obrashaetsya v beskonechnost' po logarifmicheskomu zakonu:
 |
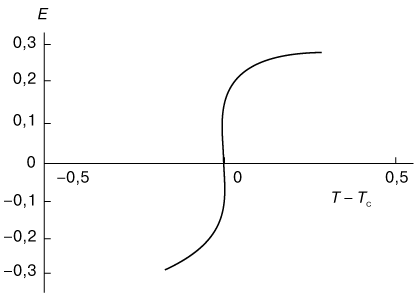| Ris. 3. Izmenenie energii E v zavisimosti ot temperatury T pri fazovom perehode vtorogo roda v dvumernoi modeli Izinga. |
 . | (1) |
Hod teploemkosti pokazan na risunke 4. Forma krivoi teploemkosti napominaet grecheskuyu bukvu
, poetomu takie perehody inogda nazyvayut -perehodami. Bystryi, no nepreryvnyi pod'em teploemkosti pokazyvaet, chto sistema nachinaet process svoei reorganizacii zadolgo do dostizheniya tochki perehoda. |
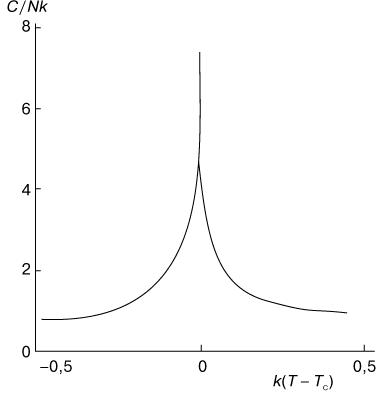| Ris. 4. Hod teploemkosti C v zavisimosti ot temperatury T pri fazovom perehode vtorogo roda v dvumernoi modeli Izinga. |
Fazovye perehody s tochki zreniya teorii Landau
Glubokii analiz problemy fazovyh perehodov byl sdelan L.D. Landau [Landau L.D., Lifshic E.M.,1976 ]. Soglasno teorii Landau, pri fazovyh perehodah pervogo roda funkciya raspredeleniya po energii ili plotnosti sistemy dolzhna byt' bimodal'noi, to est' imet' dva maksimuma. Naibolee vysokii maksimum otvechaet naibolee vygodnomu, stabil'nomu, sostoyaniyu sistemy, a vtoroi maksimum sootvetstvuet menee vygodnomu, metastabil'nomu, sostoyaniyu. V samoi tochke perehoda vysoty maksimumov stanovyatsya odinakovymi i sistema mozhet odnovremenno sosushestvovat' v oboih sostoyaniyah. Pri fazovyh perehodah vtorogo roda funkciya raspredeleniya vsegda imeet tol'ko odin maksimum, kotoryi rasshiryaetsya v tochke perehoda. Sootvetstvenno pri perehodah vtorogo roda metastabil'nyh sostoyanii v principe ne sushestvuet. K sozhaleniyu, imeetsya ochen' malo sistem, pozvolyayushih provesti strogoe statisticheskoe rassmotrenie i proverit' teoriyu Landau. Odnako, ispol'zuya komp'yutery, udalos' smodelirovat' fazovye perehody gaz-zhidkost'. Okazalos', chto v tochke fazovogo perehoda pervogo roda raspredelenie plotnosti deistvitel'no bimodal'no. Pri etom chem bol'she chislo chastic v sisteme, tem vyshe iguzhe piki na bimodal'noi krivoi. Dlya ochen' bol'shoi sistemy oblast' sosushestvovaniya dvuh faz prakticheski ischezaet i pri kazhdom znachenii vneshnih parametrov - temperatury i davleniya - my nablyudaem tol'ko odnu fazu, a sam fazovyi perehod proishodit skachkoobrazno v chrezvychaino uzkoi oblasti izmeneniya temperatury. S drugoi storony, v tochke fazovogo perehoda vtorogo roda, pri tak nazyvaemyh kriticheskih usloviyah funkciya raspredeleniya plotnosti rasshiryaetsya, no vsegda imeet tol'ko odin maksimum, kak i predpolagalos' v teorii Landau. Nalichie ili otsutstvie bimodal'nosti u funkcii raspredeleniya sluzhit vazhnym kriteriem, pozvolyayushim opredelit' rod perehoda. Obychno rech' idet o funkciyah raspredeleniya po energii sistemy ili po ee plotnosti, ili zhe po drugomu vazhnomu parametru, kotoryi nazyvayut parametrom poryadka sistemy. V poslednie gody bylo obnaruzheno, chto sushestvuyut sistemy, sposobnye sovershat' neobychnye fazovye prevrasheniya. Ih neobychnost' sostoit v tom, chto oni obladayut harakternymi chertami fazovyh perehodov pervogo i vtorogo rodov odnovremenno. Takie perehody svoistvenny molekulam polimerov. V kachestve primera my rassmotrim perehod, preterpevaemyi adsorbirovannoi polimernoi cep'yu pri ee otryvanii ot poverhnosti postoyannoi siloi. Takaya situaciya realizuetsya pri vneshnih vozdeistviyah na chasticy polimernogo kleya, skreplyayushego raznye poverhnosti. Poetomu rassmatrivaemaya zadacha imeet vazhnoe prakticheskoe znachenie dlya adgezii polimerov. Chtoby ponyat' sut' yavleniya, dostatochno rassmotret' uproshennuyu model' "lipkoi lenty".|
Publikacii s klyuchevymi slovami:
fazovyi perehod
Publikacii so slovami: fazovyi perehod | |
|
Sm. takzhe:
| |
