Astronet > Preodolenie difrakcionnogo predela v optike

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Preodolenie difrakcionnogo predela v optike

M. N. Libenson

Sankt-Peterburgskii gosudarstvennyi institut tochnoi mehaniki i optiki (tehnicheskii universitet)Soderzhanie

Eshe sovsem nedavno schitalos', chto predel vozmozhnomu v optike stavit fundamental'nyi releevskii kriterii razresheniya opticheskih priborov. On zaklyuchaetsya v tom, chto minimal'nyi razmer razlichimogo ob'ekta neskol'ko men'she dliny volny ispol'zuemogo sveta i principial'no ogranichen difrakciei izlucheniya. Odnako v poslednee vremya poyavilas' i vyzyvaet vse bol'shii interes vozmozhnost' izucheniya i formirovaniya opticheskimi metodami razlichnyh struktur nanometrovyh razmerov, kotorye vo mnogo raz men'she dliny svetovoi volny $\lambda$ . Takaya vozmozhnost' voznikla v svyazi s razvitiem blizhnepol'noi optiki (BPO) - novogo i chrezvychaino perspektivnogo napravleniya fizicheskoi i prikladnoi optiki. S fizicheskoi tochki zreniya ona osnovana na prisutstvii v dal'nei zone izlucheniya vpolne identificiruemyh sledov vzaimodeistviya sveta s mikroob'ektom, nahodyashimsya v blizhnem svetovom pole, kotoroe lokalizovano na rasstoyaniyah mnogo men'shih $\lambda$ . V tehnicheskom smysle BPO sochetaet elementy obychnoi optiki i skaniruyushei zondovoi mikroskopii. Otlichitel'nym elementom blizhnepol'nyh priborov yavlyaetsya opticheskii zond (ris. 1), obychno predstavlyayushii soboi zaostrennoe opticheskoe volokno 1, naruzhnaya poverhnost' kotorogo, za isklyucheniem vershiny konusa, pokryta neprozrachnym sloem metalla 2.

Chast' svetovogo potoka, rasprostranyayushegosya po voloknu, prohodit cherez vyhodnoe sechenie zonda kak skvoz' diafragmu v metallicheskom ekrane i dostigaet obrazca, raspolozhennogo v blizhnem pole istochnika. Esli rasstoyanie z do poverhnosti obrazca i radius a diafragmy udovletvoryayut usloviyu $a, z \ll \lambda$ , to razmer svetovogo pyatna na obrazce blizok k razmeru diafragmy. Pri peremeshenii zonda vdol' obrazca vozmozhna realizaciya razresheniya, ne ogranichennogo difrakciei, ili sverhrazresheniya.

Podobnaya ideya byla predlozhena eshe v 1928 godu Singhom (E.H. Syngh), ona namnogo operedila tehnicheskie vozmozhnosti svoego vremeni i ostalas' prakticheski ne zamechennoi. Ee pervoe podtverzhdenie bylo polucheno Eshem (E.A. Ash) v opytah s mikrovolnami v 1972 godu. V nachale 80-h godov gruppa issledovatelei iz Cyurihskoi laboratorii firmy IBM vo glave s Diterom Polem (D.W. Pohl) pronikla vnutr' difrakcionnogo predela i prodemonstrirovala razreshenie $\lambda$ /20 na pribore, rabotayushem v vidimom opticheskom diapazone i poluchivshem nazvanie blizhnepol'nogo skaniruyushego opticheskogo mikroskopa (BSOM). 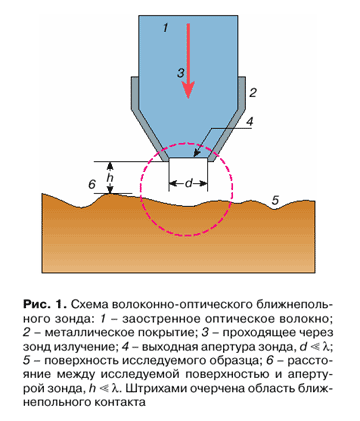Chut' ran'she v toi zhe laboratorii byl sozdan pervyi skaniruyushii tunnel'nyi mikroskop, prinesshii ei vsemirnuyu izvestnost'.

V otlichie ot tunnel'nogo i atomno-silovogo mikroskopov, srazu zavoevavshih priznanie, BSOM nekotoroe vremya ostavalsya v teni. Unikal'nye vozmozhnosti BSOM byli ubeditel'no prodemonstrirovany lish' v nachale 90-h godov, kogda udalos' reshit' dve vazhnye tehnicheskie problemy: sushestvenno povysit' energeticheskuyu effektivnost' zondov i obespechit' nadezhnyi kontrol' rasstoyaniya mezhdu ostriem i obrazcom. V poslednie gody v desyatkah laboratorii uspeshno vedutsya raboty po ispol'zovaniyu BSOM pri reshenii shirokogo kruga zadach fiziki poverhnosti, biologii, tehniki zapisi i schityvaniya informacii i dr. S 1993 goda v SShA vedetsya promyshlennyi vypusk priborov BPO.

Nizhe rassmotrena odna iz prosteishih shem blizhnepol'nogo mikroskopa, dano ob'yasnenie vozmozhnosti poluchit' sverhrazreshenie v optike ishodya iz pervyh principov, obsuzhdayutsya nekotorye primeneniya BPO. Fakticheski etu stat'yu mozhno rassmatrivat' kak vvedenie v blizhnepol'nuyu optiku.

Blizhnepol'nyi mikroskop

K nastoyashemu vremeni sozdano okolo 20 tipov BSOM, razlichayushihsya osobennostyami opticheskoi shemy i funkcional'nym naznacheniem zonda. V zavisimosti ot nalichiya ili otsutstviya diafragmy na konce zonda ih mozhno razbit' na dve osnovnye gruppy: aperturnye i bezaperturnye. Princip deistviya aperturnyh BSOM, sostavlyayushih preobladayushee bol'shinstvo sovremennyh priborov, poyasnyaet privedennaya na ris. 2 blok-shema mikroskopa.

Luch lazera (obychno gelii-neonovogo ili argonovogo) cherez soglasuyushii element popadaet v zaostrennoe metallizirovannoe volokno i na vyhode suzhaetsya do razmerov diafragmy. Vzaimnoe peremeshenie ostriya i obrazca v treh izmereniyah x, y, z osushestvlyaetsya s pomosh'yu p'ezodvizhitelei. Proshedshie cherez obrazec ili otrazhennye i rasseyannye fotony ulavlivayutsya odnim iz mikroob'ektivov (2 ili 1 sootvetstvenno, sm. ris. 2) i napravlyayutsya v registriruyushii pribor, obychno fotoumnozhitel'. 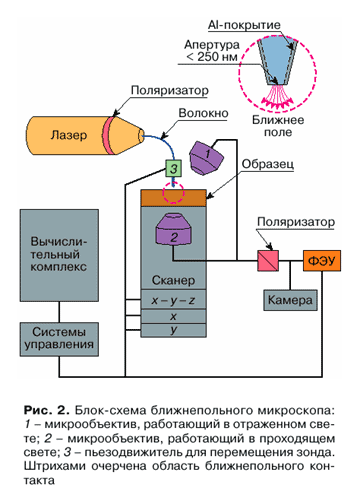Takoi mikroob'ektiv, kak pravilo, vhodit v shemu obyknovennogo opticheskogo mikroskopa, chto pozvolyaet osushestvit' vybor issleduemogo uchastka i ego privyazku k bolee shirokomu polyu. Privedennaya na ris. 2 shema otnositsya k priboram, rabotayushim v rezhime osvesheniya (illumination mode). Shiroko rasprostraneny pribory, rabotayushie v rezhime sbora fotonov (collection mode), kogda zond perenosit fotony ot obrazca, osveshennogo, naprimer, cherez mikroob'ektiv, k detektoru. V kombinirovannom rezhime (osveshenie / sbor) zond vypolnyaet odnovremenno obe funkcii.

Chtoby ustanovit' ostrie na nuzhnoi vysote nad obrazcom, vo vseh skaniruyushih zondovyh mikroskopah ispol'zuyut zavisimost' velichiny I registriruemogo signala ot z. V bol'shinstve tipov BSOM zavisimost' I(z) neodnoznachna, poskol'ku naryadu s blizhnepol'nym signalom I₁ registriruetsya takzhe periodicheski izmenyayushiisya s z signal I₂ , vyzvannyi interferenciei padayushei i pereotrazhennyh v sisteme zond-obrazec voln. Eto zatrudnyaet ili delaet polnost'yu nevozmozhnym nadezhnyi kontrol' z po velichine I = I₁ + I₂ pri sblizhenii ostriya s obrazcom. Luchshim resheniem problemy yavlyaetsya vvedenie v BSOM vspomogatel'nyh uzlov, pozvolyayushih im osushestvlyat' takzhe funkcii skaniruyushego tunnel'nogo ili atomno-silovogo mikroskopov, v kotoryh opredelenie z ne vyzyvaet sushestvennyh trudnostei. V takih kombinirovannyh priborah zapis' izobrazheniya osushestvlyaetsya odnovremenno po dvum kanalam, odin iz kotoryh vosproizvodit rel'ef poverhnosti, a drugoi - lokal'noe raspredelenie pokazatelya prelomleniya v tonchaishem pripoverhnostnom sloe. Vozmozhnost' razlicheniya opticheskogo i topograficheskogo kontrastov sushestvenno uproshaet interpretaciyu izobrazheniya. Naibol'shee rasprostranenie poluchil metod kontrolya z, osnovannyi na izmenenii tangencial'noi sostavlyayushei sily fizicheskogo vzaimodeistviya ostriya s obrazcom (shear force).

Razreshayushaya sposobnost' blizhnepol'nyh mikroskopov

Osnovnoi harakteristikoi BSOM yavlyaetsya prostranstvennoe razreshenie, kotoroe v sil'noi stepeni zavisit ot uslovii osvesheniya ili v bolee obshem sluchae - ot nablyudeniya obrazca, struktury ego poverhnosti i mikrogeometrii zonda. Izvestno, chto funkciya impul'snogo otklika difrakcionno-ogranichennoi opticheskoi sistemy opisyvaetsya raspredeleniem Eri. Polushirina glavnogo maksimuma raspredeleniya sootvetstvuet razresheniyu po Releyu: $\Delta x = 0,61\lambda / \sin \phi$ , gde $\phi$ - aperturnyi ugol. V predele pri $\phi \to \pi /2$ $\Delta x \to \Delta x_min = 0,61\lambda$ . Pri prohozhdenii sveta cherez maluyu diafragmu iz-za rasseyaniya i geometricheskih ogranichenii proishodit iskazhenie i rasshirenie $\Delta f$ spektra perenosimyh prostranstvennyh chastot, kotoroe takzhe opisyvaetsya raspredeleniem Eri $\Delta f = 0,61/a$ . V rezul'tate pri $a \to 0$ volnovoe pole neposredstvenno za diafragmoi soderzhit skol' ugodno bol'shie prostranstvennye chastoty i kak sledstvie etogo $\Delta x_min \to 0$ . V real'noi situacii iz-za konechnoi pronicaemosti metallicheskogo ekrana (pokrytiya) minimal'nyi effektivnyi radius diafragmy opredelyaetsya glubinoi proniknoveniya sveta v metall ili tolshinoi $\delta$ skin-sloya. S uchetom etogo ozhidaemoe predel'noe razreshenie, naprimer, dlya zonda s alyuminievym pokrytiem v vidimom diapazone spektra sostavlyaet $\Delta x_min \approx 2\delta \approx 13$ nm, chto sootvetstvuet luchshim eksperimental'nym rezul'tatam. Otsutstvie fizicheskih ogranichenii razmera vershiny zonda v bezaperturnyh BSOM pozvolyaet realizovat' v nih razreshenie luchshe 1 nm.

Chto takoe blizhnee pole

Kriterii Releya yavlyaetsya odnoi iz illyustracii principa neopredelennosti Geizenberga, soglasno kotoromu lyubaya popytka povysit' stepen' lokalizacii ili tochnost' opredeleniya polozheniya $\Delta x$ istochnika sveta privodit k vozrastaniyu neopredelennosti $\Delta p_x$ sopryazhennogo impul'sa fotonov. Pri rasseyanii fotonov v maksimal'nom diapazone uglov $-\pi /2 \le \phi \le \pi /2 \Delta p_x = \hbar \Delta k_x = 4\pi \hbar /\lambda$ ( $\hbar$ - postoyannaya Planka, k_x - x-komponenta volnovogo vektora k) i $\Delta x \ge \lambda /2$ . Vozmozhnost' realizacii razresheniya $\Delta x \ll \lambda /2$ , kazalos' by, protivorechit odnomu iz osnovnyh fizicheskih principov. Sleduet, odnako, imet' v vidu, chto sootnoshenie neopredelennosti v samom obshem vide otnositsya k polozheniyu chasticy v impul'sno-koordinatnom prostranstve. Poetomu, ogranichivaya odnu iz komponent volnovogo vektora, ono pozvolyaet var'irovat' drugie. Mozhno prinyat', naprimer, $k_y = 0$ , $k_z = -i \gamma$ , gde $\gamma$ - veshestvennoe polozhitel'noe chislo. Togda Pri $\gamma \to \infty$ oblast' dopustimyh znachenii k_x neogranichenno rastet, a $\Delta x$ mozhet byt' skol' ugodno malym.

Mnimym k_z sootvetstvuyut zatuhayushie volny. Sledovatel'no, pri realizacii subvolnovogo razresheniya antenna-zond dolzhna raspolagat'sya v predelah zatuhayushego polya vblizi poverhnosti obrazca, to est' zavedomo pri $z \le \lambda$ .

My mozhem teper' utochnit' ponyatie blizhnego polya, associiruya ego s oblast'yu sushestvovaniya zatuhayushih i, sledovatel'no, neradiacionnyh voln, amplituda kotoryh menyaetsya s rasstoyaniem z ot granicy razdela sred ili malogo rasseivayushego ob'ekta po zakonu $E(z) = E(0)exp(-gz)$ , gde g > 0. Velichina g^-1 harakterizuet glubinu proniknoveniya zatuhayushei volny i po poryadku soizmerima s razmerami subvolnovogo rasseivatelya. V chastnosti, dlya diafragmy radiusa a v tonkom provodyashem ekrane $g^{-1} \approx 2a$ . Dlya poverhnosti so slozhnym rel'efom velichina g^-1 opredelyaetsya summarnym vkladom komponent spektra prostranstvennyh chastot, prichem m-ya komponenta s periodom $d^m \ll \lambda$ obnaruzhima na rasstoyanii $z\le \gamma^{-1}_m \approx d_m / (2\pi).$ (V rezhime sbora fotonov tochnost' vosproizvedeniya profilya poverhnosti vozrastaet s uvelicheniem chisla m komponent zatuhayushego polya, uchastvuyushih v obrazovanii izobrazheniya, a znachit, s umen'sheniem z.) V dal'nem pole pri $z \ge \lambda$ prisutstvuyut lish' rasprostranyayushiesya volny, k kotorym primenimy zakony i ogranicheniya obychnoi optiki. Estestvenno, chto oni takzhe vnosyat vklad v rezul'tiruyushee pole v blizhnei volnovoi zone. Strukturu blizhnego polya mogut opredelyat' takzhe i razlichnogo roda poverhnostnye rezonansnye elektromagnitnye mody, vozbuzhdaemye svetom vblizi vyhodnogo secheniya zonda (naprimer, poverhnostnye polyaritony, o kotoryh uzhe pisalos' v nashih predydushih stat'yah v "Sorosovskom Obrazovatel'nom Zhurnale").

Reshenie zadachi o prohozhdenii sveta cherez diafragmu radiusom $a \ll \lambda$ v beskonechno tonkom provodyashem ekrane bylo vpervye polucheno G. Bete. Okazalos', chto diafragma takogo razmera propuskaet znachitel'no men'she sveta, chem mozhno ozhidat', ekstrapoliruya rezul'taty rascheta pri $a > \lambda$ . V chastnosti, sechenie rasseyaniya $\sigma$ nepolyarizovannogo sveta svyazano s velichinoi a i volnovym chislom $k = 2\pi /\lambda$ sootnosheniem

$\sigma = \frac{64}{27 \pi}k^4 a^6 (1 - \frac{3}{8}sin^2\Theta ),$

gde $\Theta$ - ugol padeniya izlucheniya.

Formula (1) pomimo chislennogo koefficienta otlichaetsya ot ispol'zuemoi v raschetah po metodu Kirhgofa dopolnitel'nym mnozhitelem $(ka)^2 \ll 1$ . Razlichie vyzvano tem, chto znachitel'naya chast' elektromagnitnoi energii perehodit v neradiacionnuyu formu, kotoraya ne mozhet byt' vosprinyata udalennym nablyudatelem. S tochki zreniya takogo nablyudatelya, diafragma rasseivaet svet kak para vzaimno perpendikulyarnyh dipolei: elektricheskogo, napravlennogo vdol' osi diafragmy, i magnitnogo, momenty kotoryh ravny sootvetstvenno

$\vec \mu_e = \frac{a^3}{3\rho } \vec E_0,$ $\vec \mu_m = -\frac{2a^3}{3\rho }\vec H_0,$

gde $\vec E_0, \vec H_0$ - elektricheskii i magnitnyi vektory polya pered ekranom. Chisto kachestvenno formula (2) spravedliva takzhe i v sluchae, kogda vmesto diafragmy vystupaet sfera radiusa a; pri etom dlya kolichestvennogo sovpadeniya neobhodimo polozhit', chto dielektricheskaya pronicaemost' materiala sfery $\epsilon \approx 2$ .

Nazad | Vpered

Publikacii s klyuchevymi slovami: difrakcionnyi predel - difrakciya sveta - optika - razreshenie - Mikroskop - opticheskie pribory Publikacii so slovami: difrakcionnyi predel - difrakciya sveta - optika - razreshenie - Mikroskop - opticheskie pribory
Sm. takzhe: Na difrakcionnom predele Raduzhnoe oblako nad Ogaio Tumannoe koromyslo nad Kaliforniei Refraktor memorial'noi observatorii im. Krosbai Remseya Laboratoriya issledovaniya zvezdnogo magnetizma SAO RAN Svet, poimannyi v veshestve Laboratoriya metodov astronomii vysokogo razresheniya SAO RAN Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

Preodolenie difrakcionnogo predela v optike

M. N. Libenson

Vvedenie

Blizhnepol'nyi mikroskop

Razreshayushaya sposobnost' blizhnepol'nyh mikroskopov

Chto takoe blizhnee pole