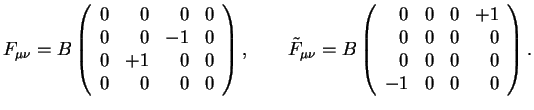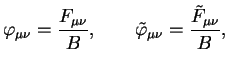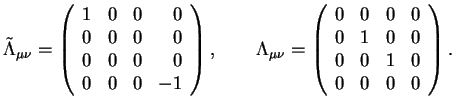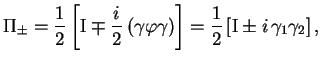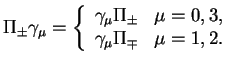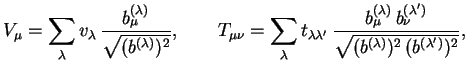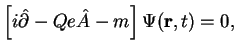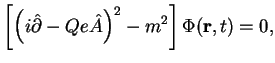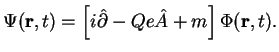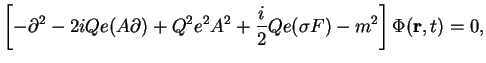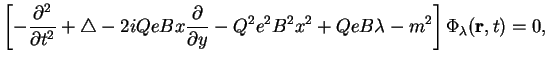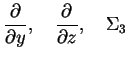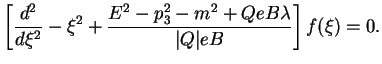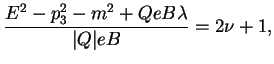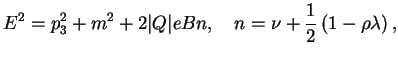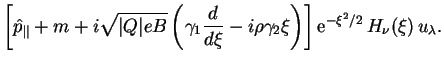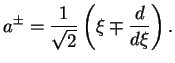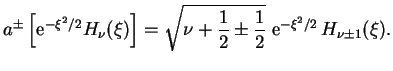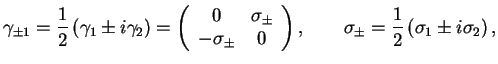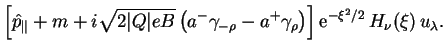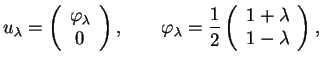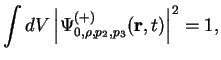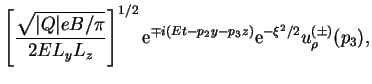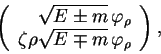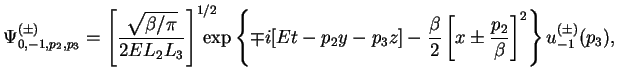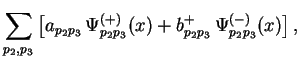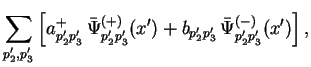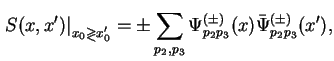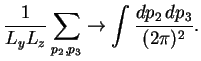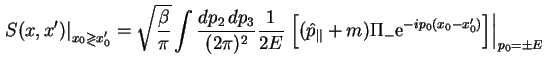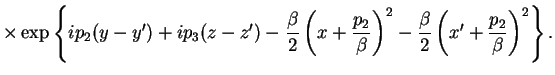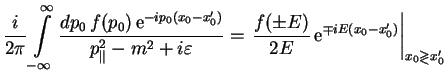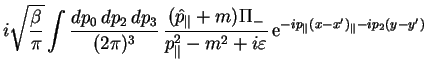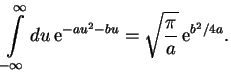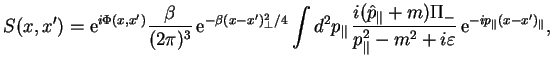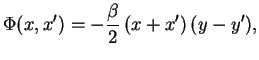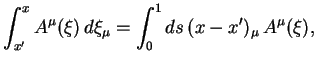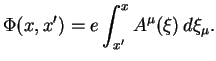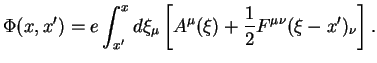Zadaniya po kvantovoi teorii polya

---

<< Titul'nyi list | Oglavlenie | Drevesnye processy >>

Vvodnye zadaniya

(Zadanie 1, Zadanie 2, Zadanie 3)

Zadanie 1. Postroit' bazis dlya chasticy v postoyannom odnorodnom magnitnom pole.

Reshenie. Dlya lyuboi chasticy s impul'som , nahodyasheisya v elektromagnitnom pole, mozhno vvesti udobnyi dlya analiza kvantovyh processov s ee uchastiem bazis. Zametim, chto konfiguraciya chisto magnitnogo polya, naibolee vazhnaya v prilozhenii k astrofizicheskim ob'ektam, obladaet naborom specificheskih svoistv, ispol'zovanie kotoryh sushestvenno uproshaet raschety konkretnyh reakcii.

Iz elektrodinamiki izvestno, chto elektromagnitnoe pole polnost'yu opredelyaetsya tenzorom napryazhennostei . V dopolnenie k nemu takzhe vvoditsya dual'no sopryazhennyi tenzor . Vyberem sistemu koordinat takim obrazom, chtoby os' byla napravlena vdol' napryazhennosti magnitnogo polya . V takoi sisteme otscheta tenzory i imeyut sleduyushii yavnyi vid:

V dal'neishem udobno pol'zovat'sya ne samim tenzorom elektromagnitnogo polya i dual'nym k nemu, a ih bezrazmernymi analogami:

yavnyi vid kotoryh v vybrannoi nami sisteme otscheta predstavlen chislovymi matricami v formule (1.1).

Predstavlyaet interes proanalizirovat' algebru vvedennyh bezrazmernyh tenzorov (1.2). Nachnem s binarnyh proizvedenii:

V otlichie ot antisimmetrichnyh tenzorov i , tenzory i simmetrichny v sootvetstvii s obshimi svoistvami svertok tenzorov. V vybrannoi nami sisteme koordinat eti tenzory imeyut sleduyushii yavnyi vid:

Iz yavnogo predstavleniya tenzorov vidno, chto oni ne yavlyayutsya lineino nezavisimymi, a svyazany drug s drugom posredstvom metricheskogo tenzora :

Provedennyi analiz pokazyvaet, chto nalichie postoyannogo odnorodnogo vneshnego magnitnogo polya estestvennym obrazom razbivaet chetyrehmernoe prostranstvo Minkovskogo na dva neperesekayushihsya podprostranstva: dvumernoe evklidovo podprostranstvo s metricheskim tenzorom , ortogonal'noe vektoru napryazhennosti magnitnogo polya B, i dvumernoe psevdoevklidovo podprostranstvo s metricheskim tenzorom . Bezrazmernye tenzory elektromagnitnogo polya i igrayut rol' tenzorov Levi-Chivita (polnost'yu antisimmetrichnyh tenzorov) etih podprostranstv i obladayut sleduyushimi svoistvami:

Dlya vvedennogo nabora tenzorov spravedlivy sleduyushie binarnye sootnosheniya:

Pri konkretnyh vychisleniyah okazyvaetsya udobnym vvesti special'nye oboznacheniya dlya kazhdogo iz podprostranstv: - dlya evklidova podprostranstva s metrikoi i - dlya psevdoevklidova podprostranstva s metrikoi . Pri takom soglashenii proizvol'nyi 4-vektor mozhno razbit' na dve ortogonal'nye sostavlyayushie:

gde i v sootvetstvii so svoistvom (1.5). Takoe razbienie pozvolyaet vvesti skalyarnoe proizvedenie vektorov v kazhdom podprostranstve po otdel'nosti:

gde i - proizvol'nye 4-vektory.

Delenie chetyrehmernogo prostranstva na dva neperesekayushihsya podprostranstva privodit k effektivnoi modifikacii svoistv -matric. Budem oboznachat' -matricy podprostranstva kak , a podprostranstva - . Vvedem proekcionnye operatory :

gde uchten yavnyi vid tenzora v vybrannoi sisteme otscheta. Otmetim sleduyushie mul'tiplikativnye svoistva proekcionnyh operatorov:

a takzhe ih kommutacionnye svoistva po otnosheniyu k -matricam:

Poslednee svoistvo interesno tem, chto esli vstrechaetsya konstrukciya vida , to effektivno ot -matricy ostaetsya tol'ko ee prodol'naya sostavlyayushaya - . Sleduet otmetit' takzhe i kommutativnost' proekcionnyh operatorov s matricei :

Shiroko ispol'zuemoi operaciei yavlyaetsya vzyatie shpura proizvedeniya nekotorogo chisla -matric. V sluchae sil'nogo magnitnogo polya vychislenie shpurov effektivno realizuetsya tol'ko v podprostranstve. Kak i v obychnom chetyrehmernom prostranstve v podprostranstve shpur nechetnogo chisla -matric raven nulyu, a neskol'ko pervyh shpurov chetnogo chisla - sleduyushie:

Polezny i drugie chasto vstrechayushiesya sootnosheniya:

Legko pokazat', chto svertka dvuh -matric, mezhdu kotorymi nahoditsya lyuboe nechetnoe chislo -matric, obrashaetsya v nul'.

Nalichie vneshnego magnitnogo polya, a sledovatel'no, i nabora tenzorov , , i pozvolyaet estestvennym obrazom vvesti bazis chetyrehmernogo impul'snogo prostranstva dlya lyuboi chasticy s 4-impul'som :

Eti vektory vzaimno ortogonal'ny, no ne normirovany, poetomu privedem znacheniya kvadratov etih vektorov:

Otsyuda vidno, chto ortonormirovannyi bazis mozhet byt' legko postroen kak dlya vremenipodobnogo , tak i dlya prostranstvennopodobnogo vektora. Dlya bezmassovoi chasticy na massovoi poverhnosti () tretii i chetvertyi bazisnye vektory okazyvayutsya izotropnymi, chto ne pozvolyaet ih normirovat'. Odnako eto ne meshaet pol'zovat'sya naborom nenormirovannyh bazisnyh vektorov (1.17) pri raschetah processov s uchastiem bezmassovyh chastic. Sleduet takzhe otmetit', chto pervyi i vtoroi bazisnye vektory celikom lezhat v i podprostranstvah sootvetstvenno, v to vremya kak tretii i chetvertyi imeyut sostavlyayushie v oboih podprostranstvah. Vypishem yavnyi vid nabora bazisnyh vektorov v vybrannoi nami sisteme otscheta:

Vvedenie bazisa (1.17) pozvolyaet delat' razlozheniya 4-tenzora lyubogo ranga v sootvetstvii s pravilami:

gde i - proizvol'nye 4-vektor i 4-tenzor vtorogo ranga, a i - ih sostavlyayushie v etom bazise.

Zadanie 2. Naiti reshenie uravneniya Diraka dlya fermiona s zaryadom ( - elementarnyi zaryad) v postoyannom odnorodnom vneshnem magnitnom pole.

Reshenie. Uravnenie Diraka dlya fermiona vo vneshnem elektromagnitnom pole s 4-potencialom  imeet vid:

gde i .

Resheniya etogo uravneniya, poluchennye dlya postoyannogo odnorodnogo magnitnogo polya , poluchili svoe naibol'shee prilozhenie v astrofizike. V chastnosti, na poverhnosti pul'sarov obnaruzheny dostatochno sil'nie magnitnye polya  Gs, a soglasno teoreticheskim modelyam v yadrah takih pul'sarov napryazhennosti polei mogut byt' na dva-tri poryadka bol'she. V etoi svyazi neposredstvennyi interes predstavlyayut ne prosto tochnye resheniya uravneniya Diraka v magnitnom pole, a ih asimptotika v sluchae ekstremal'no bol'shih napryazhennostei.

Dlya resheniya uravneniya (2.1) vyberem sistemu koordinat takim obrazom, chtoby vektor napryazhennosti magnitnogo polya B byl napravlen po osi , a vektornyi potencial A - po osi . V takoi kalibrovke 4-potencial vneshnego magnitnogo polya mozhno predstavit' v vide:

Dlya resheniya postavlennoi zadachi udobno vvesti vspomogatel'nuyu funkciyu , kotoraya yavlyaetsya resheniem kvadrirovannogo uravneniya Diraka:

pri etom tochnoe reshenie uravneniya (2.1) svyazano s funkciei sootnosheniem:

Naidem yavnyi vid funkcii  . Ispol'zuya izvestnoe svoistvo proizvedeniya dvuh -matric - , gde - metricheskii tenzor i , a takzhe uslovie Lorenca dlya 4-potenciala - , kvadrirovannoe uravnenie (2.3) privoditsya k vidu:

gde - tenzor vneshnego magnitnogo polya, i . Mozhno pokazat', chto , gde - proekciya relyativistskogo operatora spina fermiona na os' . Budem schitat', chto funkciya yavlyaetsya sobstvennoi funkciei operatora :

gde sobstvennoe znachenie imeet smysl udvoennogo srednego znacheniya proekcii spina fermiona. Togda operator v kvadrirovannom uravnenii (2.5) stanovitsya proporcional'nym edinichnoi matrice prostranstva Diraka, chto pozvolyaet fakticheski pereiti ot matrichnogo k skalyarnomu uravneniyu. Prinimaya vo vnimanie yavnyi vid 4-potenciala (2.2), raspishem yavno kvadrirovannoe uravnenie (2.5) v vybrannoi nami sisteme koordinat:

gde - operator Laplasa. Operator uravneniya (2.7) ne zavisit yavno ot vremeni, poetomu funkciya yavlyaetsya stacionarnym resheniem etogo uravneniya i opisyvaet kvantovuyu chasticu s sohranyayushimsya znacheniem energii . Poskol'ku privedennoe uravnenie (2.7) imeet yavnuyu zavisimost' tol'ko ot peremennoi , to operator etogo uravneniya budet kommutirovat' s operatorami i . Eti differencial'nye operatory opredeleny v lorencevskom 4-prostranstve-vremeni, poetomu oni takzhe budut kommutirovat' i s operatorom , yavlyayushimsya postoyannoi velichinoi v etom prostranstve. Ishodya iz vysheskazannogo, budem iskat' polozhitel'no chastotnoe reshenie uravneniya (2.7) v vide:

kak sobstvennuyu funkciyu treh operatorov:

s sobstvennymi znacheniyami , i sootvetstvenno. Budem takzhe schitat', chto postoyannyi bispinor yavlyaetsya resheniem uravneniya (2.6).

Podstavlyaya reshenie (2.8) v uravnenie (2.5) i vvodya vmesto  novuyu bezrazmernuyu peremennuyu , poluchim sleduyushee uravnenie dlya funkcii :

Poluchennoe uravnenie po vidu sovpadaet s uravneniem Shredingera dlya odnomernogo garmonicheskogo oscillyatora. Iz nerelyativistskoi kvantovoi mehaniki izvestno, chto sobstvennye funkcii takogo uravneniya obrashayutsya v nul' pri , kogda sobstvennye znacheniya proporcional'ny polozhitel'nym celym nechetnym chislam:

gde - celoe neotricatel'noe chislo. Sobstvennye funkcii, sootvetstvuyushie etim sobstvennym znacheniyam, imeyut vid:

gde - polinomy Ermita, a - normirovochnyi mnozhitel'. V itoge tochnye resheniya kvadrirovannogo uravneniya Diraka i sootvetstvuyushii im spektr energii mozhno zapisat' v vide:

gde vvedeny glavnoe kvantovoe chislo , numeruyushee energeticheskie urovni zaryazhennogo fermiona v magnitnom pole (urovni Landau) i prinimayushee celye neotricatel'nye znacheniya, i znak zaryada fermiona . Iz vyrazheniya dlya energii (2.14) sleduet, chto spektr energii fermiona imeet dvukratnoe vyrozhdenie po kvantovomu chislu pri i beskonechnokratnoe vyrozhdenie po chislu , esli ono nepreryvno.

Vospol'zuemsya uravneniem (2.4), chtoby po funkcii vosstanovit' funkciyu - tochnoe reshenie uravneniya Diraka v magnitnom pole. Raspishem yavno operator v vybrannoi nami sisteme koordinat i podeistvuem im na funkciyu iz (2.13), chto daet sleduyushee vyrazhenie dlya funkcii :

Sleduet napomnit', chto uravnenie po peremennoi  (2.10) formal'no sovpadaet s uravneniem Shredingera dlya garmonicheskogo oscillyatora. Poetomu po analogii s kvantovym oscillyatorom udobno vvesti povyshayushii i ponizhayushii operatory:

Napomnim deistvie operatorov na volnovuyu funkciyu oscillyatora:

Esli takzhe vvesti sleduyushie lineinye kombinacii -matric:

gde , - matricy Pauli, to funkciya privoditsya k vidu:

Pri takom podhode ostaetsya proizvol v vybore postoyannogo bispinora . Zafiksiruem etot proizvol, potrebovav, chtoby slagaemoe v formule (2.19) obratilos' v nul'. Vyberem bispinor vida:

kotoryi yavlyaetsya sobstvennoi funkciei operatora proekcii spina , a takzhe udovletvoryaet uravneniyu:

Iz etogo uravneniya sleduet, chto slagaemoe, proporcional'noe povyshayushemu operatoru, obrashaetsya v nul', esli . Poetomu pri takom vybore bispinora tochnoe reshenie uravneniya Diraka v postoyannom odnorodnom magnitnom pole mozhet byt' privedeno k vidu:

Osnovnym urovnem Landau estestvenno schitat' kvantovoe sostoyanie s , prichem vspomogatel'noe chislo , opredelyayushee nabor diskretnyh urovnei, takzhe ravno nulyu. Soglasno opredeleniyu energeticheskih urovnei (2.14) na osnovnom urovne sootnoshenie mezhdu energiei i impul'som ravno: , chto sootvetstvuet svobodnomu dvizheniyu zaryazhennogo fermiona vdol' osi . Pri etom volnovaya funkciya zaryazhennogo fermiona okazyvaetsya svyazannoi tol'ko s odnoi vspomogatel'noi funkciei sootnosheniem:

Posle podstanovki yavnogo vida funkcii  (2.13) normirovochnyi mnozhitel' opredelyaetsya iz usloviya:

gde integrirovanie provoditsya po ob'emu beskonechnogo (vdol' osi ) cilindra s poperechnym secheniem v vide pryamougol'nika so storonami i .

Otricatel'no chastotnoe reshenie mozhno poluchit' iz polozhitel'no chastotnogo (2.23) zamenami: , () i . V zaklyuchenie vypishem okonchatel'nyi rezul'tat dlya polozhitel'no i otricatel'no chastotnyh reshenii uravneniya Diraka zaryazhennogo fermiona, nahodyashegosya na osnovnom urovne Landau () vo vneshnem postoyannom odnorodnom magnitnom pole:

gde , - znak zaryada, - znak impul'sa vdol' napravleniya magnitnogo polya, - postoyannye spinory, opredelyaemye uravneniem (2.20). Sleduet takzhe zametit', chto bispinory normirovany usloviem tochno tak zhe, kak polozhitel'no i otricatel'no chastotnye resheniya svobodnogo uravneniya Diraka.

Zadanie 3. Naiti propagator elektrona v sil'nom magnitnom pole.

Reshenie. Magnitnoe pole estestvenno schitat' sil'nym, esli ono opredelyaet naibol'shii energeticheskii masshtab zadachi:

V etom sluchae elektrony budut nahodit'sya na osnovnom urovne Landau (), chto sushestvenno uproshaet zadachu o nahozhdenii propagatora elektrona v takom sil'nom magnitnom pole.

Na osnovnom urovne Landau elektron ( - znak zaryada fermiona) imeet sohranyayushuyusya proekciyu spina na napravlenie, protivopolozhnoe napryazhennosti magnitnogo polya, ( ) i, v sootvetstvii s (2.26), budet opisyvat'sya volnovoi funkciei vida:

gde - chisto polevoi parametr, i - energiya i impul's elektrona, prichem , - parametr s razmernost'yu massy, opredelyayushii polozhenie maksimuma volnovoi funkcii na osi , i - dliny normirovochnyh otrezkov vdol' osei i . Dlya vychisleniya propagatora naidem snachala matricu plotnosti . Iz kvantovoi teorii polya izvestno, chto dlya bispinora matrica plotnosti est':

gde 4-impul's i - vektor polyarizacii elektrona v ego sisteme pokoya. Uchityvaya v vybrannoi nami sisteme koordinat korrelyaciyu mezhdu spinom elektrona i napravleniem magnitnogo polya , vektor polyarizacii - , tak chto 4-vektor polyarizacii (3.4) svedetsya k . Podstavlyaya impul's i vektor polyarizacii v matricu plotnosti (3.3) i provodya prostye algebraicheskie preobrazovaniya, poluchim sleduyushii rezul'tat:

gde - operator proekcii spina fermiona na os' . Ispol'zuya opredelenie proekcionnogo operatora  (1.11), zapishem matricu plotnosti (3.5) v vide:

Dlya vychisleniya propagatora elektrona predstavim ego volnovuyu funkciyu v vide razlozheniya po operatoram rozhdeniya i unichtozheniya:

gde v polozhitel'no i otricatel'no chastotnyh resheniyah (3.2) pervye dva indeksa dlya kratkosti opusheny. Po opredeleniyu, propagator elektrona vychislyaetsya kak raznost' vremennogo i normal'nogo uporyadocheniya proizvedeniya i :

Prinimaya vo vnimanie svoistvo antikommutacii operatorov rozhdeniya i unichtozheniya elektrona, propagator elektrona (3.8) prinimaet vid:

gde i - vremennye komponenty 4-vektorov i . Pri vychislenii propagatora elektrona udobno pereiti ot summirovaniya k integrirovaniyu:

Podstavlyaya yavnyi vid funkcii  (3.2) v propagator (3.9), poluchim:

Sleduet zametit', chto pri vyvode propagatora v sluchae v integrale byla sdelana zamena peremennyh i . Dlya provedeniya dal'neishih preobrazovanii vospol'zuemsya sootnosheniem:

Delaya podstanovku etogo sootnosheniya v propagator (3.11), poluchim:

Integral po - gaussov i beretsya s pomosh'yu formuly:

V rezul'tate dlya propagatora elektrona poluchaetsya sleduyushee:

gde integrirovanie vedetsya v podprostranstve . Sleduet neskol'ko slov skazat' otnositel'no fazy  . Mozhno pokazat', chto ona mozhet byt' poluchena kak rezul'tat integrirovaniya po otrezku pryamoi , soedinyayushei tochki i chetyrehmernogo prostranstva-vremeni, tak chto . Vspomnim takzhe, chto reshenie uravneniya Diraka dlya elektrona naideno nami v kalibrovke 4-potenciala vneshnego polya vida: . Togda integral, vychislennyi po ukazannomu otrezku chetyrehmernogo prostranstva-vremeni:

s tochnost'yu do koefficienta svoditsya k (3.16). Poetomu fazu mozhno zapisat' v sleduyushem lorenc-invariantnom vide:

Faza, predstavlennaya v takoi forme, soderzhit neodnoznachnost', poskol'ku zavisit ot puti integrirovaniya. Chtoby izbavit'sya ot takoi zavisimosti, vmesto 4-potenciala vvedem novyi 4-vektor i potrebuem, chtoby on byl potencial'nym:

Ukazannogo svoistva mozhno dobit'sya, esli k potencialu dobavit' 4-vektor , gde - tenzor vneshnego postoyannogo elektromagnitnogo polya. Poetomu faza, zapisannaya v lorenc-invariantnom vide i ne zavisyashaya ot puti integrirovaniya, imeet vid:

V zaklyuchenie otmetim, chto nalichie etoi fazy v propagatore elektrona (3.15) delaet ego kalibrovochno i translyacionno neinvariantnym.

---

<< Titul'nyi list | Oglavlenie | Drevesnye processy >>

Publikacii s klyuchevymi slovami: kvantovaya teoriya polya - elementarnye chasticy - sverhsil'nye magnitnye polya - rozhdenie chastic Publikacii so slovami: kvantovaya teoriya polya - elementarnye chasticy - sverhsil'nye magnitnye polya - rozhdenie chastic
Sm. takzhe: Bozon Higgsa: ob'yasnenie v komikse Evolyuciya vselennoi Leptony Elementarnye chasticy Ee zvali Iks Pentakvark, opyat' pentakvark? Proton i antiproton: pohozhie ili odinakovye? Vse publikacii na tu zhe temu >>