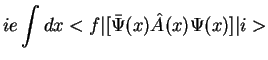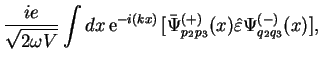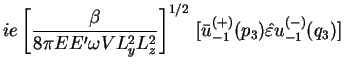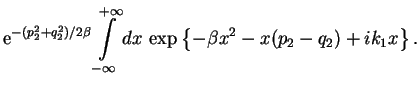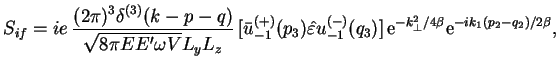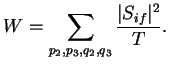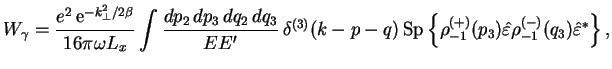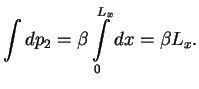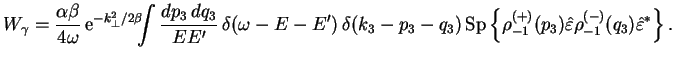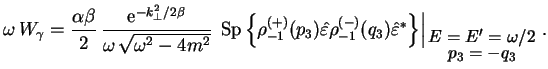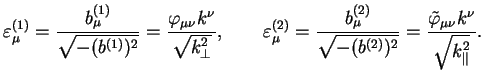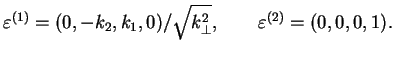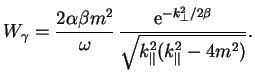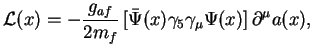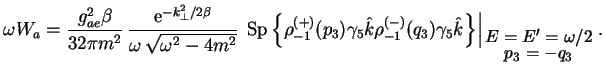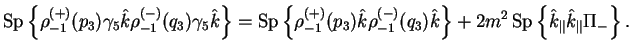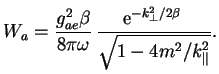<< Vvodnye zadaniya | Oglavlenie | Odnopetlevye dvuhtochechnye processy >>
Drevesnye processy
(Zadanie 4, Zadanie 5)
Zadanie 4. Vychislit' veroyatnost' raspada fotona na elektron-pozitronnuyu paru v sil'nom vneshnem magnitnom pole.
Reshenie. Raspad fotona na elektron-pozitronnuyu paru, zapreshennyi v vakuume zakonom sohraneniya energii-impul'sa, stanovitsya vozmozhnym v prisutstvii vneshnego magnitnogo polya. Eto svyazano s tem, chto magnitnoe pole vystupaet v roli aktivnoi vneshnei sredy, vzaimodeistvie s kotoroi privodit k izmeneniyu zakonov sohraneniya, a znachit, i kinematiki processa.
Poskol'ku raspad fotona analiziruetsya v predele sil'nogo magnitnogo
polya
![]() , gde
, gde ![]() - massa elektrona i
- massa elektrona i
![]() - energiya fotona, to estestvenno volnovye funkcii
elektrona i pozitrona vybrat' v asimptoticheskom vide (3.2).
Pereidem teper' k vychisleniyu
- energiya fotona, to estestvenno volnovye funkcii
elektrona i pozitrona vybrat' v asimptoticheskom vide (3.2).
Pereidem teper' k vychisleniyu ![]() -matrichnogo elementa processa
-matrichnogo elementa processa
![]() ,
izobrazhennogo diagrammoi na ris. 1.
,
izobrazhennogo diagrammoi na ris. 1.
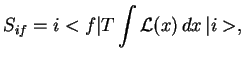 |
(4.1) |
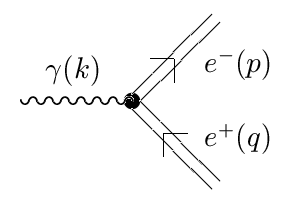 |
| Ris. 1. Diagramma, opisyvayushaya raspad fotona na elektron-pozitronnuyu paru vo vneshnem elektromagnitnom pole |
gde
gde
Integral po
gde pod trehmernoi
Veroyatnost' raspada fotona v edinicu vremeni ravna kvadratu modulya
![]() -matrichnogo elementa, otnesennogo k intervalu vremeni
-matrichnogo elementa, otnesennogo k intervalu vremeni ![]() ,
za kotoryi etot process proizoshel, i prosummirovannogo po vsevozmozhnym
konechnym sostoyaniyam:
,
za kotoryi etot process proizoshel, i prosummirovannogo po vsevozmozhnym
konechnym sostoyaniyam:
Kak i v sluchae propagatora elektrona, pri vychislenii veroyatnosti raspada
gde
Podstavlyaya etot integral v (4.6) i vvodya vmesto kvadrata zaryada postoyannuyu tonkoi struktury
Dve ostavshiesya
Pereidem k vychisleniyu shpura. Podstavlyaya yavnyi vid matric
![]() iz (3.6), dlya rassmatrivaemogo shpura
poluchim sleduyushii rezul'tat:
iz (3.6), dlya rassmatrivaemogo shpura
poluchim sleduyushii rezul'tat:
gde ispol'zovany svoistva (1.15) shpurov
Vyyasnim, fotony kakoi polyarizacii imeyut nenulevuyu veroyatnost' raspada
na elektron-pozitronnuyu paru. Dlya etogo vspomnim, chto tenzor napryazhennostei
vneshnego elektromagnitnogo polya pozvolyaet postroit' udobnyi
bazis (1.17) dlya takogo roda analiza. Pri etom dva
polyarizacionnyh sostoyaniya fotona, ortogonal'nyh k ego volnovomu vektoru
k, mogut byt' vybrany proporcional'nymi pervym dvum bazisnym
vektoram
![]() i
i
![]() :
:
V vybrannoi nami sisteme otscheta (
Tol'ko 4-vektor "vtoroi" fotonnoi polyarizacii imeet nenulevye sostavlyayushie v
Podstanovka
![]() iz (4.12) v vyrazhenie dlya
shpura (4.10) privodit k prostomu rezul'tatu -
iz (4.12) v vyrazhenie dlya
shpura (4.10) privodit k prostomu rezul'tatu - ![]() .
Uchityvaya, chto proizvedenie energii raspadayushegosya fotona na veroyatnost'
ego raspada est' lorenc-invariantnaya velichina, pereidem v proizvol'nuyu
sistemu otscheta (
.
Uchityvaya, chto proizvedenie energii raspadayushegosya fotona na veroyatnost'
ego raspada est' lorenc-invariantnaya velichina, pereidem v proizvol'nuyu
sistemu otscheta (
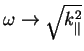 ) i dlya veroyatnosti raspada
) i dlya veroyatnosti raspada
![]() poluchim okonchatel'nyi rezul'tat:
poluchim okonchatel'nyi rezul'tat:
Zadanie 5. Vychislit' veroyatnost' raspada aksiona na elektron-pozitronnuyu paru v sil'nom vneshnem magnitnom pole.
Reshenie. Aksion - eto psevdoskalyarnaya chastica, vvedennaya dlya resheniya problemy CP-invariantnosti sil'nyh vzaimodeistvii. V modeli tak nazyvaemogo "nevidimogo" aksiona s pryamoi svyaz'yu aksiona s obychnymi fermionami lagranzhian vzaimodeistviya imeet vid:
gde
Raspad aksiona na elektron-pozitronnuyu paru, zapreshennyi v
vakuume zakonom sohraneniya energii-impul'sa, stanovitsya vozmozhnym v
prisutstvii vneshnego magnitnogo polya v polnoi analogii s raspadom fotona.
Legko uvidet', chto ![]() -matrichnyi element processa, izobrazhennogo na
ris. 2,
-matrichnyi element processa, izobrazhennogo na
ris. 2,
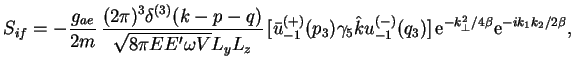 |
(5.2) |
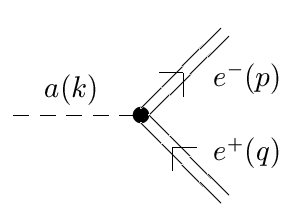 |
| Ris. 2. Diagramma, opisyvayushaya raspad aksiona na elektron-pozitronnuyu paru vo vneshnem elektromagnitnom pole v modeli s pryamoi svyaz'yu aksiona s elektronom |
gde
Vychislim shpur
Esli uchest', chto elektron i pozitron nahodyatsya na massovoi poverhnosti (
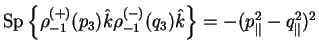 obrashaetsya v nul', a vtoroi -
obrashaetsya v nul', a vtoroi -
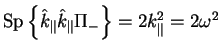 . Dalee, vozvrashayas' v proizvol'nuyu sistemu otscheta iz sistemy,
gde
. Dalee, vozvrashayas' v proizvol'nuyu sistemu otscheta iz sistemy,
gde
<< Vvodnye zadaniya | Oglavlenie | Odnopetlevye dvuhtochechnye processy >>
|
Publikacii s klyuchevymi slovami:
kvantovaya teoriya polya - elementarnye chasticy - sverhsil'nye magnitnye polya - rozhdenie chastic
Publikacii so slovami: kvantovaya teoriya polya - elementarnye chasticy - sverhsil'nye magnitnye polya - rozhdenie chastic | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |